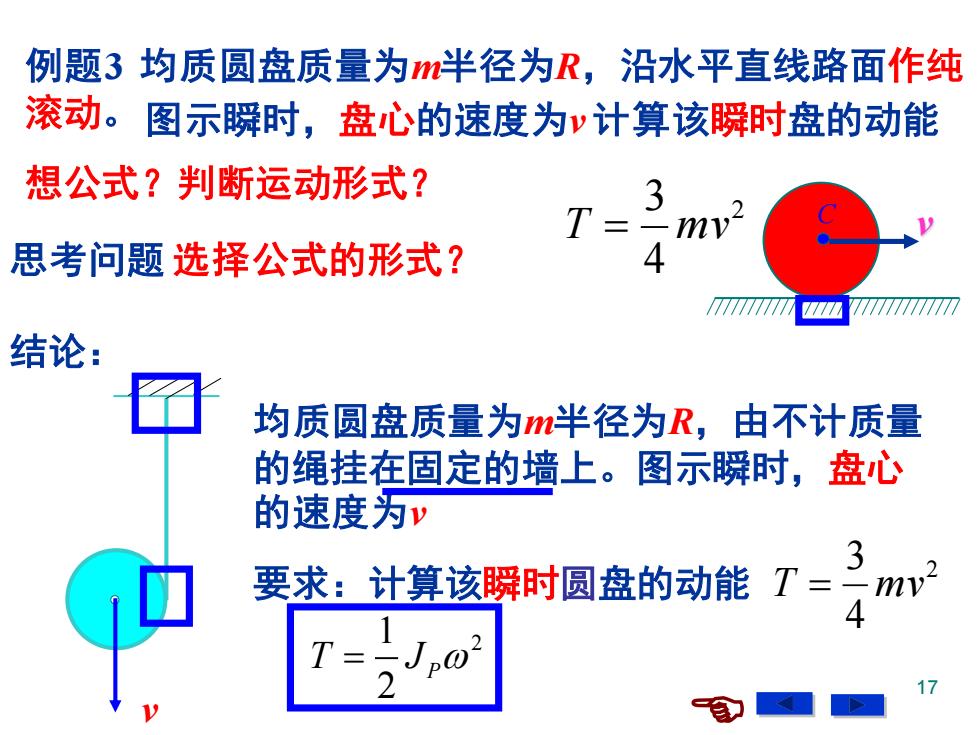
例题3均质圆盘质量为半径为R,沿水平直线路面作纯 滚动。图示瞬时,盘心的速度为v计算该瞬时盘的动能 想公式?判断运动形式? 思考问题选择公式的形式? 结论: 均质圆盘质量为m半径为R,由不计质量 的绳挂在固定的墙上。图示瞬时,盘心 的速度为v 3 要求:计算该瞬时圆盘的动能T=二mv 4 17
17 C v 例题3 均质圆盘质量为m半径为R,沿水平直线路面作纯 滚动。 想公式?判断运动形式? 思考问题 选择公式的形式? 结论: 图示瞬时,盘心的速度为v 计算该瞬时盘的动能 v 均质圆盘质量为m半径为R,由不计质量 的绳挂在固定的墙上。图示瞬时,盘心 的速度为v 要求:计算该瞬时圆盘的动能 2 4 3 T = mv 2 4 3 T = mv 1 2 2 T J = P

例题4铅直平面内的运动机构。定滑轮A动 A 滑轮B的质量m半径R,可看成均质圆盘; 物块D的质量为2m、E的质量为m 已知图示瞬时物块D向下运动的速度v 绳的质量不计不可伸长,绳与轮间无 相对滑动 T=25mv 25 16 要求:计算图示瞬时系统的动能 一看 系统由几部分组成? 再看 每一部分的运动形式如何? 三想想公式 想动滑轮B的动能如何计算?
18 例题4铅直平面内的运动机构。定滑轮A 动 滑轮B的质量m半径R,可看成均质圆盘; 物块D的质量为2m 、E 的质量为m 一看 系统由几部分组成? O D C A B 要求:计算图示瞬时系统的动能 v E 已知图示瞬时物块D向下运动的速度v 绳的质量不计不可伸长,绳与轮间无 相对滑动 再看 每一部分的运动形式如何? 三想 想公式 想动滑轮B的动能如何计算? 2 16 25 T = mv
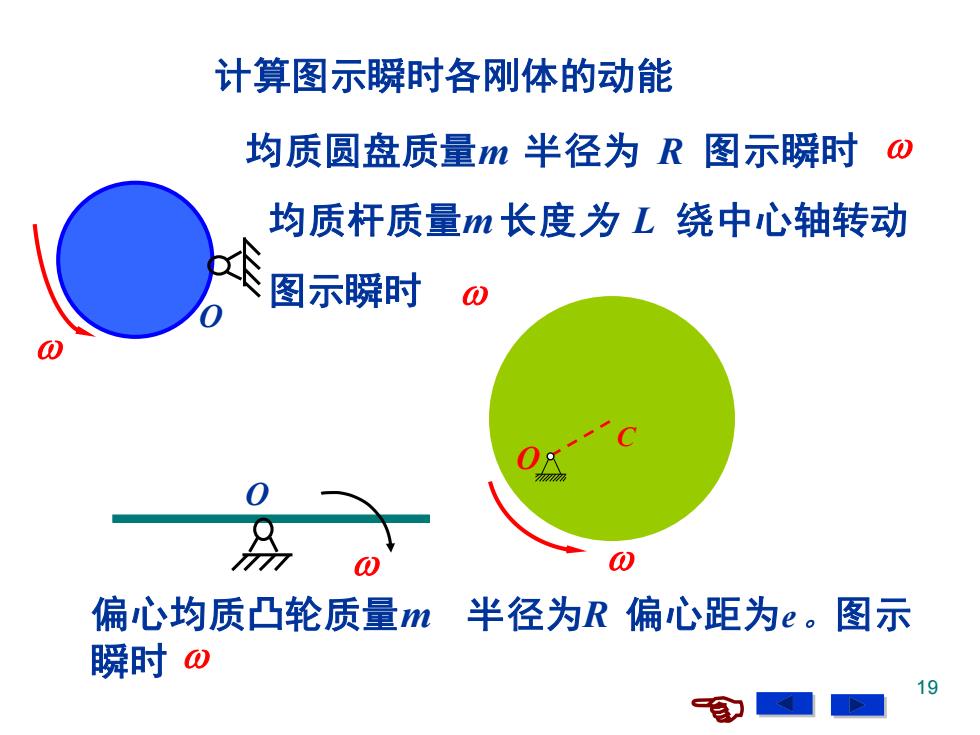
计算图示瞬时各刚体的动能 均质圆盘质量m半径为R图示瞬时ω 均质杆质量m长度为L绕中心轴转动 图示瞬时 偏心均质凸轮质量m半径为R偏心距为e。图示 瞬时o 19
19 均质圆盘质量m 半径为 R 图示瞬时 O C 均质杆质量m 长度为 L 绕中心轴转动 图示瞬时 偏心均质凸轮质量m 半径为R 偏心距为e 。图示 瞬时 计算图示瞬时各刚体的动能 O O
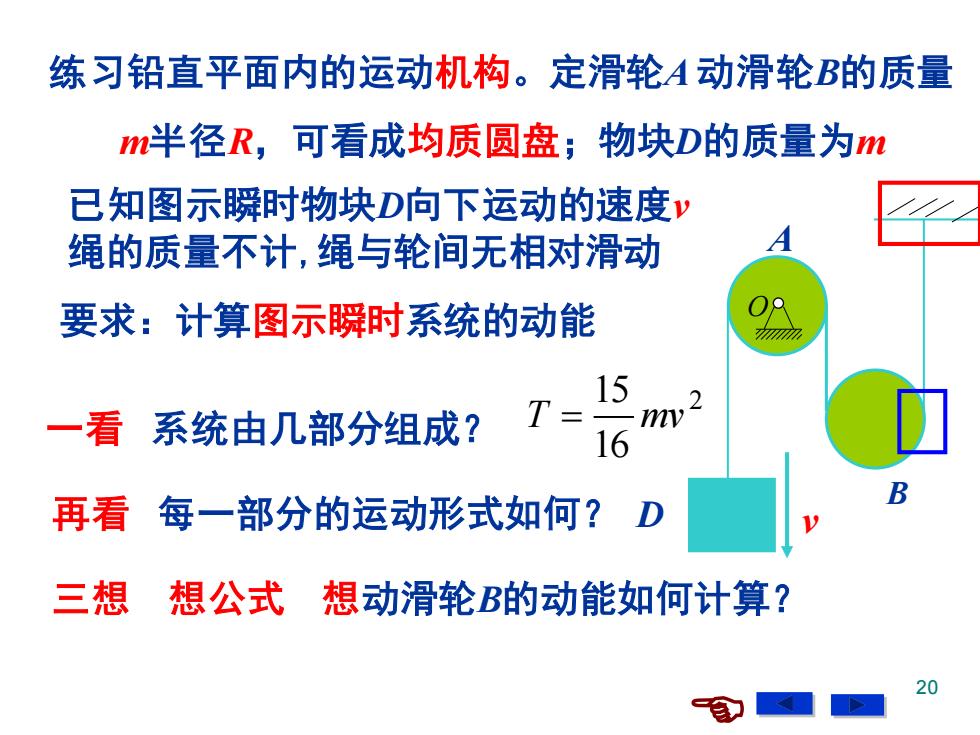
练习铅直平面内的运动机构。定滑轮A动滑轮B的质量 m半径R,可看成均质圆盘;物块D的质量为m 已知图示瞬时物块D向下运动的速度v 绳的质量不计,绳与轮间无相对滑动 要求:计算图示瞬时系统的动能 15 一看 系统由几部分组成? T= tc mv2 16 再看每一部分的运动形式如何? D 三想想公式想动滑轮B的动能如何计算? 20
20 练习铅直平面内的运动机构。定滑轮A 动滑轮B的质量 m半径R,可看成均质圆盘;物块D的质量为m O D A B v 要求:计算图示瞬时系统的动能 已知图示瞬时物块D向下运动的速度v 绳的质量不计,绳与轮间无相对滑动 一看 系统由几部分组成? 再看 每一部分的运动形式如何? 三想 想公式 想动滑轮B的动能如何计算? 2 16 15 T = mv

§12一2质点和质点系的动能 归纳总结 1计算刚体的动能和计算刚体的动量矩相类似, 必须要分析刚体的运动形式! 2 平移刚体的动能 定轴转动刚体的动能 平面运动刚体的动能 3对刚体系统而言凡是有质量又运动的物体必然有动能 4要用绝对的速度(角速度) 21
21 归纳总结 1 计算刚体的动能和计算刚体的动量矩相类似, 2 平移刚体的动能 定轴转动刚体的动能 平面运动刚体的动能 3 对刚体系统而言凡是有质量又运动的物体必然有动能 4 要用绝对的速度(角速度) §12-2质点和质点系的动能 必须要分析刚体的运动形式!