
§12一2质点和质点系的动能 质点的动能 瞬时值,是机械运动的另一种度量形式 质点系的动能 (一)一般表达式 T=∑m, (二)刚体的动能 (重点要求熟练掌握) 1平移刚体的动能 平移刚体的运动特点 T=Σm=Σm 可以和哪个 公式类比? 12 )
12 一 质点的动能 1 2 2 mv 二 质点系的动能 2 2 1 T = mi vi §12-2质点和质点系的动能 (一)一般表达式 瞬时值,是机械运动的另一种度量形式 1 平移刚体的动能 (二)刚体的动能(重点 要求熟练掌握) 平移刚体的运动特点 1 2 2 T m v = i i 1 2 2 C i = v m 1 2 2 = MvC 可以和哪个 公式类比?
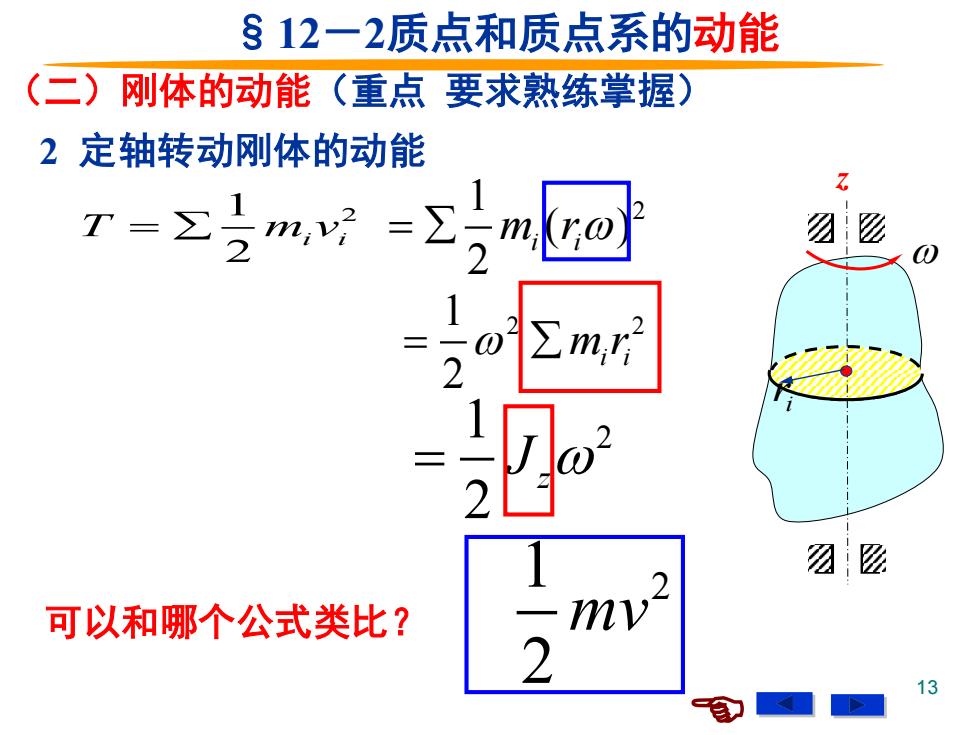
§12一2质点和质点系的动能 (二)刚体的动能(重点要求熟练掌握) 2定轴转动刚体的动能 1=Σ3mw2= ∑m,r ☑2 可以和哪个公式类比? 2 13
13 (二)刚体的动能(重点 要求熟练掌握) 2 定轴转动刚体的动能 1 2 2 T m v = i i 1 2 ( ) 2 = m r i i 1 2 2 2 = m ri i 可以和哪个公式类比? 1 2 2 z = J §12-2质点和质点系的动能 z i r 1 2 2 mv

§12一2质点和质点系的动能 (二)刚体的动能(重点要求熟练掌握) 3平面运动刚体的动能 T=Jp@2 为什么可以用 2 这个公式?? Jp=Jc+md T=,(Je+md)a2-2o 思考d.0=什么? +-Jc@2 思考问题1:将上述公式改为对任意点是否可以? 思考问题2:如何选择上述两个公式?
14 3 平面运动刚体的动能 1 2 2 T J = P JP=JC + md 2 1 2 2 ( ) 2 T J md = + C 思考 d. =什么? 2 2 2 1 2 1 T = mvC + JC C P 为什么可以用 这个公式?? 思考问题1 :将上述公式改为对任意点是否可以? 思考问题2:如何选择上述两个公式? 1 1 2 2 ( ) 2 2 C = + J m d §12-2质点和质点系的动能 (二)刚体的动能(重点 要求熟练掌握)
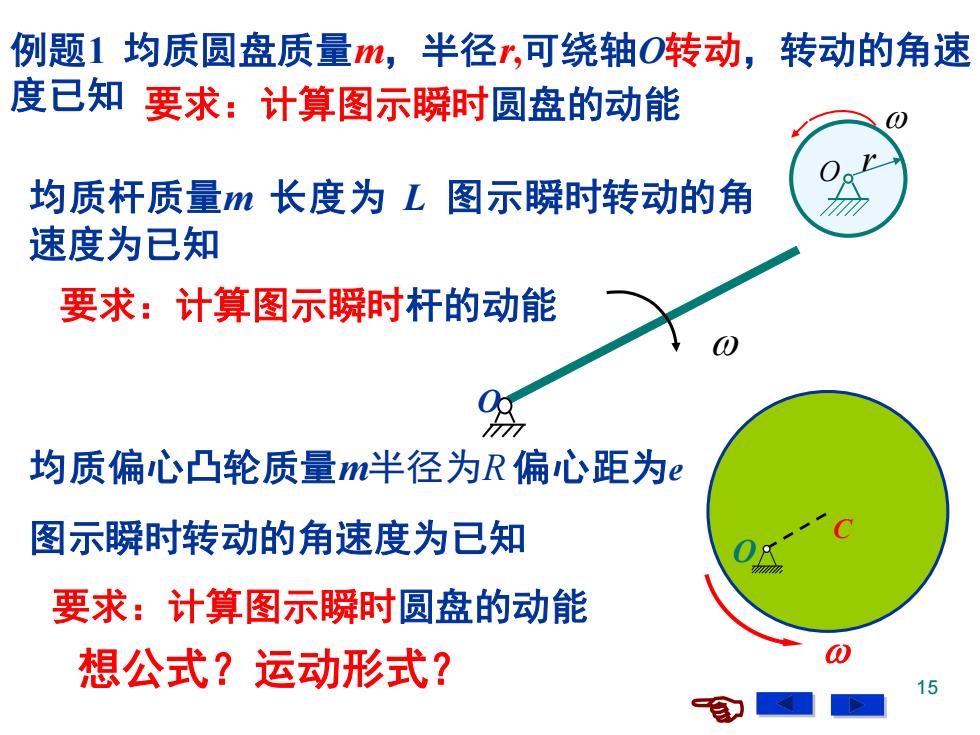
例题1均质圆盘质量m,半径r,可绕轴O转动,转动的角速 度已知要求:计算图示瞬时圆盘的动能 均质杆质量m长度为L图示瞬时转动的角 速度为已知 要求:计算图示瞬时杆的动能 均质偏心凸轮质量m半径为R偏心距为e 图示瞬时转动的角速度为已知 要求:计算图示瞬时圆盘的动能 想公式?运动形式? 15
15 r O 例题1 均质圆盘质量m,半径r,可绕轴O转动,转动的角速 度已知 要求:计算图示瞬时圆盘的动能 均质杆质量m 长度为 L 图示瞬时转动的角 速度为已知 要求:计算图示瞬时杆的动能 O C 均质偏心凸轮质量m半径为R 偏心距为e 图示瞬时转动的角速度为已知 要求:计算图示瞬时圆盘的动能 想公式?运动形式? O

例题2均质圆盘质量m,半径r,可绕轴O转动,角速度为o 其上缠有一质量不计的绳,重物A 的质量为m,并设绳不可伸长且与圆盘间无 相对滑动 要求:计算图示瞬时系统的动能 A T-mroi+-(mr)o-3mo
16 r O A 例题2 均质圆盘质量m,半径r,可绕轴O转动,角速度为 要求:计算图示瞬时系统的动能 其上缠有一质量不计的绳,重物A 的质量为m,并设绳不可伸长且与圆盘间无 相对滑动 2 2 2 2 2 2 4 3 ) 2 1 ( 2 1 2 1 T = m r + m r = m r