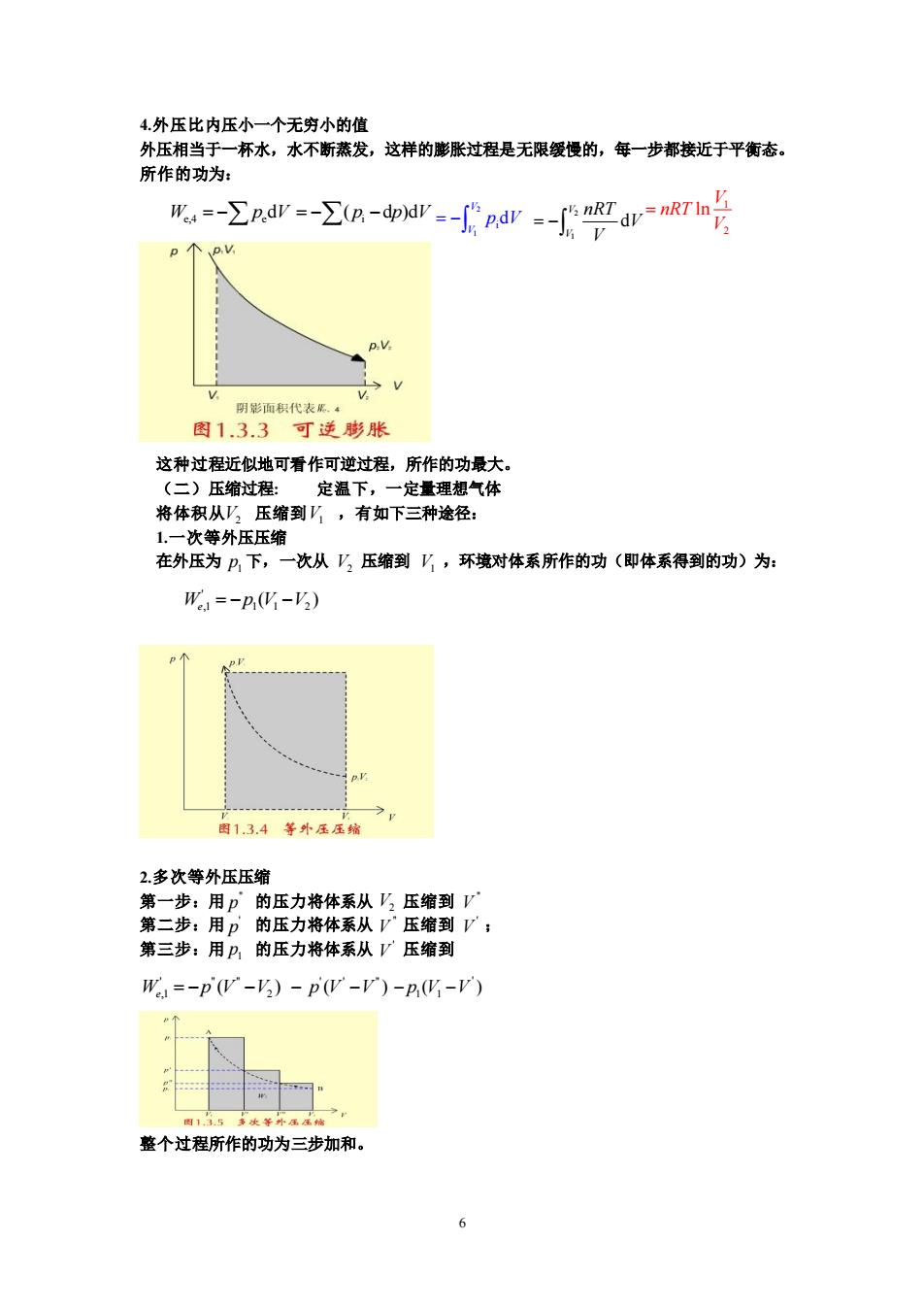
4.外压比内压小一个无穷小的值 外压相当于一杯水,水不断蒸发,这样的膨胀过程是无限缓慢的,每一步都接近于平衡态 所作的功为: Σdr-a-r:-nr-fgan号 个0 面积代表网 图1.3.3可逆膨胀 这种过程近似地可看作可逆过程,所作的功最大。 (一)压缩过程: 定温下,一定量理想气体 将体积从压缩到八,有如下三种途径: 1,一次等外压压缩 在外压为户下,一次从乃压缩到,环境对体系所作的功(即体系得到的功)为: W=-p,(化-) 图13.4等外压压% 2.多次等外压压缩 第一步:用p的压力将体系从压缩到y 第二步:用 的压力将体系从V压缩到V; 第三步:用户的压力将体系从压缩到 W=-pV-2)-pW-V)-p化-V 画5淡等本堡之 整个过程所作的功为三步加和。 6
6 4.外压比内压小一个无穷小的值 外压相当于一杯水,水不断蒸发,这样的膨胀过程是无限缓慢的,每一步都接近于平衡态。 所作的功为: 这种过程近似地可看作可逆过程,所作的功最大。 (二)压缩过程: 定温下,一定量理想气体 将体积从 压缩到 ,有如下三种途径: 1.一次等外压压缩 在外压为 下,一次从 压缩到 ,环境对体系所作的功(即体系得到的功)为: 2.多次等外压压缩 第一步:用 的压力将体系从 压缩到 第二步:用 的压力将体系从 压缩到 ; 第三步:用 的压力将体系从 压缩到 整个过程所作的功为三步加和。 W p V e,4 e = − d i = − − ( d )d p p V 2 1 id V V = − p V 2 1 d V V nRT V V = − 1 2 ln V nRT V = V2 V1 1 p V2 V1 ' ,1 1 1 2 ( ) W p V V e = − − " p V2 " V ' p " V ' V 1 p ' V ' " " ,1 2 ( ) W p V V e = − − ' ' " ( ) − − p V V ' 1 1 − − p V V ( )
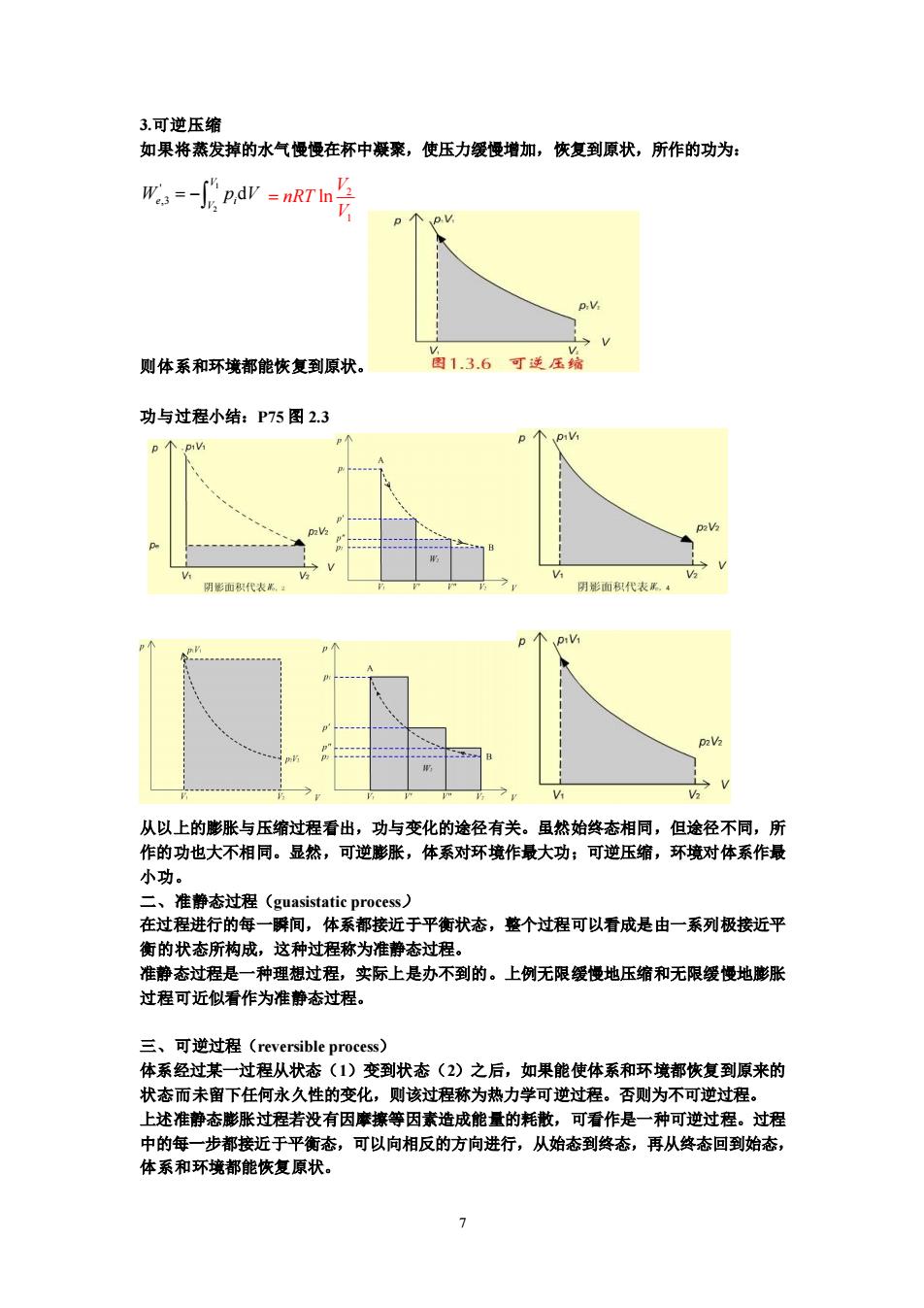
3.可逆压缩 如果将蒸发掉的水气慢慢在杯中凝聚,使压力缓慢增加,恢复到原状,所作的功为: ges=-fpdr=nRrn点 则体系和环境都能恢复到原状。 图1.3.6可逆压 功与过程小结:P75图2.3 p个p的 阴面积代表 从以上的膨胀与压缩过程看出,功与变化的途径有关。虽然始终态相同,但途径不同,所 作的功也大不相同。显然,可逆膨胀,体系对环境作最大功;可逆压缩,环境对体系作最 小功。 二、准静态过程(guasistatic process) 在过程进行的每一瞬间,体系都接近于平衡状态,整个过程可以看成是由一系列极接近平 衡的状态所构成,这种过程称为准静态过程 准静态过程是一种理想过程,实际上是办不到的。上例无限缓慢地压缩和无限缓慢地膨胀 过程可近似看作为准静态过程。 三、可逆过程(reversible process)? 体系经过其 过程从状态(1)变到状态(2)之后,如果能使体系和环境都恢复到原来的 状态而未留下任何水久性的变化,则该过程称为热力学可逆过程。否则为不可逆过程 上述准静态膨胀过程若没有因摩赛等因素造成能量的耗散,可看作是一种可逆过程。过程 中的每一步都接近于平衡态,可以向相反的方向进行,从始态到终态,再从终态回到始态, 体系和环境都能恢复原状
7 3.可逆压缩 如果将蒸发掉的水气慢慢在杯中凝聚,使压力缓慢增加,恢复到原状,所作的功为: 则体系和环境都能恢复到原状。 功与过程小结:P75 图 2.3 从以上的膨胀与压缩过程看出,功与变化的途径有关。虽然始终态相同,但途径不同,所 作的功也大不相同。显然,可逆膨胀,体系对环境作最大功;可逆压缩,环境对体系作最 小功。 二、准静态过程(guasistatic process) 在过程进行的每一瞬间,体系都接近于平衡状态,整个过程可以看成是由一系列极接近平 衡的状态所构成,这种过程称为准静态过程。 准静态过程是一种理想过程,实际上是办不到的。上例无限缓慢地压缩和无限缓慢地膨胀 过程可近似看作为准静态过程。 三、可逆过程(reversible process) 体系经过某一过程从状态(1)变到状态(2)之后,如果能使体系和环境都恢复到原来的 状态而未留下任何永久性的变化,则该过程称为热力学可逆过程。否则为不可逆过程。 上述准静态膨胀过程若没有因摩擦等因素造成能量的耗散,可看作是一种可逆过程。过程 中的每一步都接近于平衡态,可以向相反的方向进行,从始态到终态,再从终态回到始态, 体系和环境都能恢复原状。 1 2 ' ,3 d V e i V W p V = − 2 1 ln V nRT V =

2.6格(enthalpy) 1.焙的定义式 H=U+pV 2为什么要定义格? 为了使用方便,因为在等压、不作非膨胀功的条件下,培变等于等压热效应。容 易测定,从而可求其它热力学函数的变化值 即Q-DH (封闭系统 等压,W'=0) 3焙是状态函数定义式中培由状态函数组成。 4注意:培不是能量虽然具有能量的单位,但不遵守能量守恒定律。 2.7热容(heat capacity) 对于组成不变的均相封闭体系,不考虑非膨张功,设体系吸热,温度从1升高到 2,则: 1.平均热容 定义 <C>T;-T 单位 J.K-1 C=0O (温度变化很 2.比热容: 规定物质的数量为1g(或1kg)的热容。 它的单位是JK1.g或JK-1kg 3.摩尔热容Cm 规定物质的数量为1m0l的热容。 单位为:J.K-.mol- 4等压热帝C,9=(册。 dT △H=Qp=[CdT 海#海aG品-( 6.热容与温度的关系: 热容与温度的函数关系因物质、物态和温度区间的不同而有不同的形式。例如,气体的等压 摩尔热容与T的关系有如下经验式:
8 2.6 焓 (enthalpy) 1.焓的定义式: H = U + pV 2.为什么要定义焓? 为了使用方便,因为在等压、不作非膨胀功的条件下,焓变等于等压热效应 。 容 易测定,从而可求其它热力学函数的变化值 即 Qp=DH 或 dQp=dH (封闭系统,等压,W ' = 0) 3.焓是状态函数 定义式中焓由状态函数组成。 4.注意: 焓不是能量 虽然具有能量的单位,但不遵守能量守恒定律。 2.7 热容 (heat capacity) 对于组成不变的均相封闭体系,不考虑非膨胀功,设体系吸热 Q,温度从 T1 升高到 T2,则: 1.平均热容 定义 单位 (温度变化很小) 2.比热容: 规定物质的数量为 1 g(或 1 kg)的热容。 它的单位是 或 。 3.摩尔热容 Cm: 规定物质的数量为 1 mol 的热容。 单位为: 4.等压热容 Cp: 5.等容热容 Cv: 6.热容与温度的关系: 热容与温度的函数关系因物质、物态和温度区间的不同而有不同的形式。例如,气体的等压 摩尔热容与 T 的关系有如下经验式: T2 T1 Q C − = 1 J K − d Q C T = 1 1 J K g − − 1 1 J K kg − − 1 1 J K mol − − ( ) d p p p Q H C T T = = = = H Q C T p pd ( ) d V V V Q U C T T = = ( ) d V V V Q U C T T = =

Cp.m=a+bT+cT2+.或 Cpm=a'+b'T+c'T+. 式中a,b,ca是经验常数,由各种物质本身的特性决定,可从热力学数据表中查找。 2.8热力学第一定律对理想气体的应用 本节主婴介绍以下3个问 1盖昌萨克一焦耳实验(理 想气体的U和HD 2理想气体的印与C之差 3绝热过程方程式和过程的功 c-Joule实验(理想气体的U和H) 焦耳在184 别做了如下实验 将两个容量相等的容器,放在水浴中,左球充满气体,右球为真空(如图所示)。 打开活塞,气体由左球冲入右球,达平衡(如图所示) 水浴温度没有变化,即Q=0:由于体系的体积取两个球的总和,所以体系没有对外做功, W=0:根据热力学第一定律得该过程的△U=0 气达到平 盖.吕萨克-焦耳实脸(1) 盖昌蓝克-焦耳卖给(2》 Gay-Lussac-Joule实验一结论 前述:对于定量的纯物质,热力学能U由P,V,T中的任意两个独立变量来确定: 设热力学能可写成0f(T,) 微分 -()V( 焦耳实验结果:d7=0,dU=0,d≠0 dT-0,d≠0 0 同理,若内能写成 0=f(T,p) 9
9 或 式中 a,b,c,a’,. 是经验常数,由各种物质本身的特性决定,可从热力学数据表中查找。 2.8 热力学第一定律对理想气体的应用 本节主要介绍以下 3 个问题: 1.盖•吕萨克—焦耳实验(理想气体的 U 和 H) 2.理想气体的 Cp 与 Cv 之差 3.绝热过程方程式和过程的功 1. Gay-Lussac-Joule 实验(理想气体的 U 和 H) 盖•吕萨克 1807 年,焦耳在 1843 年分别做了如下实验: 将两个容量相等的容器,放在水浴中,左球充满气体,右球为真空(如图所示)。 打开活塞,气体由左球冲入右球,达平衡(如图所示) 水浴温度没有变化,即 Q=0;由于体系的体积取两个球的总和,所以体系没有对外做功, W=0;根据热力学第一定律得该过程的 。 Gay-Lussac-Joule 实验—结论 前述:对于定量的纯物质,热力学能 U 由 P,V,T 中的任意两个独立变量来确定: 设热力学能可写成 U=f(T,V) 微分 焦耳实验结果:dT=0,dU=0,dV≠0 dT=0,dV≠0 同理,若内能写成 U = f(T,p) 2 C a bT cT p,m = + + + 1 2 ,m ' ' ' C a b T c T p − − = + + + T V U U dU = ( ) dV + ( ) dT V T T V U U 0= ( ) dV + ( ) dT V T T U ( ) =0 V T U ( ) =0 P = U 0

常温常压时的气体可视为理想气体 故:理想气体的内能仅是温度的函数,与体积或压力无关,即可(T) 对于理想气体,在等温条件下PV-常数,即PV)0,所以根据格的定义可证理想气体的 枯也仅为温度的函数。 即 H=H(T) 0,=0学-0 周为G=C,=欲。 故:理想气体的Cy,C也仅为温度的函数。 本节小结:从盖吕萨克一焦耳实验得到理想气体的热力学能和烙仅是温度的函数,用数学 表示为: 0-0(0-0U=tm (0,=00=0H=im 即:在恒温时,改变体积或压力,理想气体的热力学能和培保持不变。且理想气体的C,Cp 也仅为温度的函数。 2.理想气体的Cp与Cv之差 气体的C印恒大于C: 因为等容过程中,升高温度,体系所吸的热全部用来增加热力学能:而等压过程中,所吸 的热除增加热力学能外,还要多吸一点热量用来对外做影胀功,所以气体的C印恒大于C,。 对于理想气体:Cp-Cy=nR Cpm-Cym=R(下面证明) 一般封闭体系Cp与Cv之差 C,-=0,- -aP),-(代入院义式) T =,+,a 下面需要证明 书P454附录:根据复合函数的偏微商公式可证 证明设:
10 常温常压时的气体可视为理想气体 故:理想气体的内能仅是温度的函数,与体积或压力无关,即 U=f(T) 对于理想气体,在等温条件下 PV=常数,即 d(PV)=0,所以根据焓的定义可证理想气体的 焓也仅为温度的函数。 即 又因为 故:理想气体的 Cv,Cp 也仅为温度的函数。 本节小结:从盖•吕萨克—焦耳实验得到理想气体的热力学能和焓仅是温度的函数,用数学 表示为: 即:在恒温时,改变体积或压力,理想气体的热力学能和焓保持不变。且理想气体的 Cv,Cp 也仅为温度的函数。 2. 理想气体的 Cp 与 Cv 之差 气体的 Cp 恒大于 Cv: 因为等容过程中,升高温度,体系所吸的热全部用来增加热力学能;而等压过程中,所吸 的热除增加热力学能外,还要多吸一点热量用来对外做膨胀功,所以气体的 Cp 恒大于 Cv 。 对于理想气体: (下面证明) 一般封闭体系 Cp 与 Cv 之差 (1 式) 下面需要证明 书 P454 附录:根据复合函数的偏微商公式可证 证明 设: H H T = ( ) ( ) 0 T H V = ( ) 0 T H p = ( ) V V U C T = ( ) p p H C T = ( ) 0 T U V = ( ) 0 T U p = U U T = ( ) ( ) 0 T H V = ( ) 0 T H p = H H T = ( ) C C nR p V − = C C R p,m V,m − = ( ) ( ) p p V V H U C C T T − = − ( ) ( ) ( ) p V U PV U H T T + = − (代入 定义式) ( ) ( ) ( ) p p V V U p T U T T = + − ( ) ? p U T =