
1.10洛仑兹引理 A(B×C)=B.(C×)=C.(A×B) en×E,=en×E2=0 0 f(花xi,×)-i iJm—JEJ-EJ2)d亚 Jml=Jm2 =0 =0 J2(2) Je() →E2·J()=E·J2() 导波场论 6
1.10洛仑兹引理 导波场论 en E1 en E2 0 Jm1 Jm2 0 1 2 2 1 1 m2 2 m1 2 e1 1 e2 E H E H dS H J H J E J E J dV 0 A(BC) B(C A) C (A B) 0 E2 Je1 r1 =E1 Je2 r2 6

1.10洛仑滋引理 E2·Je()=E1·J2(2) 口物理含义:说明e1(r1)在r2处激起的电场E12)与2 处的激励电流J22)的点乘,等于Je2(2)在r1处激起的 电场E2)与r1处的激动电流Jc1c)的点乘。 口这个结论与电路理论的互易定理相似。这个结果 是说系统的响应E,E,不会因为源点和场点的交 换而改变。 导波场论 7
1.10洛仑兹引理 p 物理含义:说明Je1 (r1)在r2处激起的电场E1 (r2 )与r2 处的激励电流Je2 (r2 )的点乘,等于Je2 (r2 )在r1处激起的 电场E2 (r1 )与r1处的激励电流Je1 (r1 )的点乘。 p 这个结论与电路理论的互易定理相似。这个结果 是说系统的响应 不会因为源点和场点的交 换而改变。 导波场论 E2 Je1 r1 =E1 Je2 r2 1 2 E , E 7
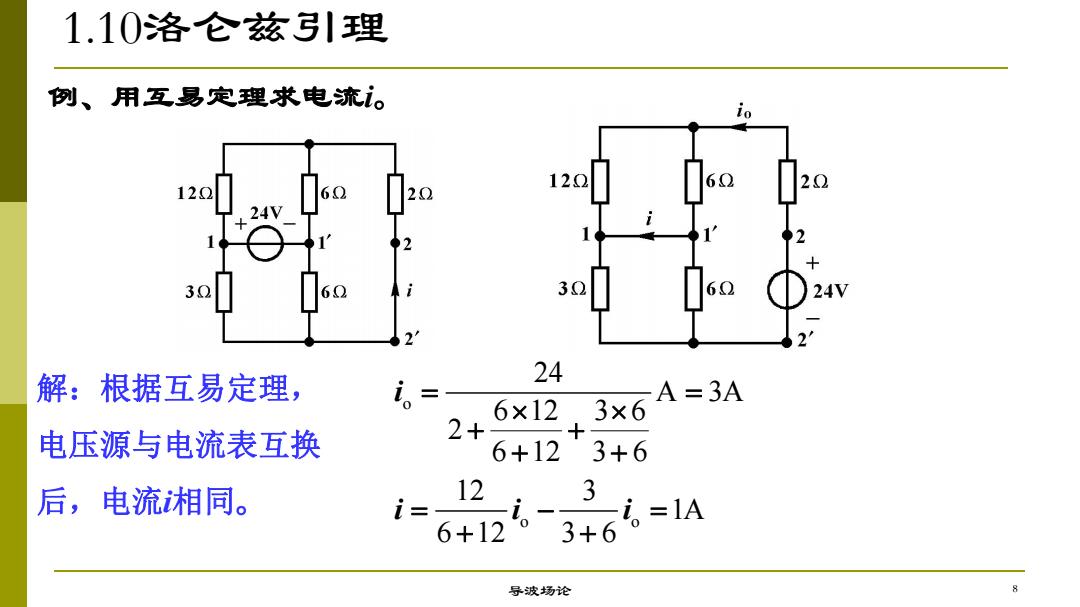
1.10洛仑兹引理 例、用互易定理求电流。 io 120 24V 30 解:根据互易定理, 24 i 6×123×6 A=3A 电压源与电流表互换 2+ 6+123+6 后,电流湘同。 12 3 i= 6+12.3+6 i。=lA 导波场论
例、用互易定理求电流i。 o o o 24 A 3A 6 12 3 6 2 6 12 3 6 12 3 1A 6 12 3 6 i i i i 解:根据互易定理, 电压源与电流表互换 后,电流i相同。 1.10洛仑兹引理 导波场论 8

1.10洛仑兹引理 口第三种情况S为无限远处的球面 由于$处的场极其远离源,因而可以局域地考虑成平面波。利 用电场与兹场之间的阻抗关系,得 (E×H2-E2×H1)e =(en×E)H2-(en×E2)H1 H-H,-H2H,=0 7 17 口与S为理想导体的结论一致。 ▣问题:为什么把电路的互易放在第二种情况下? 导波场论
导波场论 p 第三种情况S为无限远处的球面 由于S处的场极其远离源,因而可以局域地考虑成平面波。利 用电场与磁场之间的阻抗关系,得 1.10洛仑兹引理 1 2 2 1 1 2 2 1 1 2 2 1 1 1 0 n n n E H E H e e E H e E H H H H H p 与S为理想导体的结论一致。 p 问题:为什么把电路的互易放在第二种情况下? 9