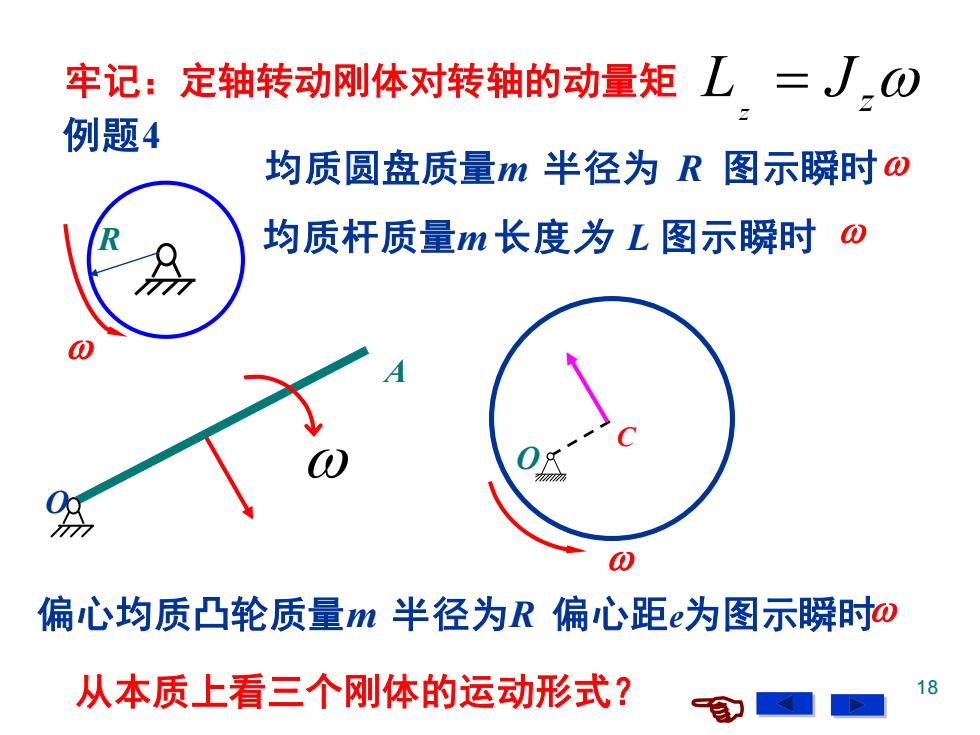
牢记:定轴转动刚体对转轴的动量矩L=了0 例题4 均质圆盘质量m半径为R图示瞬时ω 均质杆质量m长度为L图示瞬时ω A 0 偏心均质凸轮质量m半径为R偏心距e为图示瞬时o 从本质上看三个刚体的运动形式? 18
18 均质圆盘质量m 半径为 R 图示瞬时 R O C 均质杆质量m 长度为 L 图示瞬时 偏心均质凸轮质量m 半径为R 偏心距e为图示瞬时 从本质上看三个刚体的运动形式? 牢记:定轴转动刚体对转轴的动量矩 L J z z = O A 例题4

§11一1质点和质点系的动量矩 归纳总结 ·质点的动量矩如何计算? 名 ÷刚体的动量矩如何计算? 冬 19
19 归纳总结 ❖ 质点的动量矩如何计算? ❖ ❖ 刚体的动量矩如何计算? ❖ §11-1 质点和质点系的动量矩

本次课的教学目标 2会计算刚体的动量矩? 迁移了吗? 20
20 本次课的教学目标 2 会计算刚体的动量矩? 迁移了吗?
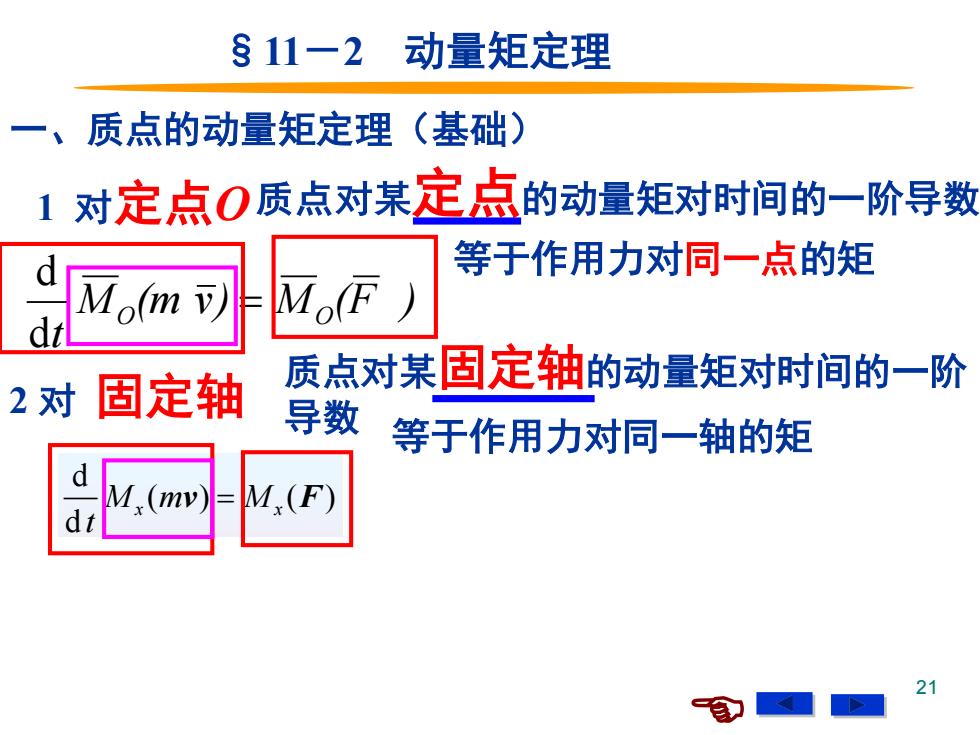
§11-2 动量矩定理 一、 质点的动量矩定理(基础) 1对定点0质点对某定点的动量矩对时间的一阶导数 等于作用力对同一点的矩 M,m可 2对 固定轴 质点对某固定轴的动量矩对时间的一阶 导数 等于作用力对同一轴的矩 M,(mv M (F) 21
21 质点对某定点的动量矩对时间的一阶导数, §11-2 动量矩定理 1 对定点O 一、质点的动量矩定理(基础) 等于作用力对同一点的矩 2 对 固定轴 质点对某固定轴的动量矩对时间的一阶 导数 等于作用力对同一轴的矩 d ( ) ( ) d d ( ) ( ) d d ( ) ( ) d x x y y z z M m M t M m M t M m M t = = = v F v F v F M (m v) M (F ) t O = O d d

§11一2动量矩定理 二、 质点系的动量矩定理(联想 d 1 固定点O o(m)=Mo(F t Mo(mv,) -Mo(F")+ M瓦) 质点系对固定点的动量矩定理为: ∑MF0)=0 M.(mV 22
22 二、质点系的动量矩定理(联想) M (m v ) M (F ) M (F ) t (e) O i (i) O i i = O i + d d M (m v ) M (F ) M (F ) t (e) O i (i) O i i = O i + d d 质点系对固定点的动量矩定理为: MO (Fi (i) ) = 0 t L M (m v ) t M (m v ) t O O i i O i i d d d d d d = = 1 固定点O §11-2 动量矩定理 M ( m v) M (F ) t O = O d d =