西北农林科技大学：《食品试验设计优化》课程教学资源（PPT课件）第十二章 回归设计

12.1.2 多元线性回归 (12.1.1)是一个多项式回归模型，在对变量作了变换并重新 命名后也可以看成是一个多元线性回归模型。 1．回归模型 设所收集到的n组数据为 假定回归模型为： (xi1 , xi2 ,  , xi p , yi ), i = 1,2,  ,n (7.1.5) ~ (0, ) 1,2, , 2 0 1 1    = + + + + =       iid N y x x i n i i i p i p i 各  ， 

12.1.2 多元线性回归 (12.1.1)是一个多项式回归模型，在对变量作了变换并重新 命名后也可以看成是一个多元线性回归模型。 1．回归模型 设所收集到的n组数据为 假定回归模型为： (xi1 , xi2 ,  , xi p , yi ), i = 1,2,  ,n (7.1.5) ~ (0, ) 1,2, , 2 0 1 1    = + + + + =       iid N y x x i n i i i p i p i 各  ， 

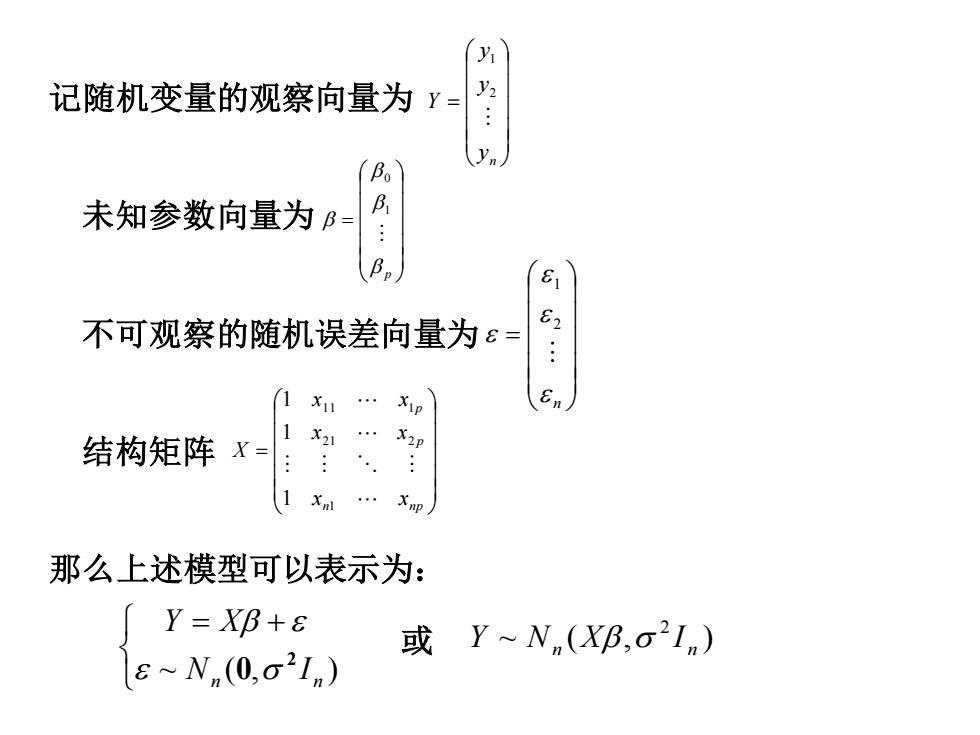
记随机变量的观察向量为 未知参数向量为 不可观察的随机误差向量为 结构矩阵 那么上述模型可以表示为：               = n y y y Y  2 1               =  p     1 0               = n      2 1               = n np p p x x x x x x X        1 21 2 11 1 1 1 1    = + ~ ( , ) n n N I Y X 2  0    或 ~ ( , ) 2 n n Y N X  I

记随机变量的观察向量为 未知参数向量为 不可观察的随机误差向量为 结构矩阵 那么上述模型可以表示为：               = n y y y Y  2 1               =  p     1 0               = n      2 1               = n np p p x x x x x x X        1 21 2 11 1 1 1 1    = + ~ ( , ) n n N I Y X 2  0    或 ~ ( , ) 2 n n Y N X  I

2．回归系数的最小二乘估计 估计回归模型中回归系数的方法是最小二乘法。 记回归系数的最小二乘估计（LSE）为 ， 应满足如下正规方程组： 当 存在时，最小二乘估计为 在求得了最小二乘估计后，可以写出回归方程： 今后称 为正规方程组的系数矩阵， 为正规 方程组的常数项向量， 为相关矩阵。 在模型（12.1.5）下，有 ( , , , ) 0 1 =  b b b  bp XXb = XY ( ) −1 X X b = (X X ) X Y −1 p p y = b + b x ++ b x 0 1 1 ˆ A = X X B = X Y ( ) −1 C = X X ~ ( , ( ) ) 2 −1 b N   XX

2．回归系数的最小二乘估计 估计回归模型中回归系数的方法是最小二乘法。 记回归系数的最小二乘估计（LSE）为 ， 应满足如下正规方程组： 当 存在时，最小二乘估计为 在求得了最小二乘估计后，可以写出回归方程： 今后称 为正规方程组的系数矩阵， 为正规 方程组的常数项向量， 为相关矩阵。 在模型（12.1.5）下，有 ( , , , ) 0 1 =  b b b  bp XXb = XY ( ) −1 X X b = (X X ) X Y −1 p p y = b + b x ++ b x 0 1 1 ˆ A = X X B = X Y ( ) −1 C = X X ~ ( , ( ) ) 2 −1 b N   XX

若记 C = (X X ) −1 = (cij) ，那么 bj ~ N( j ,cjj ), j 0,1,2, , p   2 =  在通常的回归分析中，由于C非对角阵，所以各回归系数间 是相关的： 2 Cov(bi ,bj ) = cij

若记 C = (X X ) −1 = (cij) ，那么 bj ~ N( j ,cjj ), j 0,1,2, , p   2 =  在通常的回归分析中，由于C非对角阵，所以各回归系数间 是相关的： 2 Cov(bi ,bj ) = cij

3．对回归方程的显著性检验 对回归方程的显著性检验是指检验如下假设： H0： H1： 不全为0 检验方法是作方差分析。 记 则有平方和分解式 其中 为残差平方和，自由度为 为回归平方和，自由度为 当H0为真时，有 对于给定的显著性水平 ，拒绝域为 。 1 =  2 =  =  p = 0    p , , , 1 2  y ˆ i = b0 + b1 xi1 ++ bp xi p，i = 1,2,  ,n E R n i i n i i i n i ST =  yi − y =  y − y + y − y = S + S = = =1 2 1 2 1 2 ( ) ( ˆ ) ( ˆ ) =  − i E i i S y y 2 ( ˆ ) f E = n − p −1 = − 2 S (y ˆ y) R i f R = p ~ ( , ) ( , 1) / / = F f f = F p n − p − S f S f F R E E E R R  ( , 1) F  F1− p n − p −

3．对回归方程的显著性检验 对回归方程的显著性检验是指检验如下假设： H0： H1： 不全为0 检验方法是作方差分析。 记 则有平方和分解式 其中 为残差平方和，自由度为 为回归平方和，自由度为 当H0为真时，有 对于给定的显著性水平 ，拒绝域为 。 1 =  2 =  =  p = 0    p , , , 1 2  y ˆ i = b0 + b1 xi1 ++ bp xi p，i = 1,2,  ,n E R n i i n i i i n i ST =  yi − y =  y − y + y − y = S + S = = =1 2 1 2 1 2 ( ) ( ˆ ) ( ˆ ) =  − i E i i S y y 2 ( ˆ ) f E = n − p −1 = − 2 S (y ˆ y) R i f R = p ~ ( , ) ( , 1) / / = F f f = F p n − p − S f S f F R E E E R R  ( , 1) F  F1− p n − p −