
三、误差的表示方法 (一)误差 1.绝对误差E E=X-XT X>X,E>0,表示测量结果偏高,反之。 【例题1】 2 相对误差E E F'= ×100% XT X=X红x100% X 【例题2】计算例题1的相对误差 2003-3 第二章误差与分析数据的处理 11
2003-3 三、误差的表示方法 : 1. E E = Xi − XT Xi XT , E 0 , 表示测量结果偏高,反之。 【例题1】 2. E’ E E X X X X T i T T ' % % = = − 100 100 【例题2】计算例题1的相对误差

说明 ①E具有狭意性,应用范围有限;E具有广义性,应 用范围广: ②绝对误差不能完全表示测量的准确度; ③不能以表面形式(%)的有无来判断是E还是E。 2003-3 第二章误差与分析数据的处理 12
2003-3 ①E具有狭意性,应用范围有限;E'具有广义性,应 用范围广; ②绝对误差不能完全表示测量的准确度; ③不能以表面形式(%)的有无来判断是E还是E
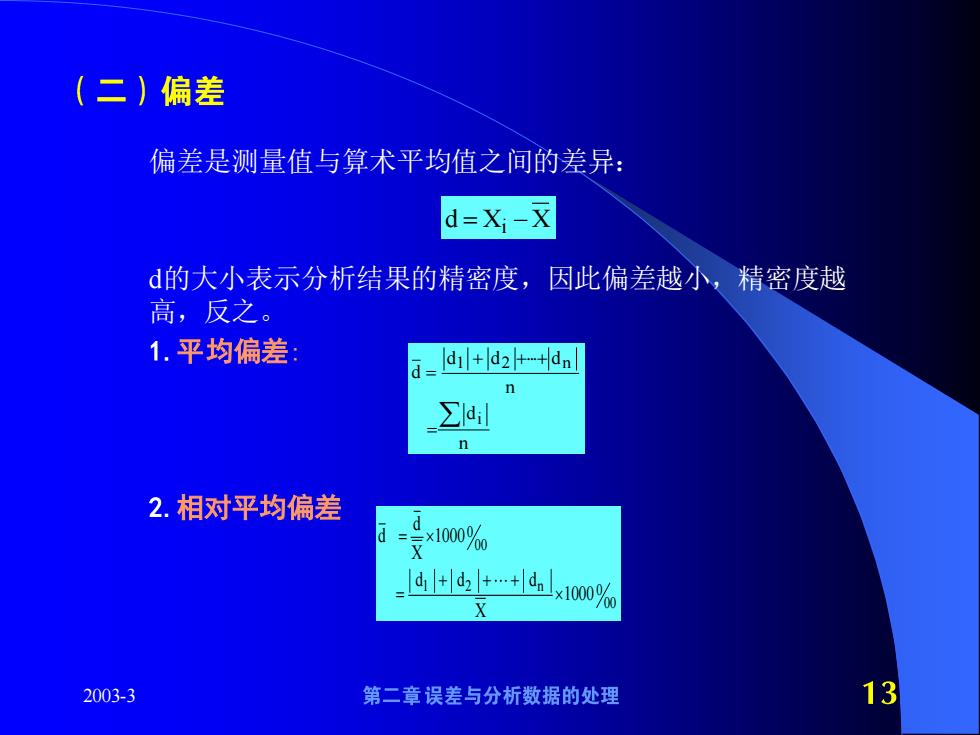
(二)偏差 偏差是测量值与算术平均值之间的差异: d=Xj-X d的大小表示分析结果的精密度,因此偏差越小,精密度越 高,反之。 1.平均偏差: d1 +d2++dn ∑ 2.相对平均偏差 ×1000% dt+-+18x10o%0 X 2003-3 第二章误差与分析数据的处理 13
2003-3 偏差是测量值与算术平均值之间的差异: d的大小表示分析结果的精密度,因此偏差越小,精密度越 高,反之。 1.平均偏差: 2.相对平均偏差 d X X = −i n d n d d d d i 1 2 n = + ++ = 0 00 1 2 n 0 00 d d 1000 X d d d 1000 X = + + + =

3.标准偏差 ∑x-X2 n-1 式中n-1称为自由度,用f表示。通常是指独立变数的个数。 3.相对标准偏差 ×1000%0 说明:标准偏差是将偏差先平方起来再总和,避免了相加时正、负抵消, 使大偏差更加显著地反映出来,能更好地说明数据的分散性,如 第一批数据:+0.3,+0.2,-0.4,-0.2,+0.1,+0.4,0.0,-0.3,+0.2,-0.3 第二批数据:0.0,+0.1,-0.7*,+0.2,-0.1,-0.2,+0.5*,-0.2,+0.3,+0.1; 2003-3 第二章误差与分析数据的处理
2003-3 3. 标准偏差 式中 n-1 称为自由度,用f 表示。 通常是指独立变数的个数。 2 (X X) S n 1 − = − 3. 相对标准偏差 c v s X . = 1000 0 00 标准偏差是将偏差先平方起来再总和,避免了相加时正、负抵消, 使大偏差更加显著地反映出来,能更好地说明数据的分散性,如 第一批数据: +0.3, +0.2, -0.4, -0.2, +0.1, +0.4, 0.0, -0.3, +0.2, -0.3; 第二批数据: 0.0, +0.1, -0.7*, +0.2, -0.1, -0.2, +0.5*, -0.2, +0.3, +0.1;
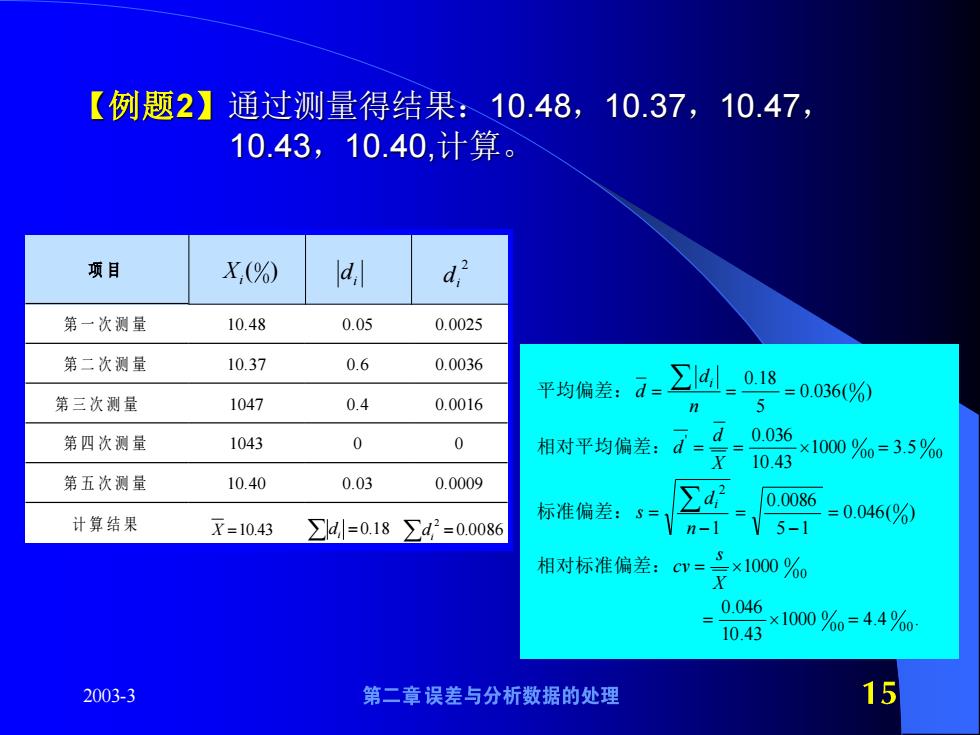
【例题2】通过测量得结果:10.48,10.37,10.47, 10.43,10.40,计算。 项目 X(%) la, d 第一次测量 10.48 0.05 0.0025 第二次测量 10.37 0.6 0.0036 第三次测量 =0.036(%0 1047 0.4 0.0016 平均偏差:-∑1叫018 n 5 第四次测量 1043 0 0 相对平均偏差:d==0036 10.43 ×1000%0=35%0 第五次测量 10.40 0.03 0.0009 0.0086 计算结果 标准偏差:$三 X=10.43 ∑=0.18∑d2=0.0086 n-1 V5-1 =0.046(%0 相对标准偏差:w=三×100%0 0.046 10.43 ×1000%0=4.4%0 2003-3 第二章误差与分析数据的处理 15
2003-3 【例题2】通过测量得结果:10.48,10.37,10.47, 10.43,10.40,计算。 1000 4.4 . 10.43 0.046 1000 0.046( ) 5 1 0.0086 1 1000 3.5 10.43 0.036 0.036( ) 5 0.18 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 ' 0 0 = = = = − = − = = = = = = = X s c v n d s X d d n d d i i 相对标准偏差: 标准偏差: 相对平均偏差: 平均偏差: 项 目 第 一 次 测 量 10.48 0.05 0.0025 第 二 次 测 量 10.37 0.6 0.0036 第 三 次 测 量 1047 0.4 0.0016 第 四 次 测 量 1043 0 0 第 五 次 测 量 10.40 0.03 0.0009 计 算 结 果 ( )0 0 Xi i d 2 di X =10.43 di = 0.18 = 0.0086 2 di