
E.(=)-IE F.(=)-,Eme 媒质1中的反射波: E(=)=E.(=)+E.(=)=2,Em(:+h:) 月,(e)=A.(e)+i,(e)=8,E(ea-re4) 媒质1中的合成波: n E3(=)=E.(=)=rE H()-()m 媒质2中的透射波: 合成波的特点 E(=)=E() ,E(1+)e+(ein:-e-) =Em(1+)e:+j2rsin(B) 这种由行波和纯驻波合成的波称为行驻波(混合波) 合成波电场振幅仁>0) E()=E1+TeA:=E+r2+2r Cos(2B=) 当民=-n元,即=-n/2(=0,12,时,有 E(=)=Em+r 当B.=-n+)x/2,即=(2+4%=0,12,时,有 E(e以=E1- 92/472/45元/432/4元/41 合成波电 场垢短 7 合成波电 5/2 2 32/2 /2 6
6 媒质 1 中的反射波: 1 1 j r im im j r 1 ( ) e ( ) e z x z y E z e E E H z e = = − 媒质 1 中的合成波: 1 1 1 1 j j 1 i r im im j j 1 i r 1 ( ) ( ) ( ) (e e ) ( ) ( ) ( ) (e e ) z z x z z y E z E z E z e E E H z H z H z e − − = + = + = + = − 媒质 2 中的透射波: 2 2 j 2 t im j im 2 t 2 ( ) ( ) e ( ) ( ) e z x z y E z E z e E E H z H z e − − = = = = 合成波的特点 1 1 1 1 1 1 j j 1 im j j j im j im 1 ( ) (e e ) (1 )e (e e ) (1 )e j2 sin( ) z z x z z z x z x E z e E e E e E z − − − − = + = + + − = + + 这种由行波和纯驻波合成的波称为行驻波(混合波) 合成波电场振幅 ( 0) 1 j2 2 1 im im 1 ( ) 1 e 1 2 cos(2 ) z E z E E z = + = + + 当 1z = −n ,即 2 ( 0,1,2, ) z = −n1 n = 时,有 1 im max E z E ( ) 1 = + 当 1z = −(2n +1) 2 ,即 ( 2 1 4) ( 0,1,2, ) z = − n + 1 n = 时,有 1 im min E z E ( ) 1 = − 51 / 2 21 31 / 2 1 1 / 2 91 4 71 4 51 4 31 4 1 4 —— 合成波电 场振幅 —— 合成波电 场 z

9入/472/45入/432/4:元/4 、合成波电 一合成波电 52/2'2九3元/2 合成波电场振幅仁>0) E(=)=E1+rePA:=E1+2+2TCOS(2B=) 当A:=-n元,即=-n/2(n=0,12.时,有 (e以=El+ 当R.=-2n+0π/2,即=-(/2+4以n=01,2.时,有 (e以=E1-小 驻波系数(驻波比)S 驻波系数、定义为驻波的电场强度振幅的最大值与最小值之比,即 1+ s党明→n别 讨 当「=0时,S礼,为行波。 当「=士1时,S二0,是纯驻波。 当0<口<1时,1<S<0,为混合波。S越大,驻波分量越大,行波分量越小: 例6.12在自由空间,一均匀平面波垂直入射到半无限大的无耗介质平面上,已知自由空间中, 合成波的驻波比为3,介质内传输波的波长是自由空间波长的16,且分界面上为驻波电场的最 小点。求介质的相对磁导率和相对介电常数。 s-识-3→n-号 解:因为驻波比1一 =
7 合成波电场振幅 ( 0) 1 j2 2 1 im im 1 ( ) 1 e 1 2 cos(2 ) z E z E E z = + = + + 当 1z = −n ,即 2 ( 0,1,2, ) z = −n1 n = 时,有 1 im min E z E ( ) 1 = + 当 1z = −(2n +1) 2 ,即 ( 2 1 4) ( 0,1,2, ) z = − n + 1 n = 时,有 1 im max E z E ( ) 1 = − 驻波系数(驻波比) S 驻波系数 S 定义为驻波的电场强度振幅的最大值与最小值之比,即 max min 1 1 E S E + = = − 1 1 + − = S S 讨论 当 = 0 时, S =1 ,为行波。 当 = 1 时, S = ,是纯驻波。 当 0 1 时, 1 S ,为混合波。 S 越大,驻波分量越大,行波分量越小; 例 6.1.2 在自由空间,一均匀平面波垂直入射到半无限大的无耗介质平面上,已知自由空间中, 合成波的驻波比为 3,介质内传输波的波长是自由空间波长的 1/6,且分界面上为驻波电场的最 小点。求介质的相对磁导率和相对介电常数。 解:因为驻波比 1 3 1 S + = = − 1 2 = 51 / 2 21 31 / 2 1 1 / 2 91 4 71 4 51 4 31 4 1 4 —— 合成波电 场振幅 —— 合成波电 场 z 6 0 0 2 = = r r
由于界面上是鞋淡电场的最小点,故厂一弓 1 而反射系数 2+7 式中 4=2 ◇ 8,=18 又因为2区的波长 电磁能流密度 媒质1中沿z方向传播的平均功率密度 瓦-e[Ex]-e 入射波平均功率 1密度减去反射波 &[E×]-民r医 及[6×]-n- 4。,=0 媒质2中的平均功率密度 H.H 及[医]-er 1-r2=0+r1-r)=hx2 64,=36 由 172 Sly S2a 例6.13入射波电场兵=E,100c0s6x101-10xr/m,从空气<0)中正入射到=0的 平面边界面上。在2>0区域中,从,=1、8,=4。求区域>0的电场和磁场。 解:z>0区域的本征阻抗 _120m=60x0 2
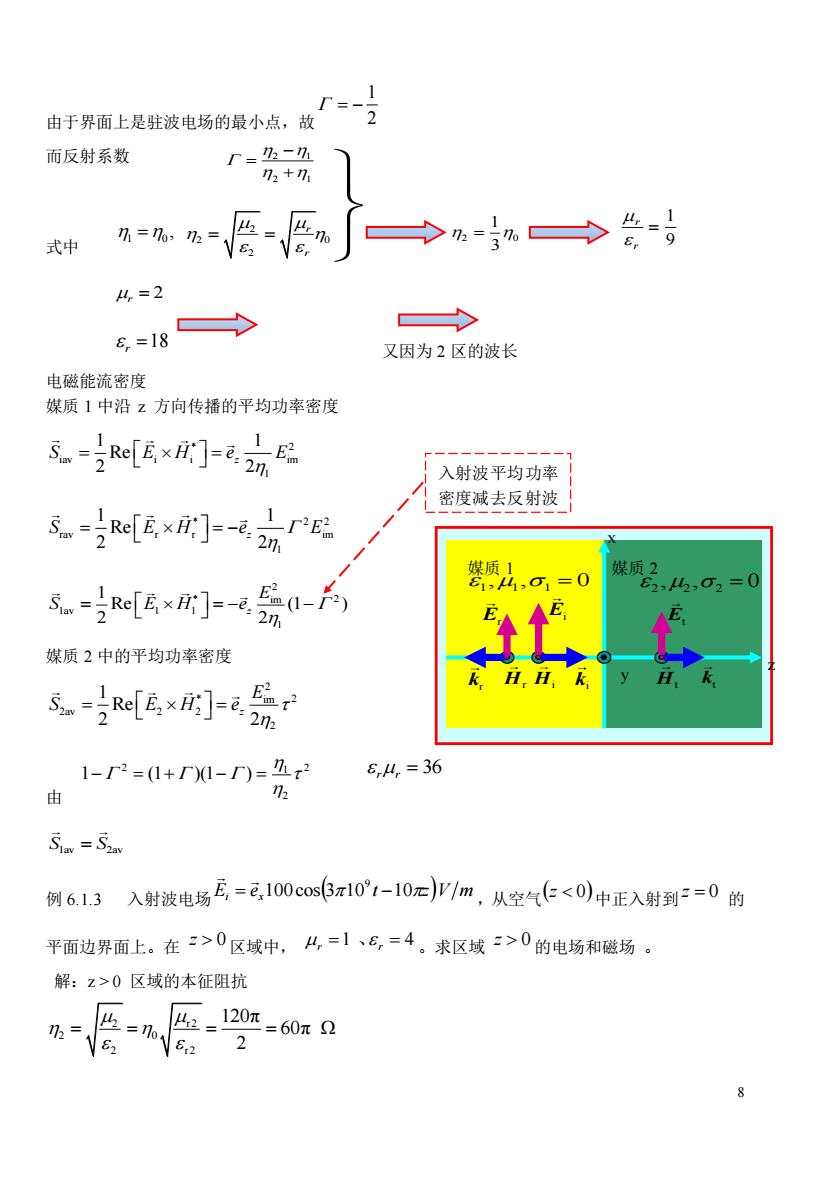
8 由于界面上是驻波电场的最小点,故 1 2 = − 而反射系数 式中 2 0 3 1 = 9 1 = r r r = 2 18 r = 又因为 2 区的波长 电磁能流密度 媒质 1 中沿 z 方向传播的平均功率密度 * 2 iav i i im 1 1 1 Re 2 2z S E H e E = = * 2 2 rav r r im 1 1 1 Re 2 2z S E H e E = = − 2 * 2 im 1av 1 1 1 1 Re (1 ) 2 2z E S E H e = = − − 媒质 2 中的平均功率密度 2 * 2 im 2av 2 2 2 1 Re 2 2z E S E H e = = 由 2 2 1 2 1 (1 )(1 ) − = + − = S S 1av 2av = 例 6.1.3 入射波电场 Ei ex100cos(310 t 10z)V m 9 = − ,从空气 (z 0) 中正入射到 z = 0 的 平面边界面上。在 z 0 区域中, r =1 、 r = 4 。求区域 z 0 的电场和磁场 。 解:z > 0 区域的本征阻抗 2 r2 2 0 2 r2 120π 60π Ω 2 = = = = 2 1 2 1 − = + 1 0 = , 2 2 0 2 r r = = rr = 36 入射波平均功率 密度减去反射波 平均功率密度 媒质 1 媒质 2 1 ,1 ,1 = 0 2 ,2 , 2 = 0 z x y Ei Hi ki Er kr Hr Et Ht kt

透射系数 t=2 2×60π %+%i120m+60元=0.667 相位常数 A=a=oG后-82=0m E=@,E2 cos(ot-B,=)=&,rE cos(@t-B,=) =e,0.667×10cos(3π×10°1-20me) =e,6.67cos(3π×10°1-20mc)Vm 月,=1e×E, c3-20) =e0.036cos(3π×10°1-20z)A/m 例614已知媒质1的1=4“m=lG=0:媒质2的S2=10、4:=43=0。角 须率0=5×I0d5的均匀平面波从媒质1垂直入射到分界面上,设入射波是沿x轴方向的 线极化波,在1=0、:=0时,入射波电场的振幅为2.4ym。求: )B和A:(2反射系数5和5:③1区的电场(,):2区的电场,(,). 解:(1) nalm 月=ag56-go-l034adm 4 9
9 透射系数 2 1 2 2 2 60π 0.667 120π 60π = = = + + 相位常数 故 9 2 2 2 0 0 r2 8 3π 10 2 20π rad/m 3 10 = = = = 2 2m 2 im 2 9 9 cos( ) cos( ) 0.667 10cos(3π 10 20π ) 6.67cos(3π 10 20π ) V/m x x x x E e E t z e E t z e t z e t z = − = − = − = − 2 2 2 9 9 1 6.67 cos(3π 10 20π ) 60π 0.036cos(3π 10 20π ) A/m z y y H e E e t z e t z = = − = − 例 6.1.4 已知媒质 1 的 r1 = 4、r1 =1、1 = 0 ; 媒质 2 的 r 2 =10、r 2 = 4、 2 = 0 。角 频率 rad s 8 = 510 的均匀平面波从媒质 1 垂直入射到分界面上,设入射波是沿 x 轴方向的 线极化波,在 t = 0、z = 0 时,入射波电场的振幅为 2.4V m 。求: (1) 1 和 2 ; (2) 反射系数 1 和 2 ;(3) 1 区的电场 E (z,t) 1 ;(4) 2 区的电场 E (z,t) 2 。 解:(1) 8 1 1 1 0 0 r1 r1 8 5 10 2 3.33 rad/m 3 10 = = = = 8 2 0 0 r2 r2 8 5 10 10 4 10.54 rad/m 3 10 = = = (2) 1 r1 1 0 0 1 r1 1 60π Ω 2 = = = = 2 r2 2 0 0 2 r2 4 75.9π Ω 10 = = =

=2=h=759-60=0.117 72+7160+75.9 (3)1区的电场 E(=)=E(z)+E(z)=eE (e+ei) =E[(1+)e+j2rsin(B=)] =E,2.41.117e33:+j0.234sin(3.33z 或E(e)=E(e)+E,(e)=e,2.4e83:+E,0.281e E(=,1)=ReE(=)e =e2.4c0s(5×103t-3.33z)+e.0.281cos(5×10t+3.33z) x=22≈1.12 (4) 71+72 故 E(=)=e Eme it=e,tEmeth =,1.12×2.4e-054:=,2.68e-i054 E2(z,t)=e2.68cos(5×10t-10.54z) 6.2均匀平面波对多层介质分界平面的垂直入射 本节内容 6.2.1多层介质中的场量关系与等效波阻抗 6.2.2四分之一波长匹配层 6.2.3半波长介质窗 6.2.1多层介质中的场量关系与等效波阻抗 电磁波在多层介质中的传播具有普遍的实际意义。 以三种介质形成的多层媒质为例,说明平面波在多层媒质中的传播过程及其求解方法。 如图所示,当平面波自媒质①向分界面垂直入射时,在媒质①和②之间的分界面上发生反射 和透射。当透射波到达媒质②和③的分界面时,又发生反射与透射,而且此分界面上的反射波回 到媒质①和②的分界面上时再次发生反射与诱射。 由此可见,在两个分界面上发生多次反射与透射现象。 媒质①和②中存在两种平面波,其一是向正z 方向传播的波,另一是向负z方向传播的波, 在媒质③中仅存在向正z方向传播的波。因此, 10
10 0.117 60 75.9 75.9 60 2 1 2 1 = + − = + − = (3) 1 区的电场 1 1 1 j j 1 i r im j im 1 j3.33 ( ) ( ) ( ) (e e ) [(1 )e j2 sin( )] 2.4[1.117e j0.234sin(3.33 )] z z x z x z x E z E z E z e E e E z e z − − − = + = + = + + = + 或 j3.33 j3.33 1 i r ( ) ( ) ( ) 2.4e 0.281e z z E z E z E z e e x x − = + = + j 1 1 8 8 ( , ) Re ( )e 2.4cos(5 10 3.33 ) 0.281cos(5 10 3.33 ) t x x E z t E z e t z e t z = = − + + (4) 1.12 2 1 2 2 + = 故 2 2 j j 2 tm im ( ) e e z z E z e E e E x x − − = = j10.54 j10.54 1.12 2.4e 2.68e z z x x e e − − = = 8 2 ( , ) 2.68cos(5 10 10.54 ) E z t e t z = − x 6.2 均匀平面波对多层介质分界平面的垂直入射 本节内容 6.2.1 多层介质中的场量关系与等效波阻抗 6.2.2 四分之一波长匹配层 6.2.3 半波长介质窗 6.2.1 多层介质中的场量关系与等效波阻抗 电磁波在多层介质中的传播具有普遍的实际意义。 以三种介质形成的多层媒质为例,说明平面波在多层媒质中的传播过程及其求解方法。 如图所示,当平面波自媒质①向分界面垂直入射时,在媒质①和②之间的分界面上发生反射 和透射。当透射波到达媒质②和③的分界面时,又发生反射与透射,而且此分界面上的反射波回 到媒质①和②的分界面上时再次发生反射与透射。 由此可见,在两个分界面上发生多次反射与透射现象。 媒质①和②中存在两种平面波,其一是向正 z 方向传播的波,另一是向负 z 方向传播的波, 在媒质③中仅存在向正 z 方向传播的波。因此