
19世纪末,经典物理学(牛顿力学、热力学及经典统计、经典电磁 理论)取得的成就给人的印象极为深刻,所有已知的物理现象似乎都能在 一个普遍的物质微粒和辐射波动理论中给出解释。 如果遇到无法解释的情况,人们也有理由把失败归咎于出来这些问 题中的数学困难,而不会去归罪基本方程的形式。 但是在19世纪末、20世纪初,当物理学的研究扩展到高速微观领域 时,经典物理学遇到了一系列困难,为克服这些困难,在高速领域建立了 相对论,在微观领域建立了量子力学
19世纪末,经典物理学(牛顿力学、热力学及经典统计、经典电磁 理论)取得的成就给人的印象极为深刻,所有已知的物理现象似乎都能在 一个普遍的物质微粒和辐射波动理论中给出解释。 如果遇到无法解释的情况,人们也有理由把失败归咎于出来这些问 题中的数学困难,而不会去归罪基本方程的形式。 但是在19世纪末、20世纪初,当物理学的研究扩展到高速微观领域 时,经典物理学遇到了一系列困难,为克服这些困难,在高速领域建立了 相对论,在微观领域建立了量子力学

经典物理学的困难 经典力学在微观领域领域遇到的困难主要体现在三个方面: ●经典物理学关于能量连续变换的概念无法解释黑体辐射的能谱 。光(辐射)的波动理论无法解释象光电效应这类涉及光与物质相互作用 的问题 ●把电子当成经典粒子,经典物理学无法解释原子的稳定性、氢原子光谱
经典力学在微观领域领域遇到的困难主要体现在三个方面: ⚫ 经典物理学关于能量连续变换的概念无法解释黑体辐射的能谱 ⚫ 光(辐射)的波动理论无法解释象光电效应这类涉及光与物质相互作用 的问题 ⚫ 把电子当成经典粒子,经典物理学无法解释原子的稳定性、氢原子光谱 经典物理学的困难

一、黑体辐射(Black-body radiation) 在绝对温度零度以上,任何物体都向外辐 射电磁波(能量),也吸收投射到它上面 反射某些波长的辐射能 的电磁波(能量)。Ki rchhoff热辐射定 不透明体 (随物而异) 处 律—一在热平衡情况下,物体的谱发射率 于 T)吸收某些波长的辐射能 某 (随物而异) e(v,T)与谱吸收率a(v,T)之比只与温度T 和频率V有关,而与物体本身性质无关, 发射各种波长的热辐射能 (故亦随物而异) 即 e(v,T) a(v,T) f(v,T) 吸收的辐射能量 0≤a(y,T)= 投射的辐射能量≤1
在绝对温度零度以上,任何物体都向外辐 射电磁波(能量),也吸收投射到它上面 的电磁波(能量)。 Kirchhoff热辐射定 律——在热平衡情况下,物体的谱发射率 𝑒 𝜈, 𝑇 与谱吸收率𝑎 𝜈, 𝑇 之比只与温度𝑇 和频率𝜈有关,而与物体本身性质无关, 即 𝑒 𝜈, 𝑇 𝑎 𝜈, 𝑇 = 𝑓 𝜈, 𝑇 0 ≤ 𝑎 𝜈, 𝑇 = 吸收的辐射能量 投射的辐射能量 ≤ 1 一、黑体辐射(Black-body radiation)
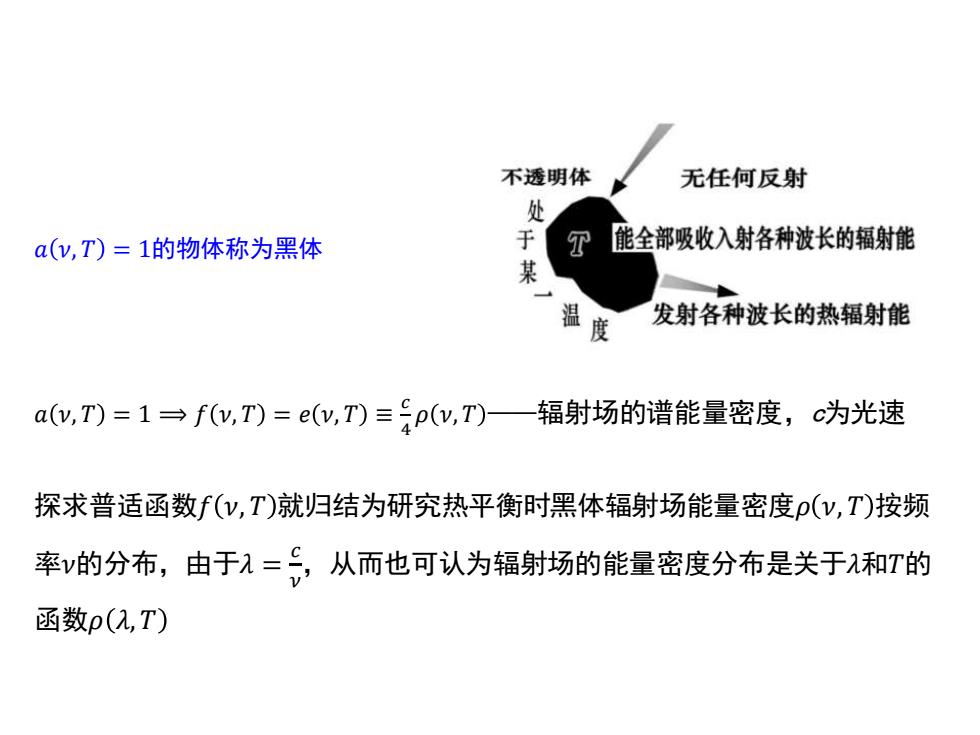
不透明体 无任何反射 处 a(y,T)=1的物体称为黑体 于 能全部吸收入射各种波长的辐射能 某 度 发射各种波长的热辐射能 a(w,T)=1→f(w,T)=e(,T)三p(y,T)一辐射场的谱能量密度,c为光速 探求普适函数f(y,T)就归结为研究热平衡时黑体辐射场能量密度p(y,T)按频 率v的分布,由于1=,从而也可认为辐射场的能量密度分布是关于和T的 函数p(2,T)
探求普适函数𝑓 𝜈, 𝑇 就归结为研究热平衡时黑体辐射场能量密度𝜌 𝜈, 𝑇 按频 率𝜈的分布,由于𝜆 = 𝑐 𝜈 ,从而也可认为辐射场的能量密度分布是关于𝜆和𝑇的 函数𝜌 𝜆, 𝑇 𝑎 𝜈, 𝑇 = 1的物体称为黑体 𝑎 𝜈, 𝑇 = 1 ⟹ 𝑓 𝜈, 𝑇 = 𝑒 𝜈, 𝑇 ≡ 𝑐 4 𝜌 𝜈, 𝑇 ——辐射场的谱能量密度,c为光速
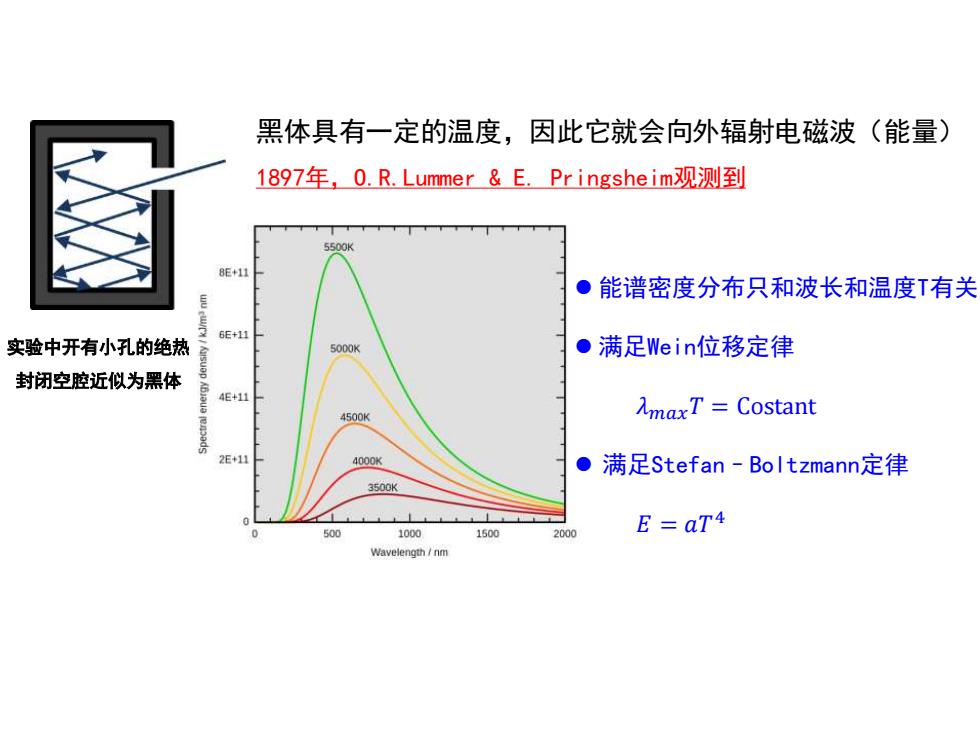
黑体具有一定的温度,因此它就会向外辐射电磁波(能量) 1897年,0.R.Lummer&E.Pringsheim/观测到 8E+11 ●能谱密度分布只和波长和温度T有关 6E+11 实验中开有小孔的绝热 5000K ●满足Wein位移定律 封闭空腔近似为黑体 4E+11 4500K AmaxT=Costant 2E+11 4000K ●满足Stefan-Boltzmann定律 3500K 500 1000 1500 2000 E=aT4 Wavelength/nm
实验中开有小孔的绝热 封闭空腔近似为黑体 黑体具有一定的温度,因此它就会向外辐射电磁波(能量) 1897年,O.R.Lummer & E. Pringsheim观测到 ⚫ 能谱密度分布只和波长和温度T有关 ⚫ 满足Wein位移定律 𝜆𝑚𝑎𝑥𝑇 = Costant ⚫ 满足Stefan–Boltzmann定律 𝐸 = 𝑎𝑇 4