
实验人员衣服着火时,切勿乱跑,应赶快脱下衣服,用石棉布覆盖着火处,或者就地卧 倒滚打,也可起到灭火的作用。火势较大,应立即报火警。 四、误差与有效数字 (一)误差的基本概念 1、测量中的误差。 任何测量过程都包含着误差。按其性质的不同误差可分为三类,即系统误差、偶然 误差和过失误差。 (1)系统误差 也称可测误差,是由某些比较确定的原因引起的,它对测量结果的影响比较固定, 其大小有一定规律性,在重复测量时,会重复出现。产生系统误差的主要原因有:实验 方法不完善;所用的仪器准确度差:药品不纯以及操作不当等。系统误差可以用改善方 法、校正仪器、提纯药品、做空白试验、对照试验的方法来减少。有时也可以在找出误 差原因后,算出误差的大小而加以修正 (2)偶然误差 也称随机误差或难测误差,由某些难以预料的偶然因素引起,它对实验结果的影响 不固定。由于偶然误差的原因难以确定,似乎无规律性可寻,但如果多次测量,可以发 现偶然误差遵从正态分布,即大小相近的正负误差出现机会相等,小误差出现的概率大, 大误差出现的概率很小。因此,通过多次测量取平均值的方法可以减少偶然误差对测量 结果的影响。 (3)过失误差 这是一种与事实明显不符的误差,由分析过程中的器皿不洁、加错试剂、错用样品、 试样损失、仪器出现异常未被发现、读错数据、计算错误等不应有的错误造成。过失误 差无规律可循,但只要加强责任心,工作认真细致即可避免。 2、准确度与误差 准确度系指在特定的条件下获得的分析结果与真实值之间的符合程度。准确度由分 析的偶然误差和系统误差决定,它能反映分析结果的可靠性。要想提高分析结果的准确 度,不仅需要改善分析的精密度,同时要消除系统误差。 准确度用绝对误差或相对误差表示。绝对误差是指实验测得的数值与真实值之间的 差值:相对误差指绝对误差与真实值的百分比。即 绝对误差=测定值一真实值 相对误差=绝对误差×100。 真实值
4 实验人员衣服着火时,切勿乱跑,应赶快脱下衣服,用石棉布覆盖着火处,或者就地卧 倒滚打,也可起到灭火的作用。火势较大,应立即报火警。 四、误差与有效数字 (一) 误差的基本概念 1、测量中的误差。 任何测量过程都包含着误差。按其性质的不同误差可分为三类,即系统误差、偶然 误差和过失误差。 (1) 系统误差 也称可测误差,是由某些比较确定的原因引起的,它对测量结果的影响比较固定, 其大小有一定规律性,在重复测量时,会重复出现。产生系统误差的主要原因有:实验 方法不完善;所用的仪器准确度差;药品不纯以及操作不当等。系统误差可以用改善方 法、校正仪器、提纯药品、做空白试验、对照试验的方法来减少。有时也可以在找出误 差原因后,算出误差的大小而加以修正。 (2)偶然误差 也称随机误差或难测误差,由某些难以预料的偶然因素引起,它对实验结果的影响 不固定。由于偶然误差的原因难以确定,似乎无规律性可寻,但如果多次测量,可以发 现偶然误差遵从正态分布,即大小相近的正负误差出现机会相等,小误差出现的概率大, 大误差出现的概率很小。因此,通过多次测量取平均值的方法可以减少偶然误差对测量 结果的影响。 (3)过失误差 这是一种与事实明显不符的误差,由分析过程中的器皿不洁、加错试剂、错用样品、 试样损失、仪器出现异常未被发现、读错数据、计算错误等不应有的错误造成。过失误 差无规律可循,但只要加强责任心,工作认真细致即可避免。 2、准确度与误差 准确度系指在特定的条件下获得的分析结果与真实值之间的符合程度。准确度由分 析的偶然误差和系统误差决定,它能反映分析结果的可靠性。要想提高分析结果的准确 度,不仅需要改善分析的精密度,同时要消除系统误差。 准确度用绝对误差或相对误差表示。绝对误差是指实验测得的数值与真实值之间的 差值;相对误差指绝对误差与真实值的百分比。即 绝对误差=测定值-真实值 = 100% 真实值 绝对误差 相对误差

绝对误差与被测量的大小无关,而相对误差却与被测量的大小有关。一般来说,若 被测的量越大,相对误差越小。一般用相对误差来反映测定值与真实值之间的偏离程度 比用绝对误差更为合理。 3、精密度与偏差 精密度系指在一定条件下,重复分析同一样品所得测定值的一致程度,即测量结果 的再现性,由分析的偶然误差决定。 通常被测量的真实值很难准确知道,因此,一般只能用多次重复测量结果的平均值 代替真实值。这时单次测量结果与平均值之间的偏离就称为偏差。偏差与误差一样,也 有相对偏差与绝对偏差。 绝对偏差=单次测定值一平均值 相对偏差=绝对偏差 平均值 100% a-水-,Rd=x100%a为平均偏差,Ra为相对平均偏差) 从相对偏差的大小可以反映出测量结果再现性的好坏,即测量的精密度。相对偏差 小,则可视为再现性好,即精密度高。在一般的化学实验中,一般可以用平均偏差或相 对平均偏差表示。 4、提高测量结果准确度的方法 为了提高测量结果的准确度。应尽量减小系统误差、偶然误差和过失误差。认真仔 细地进行多次测量,取其平均值作为测量结果,这样可以减少系统误差。减少系统误差 的方法一般有:校正测量仪器与测量方法、空白试验与对照试验。 (二)有效数字 1、有效数字位数的确定 分析测试中,在记录测定数据时,测定值值所表示的准确程度应与测试时所用的测 量仪器及测试方法的精度相一致。通常测定时,一般可估计到测量仪器最小刻度的十分 位,在记录测定数据时,只应保留一位不确定数字,其余数字都应是准确的,通常称此 时所记录的数字为有效数字。记录和报告的测定结果只应包含有效数字,对有效数字的 位数不能任意增删。 化学实验中常用仪器的精度与实测数据有效数字位数的关系列于表1中
5 绝对误差与被测量的大小无关,而相对误差却与被测量的大小有关。一般来说,若 被测的量越大,相对误差越小。一般用相对误差来反映测定值与真实值之间的偏离程度 比用绝对误差更为合理。 3、精密度与偏差 精密度系指在一定条件下,重复分析同一样品所得测定值的一致程度,即测量结果 的再现性,由分析的偶然误差决定。 通常被测量的真实值很难准确知道,因此,一般只能用多次重复测量结果的平均值 代替真实值。这时单次测量结果与平均值之间的偏离就称为偏差。偏差与误差一样,也 有相对偏差与绝对偏差。 绝对偏差=单次测定值—平均值 从相对偏差的大小可以反映出测量结果再现性的好坏,即测量的精密度。相对偏差 小,则可视为再现性好,即精密度高。在一般的化学实验中,一般可以用平均偏差或相 对平均偏差表示。 4、提高测量结果准确度的方法 为了提高测量结果的准确度。应尽量减小系统误差、偶然误差和过失误差。认真仔 细地进行多次测量,取其平均值作为测量结果,这样可以减少系统误差。减少系统误差 的方法一般有:校正测量仪器与测量方法、空白试验与对照试验。 (二)有效数字 1、有效数字位数的确定 分析测试中,在记录测定数据时,测定值值所表示的准确程度应与测试时所用的测 量仪器及测试方法的精度相一致。通常测定时,一般可估计到测量仪器最小刻度的十分 位,在记录测定数据时,只应保留一位不确定数字,其余数字都应是准确的,通常称此 时所记录的数字为有效数字。记录和报告的测定结果只应包含有效数字,对有效数字的 位数不能任意增删。 化学实验中常用仪器的精度与实测数据有效数字位数的关系列于表 I-1 中。 100% (d Rd ) x d , Rd n x x d i = 为平均偏差, 为相对平均偏差 − = = 100% 平均值 绝对偏差 相对偏差
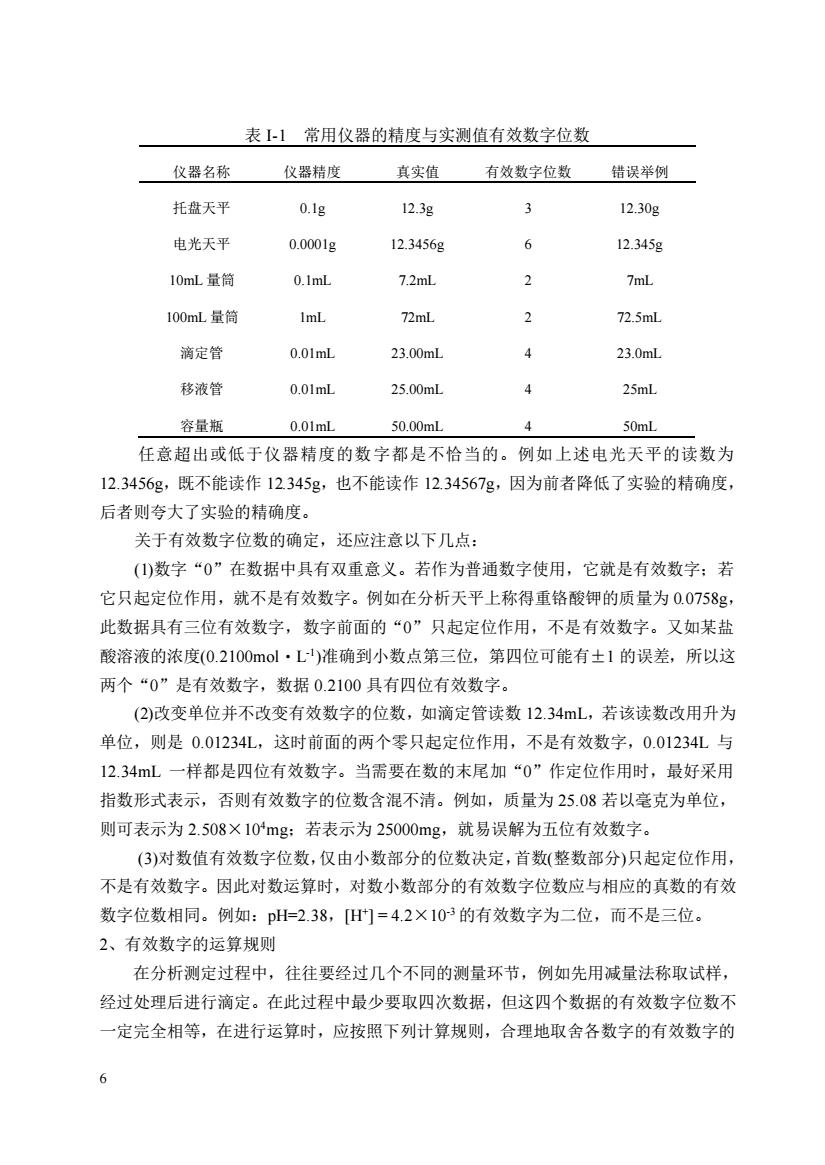
表【】常用仪器的精度与实测值有效数字位数 仪器名称 仪器精度 真实值 有效数字位数错误举例 托盘天平 0.1g 12.3g 2 12.30g 电光天平 0.0001g 12.3456g 6 12.345g 10mL量筒 0.1mL 7.2ml 2 7mL 100mL量简 72mL 72.5mL 滴定管 0.01m 23.00ml 23.0ml 移液管 0.01ml 25.00ml 4 25ml 究量瓶 0.01ml 50.00mL 4 50mL 任意超出或低于仪器精度的数字都是不恰当的。例如上述电光天平的读数为 12.3456g,既不能读作12345g,也不能读作12.34567g,因为前者降低了实验的精确度 后者则夸大了实验的精确度。 关于有效数字位数的确定,还应注意以下几点: ()数字“0”在数据中具有双重意义。若作为普通数字使用,它就是有效数字:若 它只起定位作用,就不是有效数字。例如在分析天平上称得重铬酸钾的质量为0.0758g, 此数据具有三位有效数字,数字前面的“0”只起定位作用,不是有效数字。又如某盐 酸溶液的浓度(0.2100mol·L)准确到小数点第三位,第四位可能有±1的误差,所以这 两个“0”是有效数字,数据0.2100具有四位有效数字。 (2)改变单位并不改变有效数字的位数,如滴定管读数12.34mL,若该读数改用升为 单位,则是0.01234L,这时前面的两个零只起定位作用,不是有效数字,0.01234L与 12.34mL一样都是四位有效数字。当需要在数的末尾加“0”作定位作用时,最好采用 指数形式表示,否则有效数字的位数含混不清。例如,质量为25.08若以毫克为单位, 则可表示为2.508×10mg:若表示为25000mg,就易误解为五位有效数字。 (3)对数值有效数字位数,仅由小数部分的位数决定,首数(整数部分)只起定位作用, 不是有效数字。因此对数运算时,对数小数部分的有效数字位数应与相应的真数的有效 数字位数相同。例如:pH=2.38,H=4.2×103的有效数字为二位,而不是三位。 2、有效数字的运算规则 在分析测定过程中,往往要经过几个不同的测量环节,例如先用减量法称取试样, 经过处理后进行滴定。在此过程中最少要取四次数据,但这四个数据的有效数字位数不 一定完全相等,在进行运算时,应按照下列计算规则,合理地取舍各数字的有效数字的
6 表 I-1 常用仪器的精度与实测值有效数字位数 仪器名称 仪器精度 真实值 有效数字位数 错误举例 托盘天平 0.1g 12.3g 3 12.30g 电光天平 0.0001g 12.3456g 6 12.345g 10mL 量筒 0.1mL 7.2mL 2 7mL 100mL 量筒 1mL 72mL 2 72.5mL 滴定管 0.01mL 23.00mL 4 23.0mL 移液管 0.01mL 25.00mL 4 25mL 容量瓶 0.01mL 50.00mL 4 50mL 任意超出或低于仪器精度的数字都是不恰当的。例如上述电光天平的读数为 12.3456g,既不能读作 12.345g,也不能读作 12.34567g,因为前者降低了实验的精确度, 后者则夸大了实验的精确度。 关于有效数字位数的确定,还应注意以下几点: (1)数字“0”在数据中具有双重意义。若作为普通数字使用,它就是有效数字;若 它只起定位作用,就不是有效数字。例如在分析天平上称得重铬酸钾的质量为 0.0758g, 此数据具有三位有效数字,数字前面的“0”只起定位作用,不是有效数字。又如某盐 酸溶液的浓度(0.2100mol•L -1 )准确到小数点第三位,第四位可能有±1 的误差,所以这 两个“0”是有效数字,数据 0.2100 具有四位有效数字。 (2)改变单位并不改变有效数字的位数,如滴定管读数 12.34mL,若该读数改用升为 单位,则是 0.01234L,这时前面的两个零只起定位作用,不是有效数字,0.01234L 与 12.34mL 一样都是四位有效数字。当需要在数的末尾加“0”作定位作用时,最好采用 指数形式表示,否则有效数字的位数含混不清。例如,质量为 25.08 若以毫克为单位, 则可表示为 2.508×104mg;若表示为 25000mg,就易误解为五位有效数字。 (3)对数值有效数字位数,仅由小数部分的位数决定,首数(整数部分)只起定位作用, 不是有效数字。因此对数运算时,对数小数部分的有效数字位数应与相应的真数的有效 数字位数相同。例如:pH=2.38,[H+ ] = 4.2×10-3 的有效数字为二位,而不是三位。 2、有效数字的运算规则 在分析测定过程中,往往要经过几个不同的测量环节,例如先用减量法称取试样, 经过处理后进行滴定。在此过程中最少要取四次数据,但这四个数据的有效数字位数不 一定完全相等,在进行运算时,应按照下列计算规则,合理地取舍各数字的有效数字的

位数,确保运算结果的正确。 (1)记录数据时,只保留一位有效数字。当拟舍弃的数字大于等于6时进位,而当尾 数怡为5时,则看保留的末位数是奇数还是偶数,是奇数时就将5进位,是偶数时,则 将5舍弃。总之,使保留下来的末位数是偶数,即“四舍六入五留双”。根据此原则, 如将4.175和4.165处理成三位数,则分别为4.18和4.16。 (2)进行数值加减时,最后结果所保留小数点后的位数应与参与运算的各数中小数点 后位数最少者相同。例如1.2379+12.46=13.6979应取13.70。 1.2379 +12.46 13.6979 (3)进行数值乘除时,最后结果的有效数字应以参与运算的各数中有效数字位数最 少者为准,而与小数点的位数无关。例如1.23×0.012-0.01476应取0.015。进行数值乘 方和开方时,保留原来的有效数字位数。 (4)在对数计算中,所取对数的小数点后的位数,应与真数的有效数字位数相同。 (⑤)测定平均值的精度应优于个别测定值,在计算不少于四个测定值的平均值时,平 均值的有效数字的位数可以比单次测定值的有效数字增加一位。 (6在所有计算式中,常数以及乘除因子的有效数字的位数可认为是足够的,应根据 需要确定有效数字的位数。 (7)表示分析方法的精密度和准确度时,大多数取12位有效数字
7 位数,确保运算结果的正确。 (1)记录数据时,只保留一位有效数字。当拟舍弃的数字大于等于 6 时进位,而当尾 数恰为 5 时,则看保留的末位数是奇数还是偶数,是奇数时就将 5 进位,是偶数时,则 将 5 舍弃。总之,使保留下来的末位数是偶数,即“四舍六入五留双”。根据此原则, 如将 4.175 和 4.165 处理成三位数,则分别为 4.18 和 4.16。 (2)进行数值加减时,最后结果所保留小数点后的位数应与参与运算的各数中小数点 后位数最少者相同。例如 1.2379+12.46=13.6979 应取 13.70。 1.2379 +12.46 13.6979 (3)进行数值乘除时,最后结果的有效数字应以参与运算的各数中有效数字位数最 少者为准,而与小数点的位数无关。例如 1.23×0.012=0.01476 应取 0.015。进行数值乘 方和开方时,保留原来的有效数字位数。 (4)在对数计算中,所取对数的小数点后的位数,应与真数的有效数字位数相同。 (5)测定平均值的精度应优于个别测定值,在计算不少于四个测定值的平均值时,平 均值的有效数字的位数可以比单次测定值的有效数字增加一位。 (6)在所有计算式中,常数以及乘除因子的有效数字的位数可认为是足够的,应根据 需要确定有效数字的位数。 (7)表示分析方法的精密度和准确度时,大多数取 1~2 位有效数字

Ⅱ化学实验的常用仪器介绍 一、天平 在定量分析中,精确称取基准物质标定标淮溶液,或称取分析样品时,都必须使用分析 天平。分析天平的构造精巧,灵敏度高,必须正确操作。称量正确与否,将直接影响实验结 果的准确性。下面介绍两种常用的分析天平。 (一)电光天平 电光天平的构造如图Ⅱ1所示。 电光天平是根据杠杆原理设计的,电光天平应放在水平及坚固的水泥台上,要避免靠近 热源或阳光照射。为了防止潮湿、灰尘浸 入和空气流冲击,分析天平装于玻璃匣内, 并在匣内放硅胶或其他干燥剂。天平匣下 面有三个足,旋动前面二足,根据水平仪 调整天平,使其处于水平位置。 电光天平可准确称量至万分之一克 (0.0001)克。最高载重量一般为200克。它 的中央为天平柱,柱的顶端有一块由玛瑙 制成磨光的平板。在天平梁的中央,嵌有 棱角向下的三棱体(支点。此三棱体在 图Ⅱ1电光分析天平示意图 称量工作状态时才放在平板上。天平梁两 1横梁2.天平螺丝3.蹬型架4.指针5.支点刀 端的三棱体则棱角朝上,各悬一个蹬形架, 6.框里7.环码8.指数盘9.天平柱 天平盘即挂于蹬形架上。当关上升降枢纽 10.托叶(卿梁托)11.阻尼筒12.投影屏13.称盘 时,天平梁及天平盘就被托起,三棱体与 14.盘托15.螺旋脚6.脚垫17.升降枢组 平板脱离,整个天平就被架起。当顺时针 方向启动升降枢纽时,天平梁就会摆动或倾斜。天平的灵敏度,主要决定于三棱体的尖锐程 度。为了保护天平,减少棱角磨损,只有在看指针摆动时才启动升降枢纽,其余所有时间都 应把升降枢纽关上,使天平架起。 为了便于观察天平盘中哪一边较重,天平 梁向哪一边倾斜,在天平梁中间装有指针,若 右边较重,天平梁向右倾斜,指针则向左,指 10 针恒指向轻的一侧。天平梁两端装有二个带螺 旋的小轴,来回转动螺丝,可消除二臂不等重 的误差,调节天平的零点。较小的零点调节, 可由底座下部微动调节杆来调节。 图Ⅱ-2旋转器上的指数盘 8
8 II 化学实验的常用仪器介绍 一、天平 在定量分析中,精确称取基准物质标定标淮溶液,或称取分析样品时,都必须使用分析 天平。分析天平的构造精巧,灵敏度高,必须正确操作。称量正确与否,将直接影响实验结 果的准确性。下面介绍两种常用的分析天平。 (一)电光天平 电光天平的构造如图Ⅱ-1 所示。 电光天平是根据杠杆原理设计的,电光天平应放在水平及坚固的水泥台上,要避免靠近 热源或阳光照射。为了防止潮湿、灰尘浸 入和空气流冲击,分析天平装于玻璃匣内, 并在匣内放硅胶或其他干燥剂。天平匣下 面有三个足,旋动前面二足,根据水平仪 调整天平,使其处于水平位置。 电光天平可准确称量至万分之一克 (0.0001)克。最高载重量一般为 200 克。它 的中央为天平柱,柱的顶端有一块由玛瑙 制成磨光的平板。在天平梁的中央,嵌有 棱角向下的三棱体(支点刀)。此三棱体在 称量工作状态时才放在平板上。天平梁两 端的三棱体则棱角朝上,各悬一个蹬形架, 天平盘即挂于蹬形架上。当关上升降枢纽 时,天平梁及天平盘就被托起,三棱体与 平板脱离,整个天平就被架起。当顺时针 方向启动升降枢纽时,天平梁就会摆动或倾斜。天平的灵敏度,主要决定于三棱体的尖锐程 度。为了保护天平,减少棱角磨损,只有在看指针摆动时才启动升降枢纽,其余所有时间都 应把升降枢纽关上,使天平架起。 为了便于观察天平盘中哪一边较重,天平 梁向哪一边倾斜,在天平梁中间装有指针,若 右边较重,天平梁向右倾斜,指针则向左,指 针恒指向轻的一侧。天平梁两端装有二个带螺 旋的小轴,来回转动螺丝,可消除二臂不等重 的误差,调节天平的零点。较小的零点调节, 可由底座下部微动调节杆来调节。 图Ⅱ-1 电光分析天平示意图 1. 横梁 2. 天平螺丝 3. 蹬型架 4. 指针 5. 支点刀 6. 框罩 7. 环码 8. 指数盘 9. 天平柱 10. 托叶(即梁托) 11. 阻尼筒 12. 投影屏 13. 称盘 14. 盘托 15. 螺旋脚 6. 脚垫 17. 升降枢纽 图Ⅱ-2 旋转器上的指数盘