12毫尔气体常数R) 原则上,可以对一定量的气体直接测定P,V,T的数值,然后代入R=PVT一式 来计 但这个公式是理想气体的状态方程式,真实气体只有在压力很低时才接近于理想气体。 而当压力很低时,实验不易操作,不易得到精确数据,所以常采用外推法来求出PV)P→0 的数值。合理的外推是常常被采用的一种科学方法。 复气 一理想气体 8.40 T(333 820 都气 一氧化碳 氧气 1020304050 ()c02在不网温度下的实险结用 在同一温下不同气体的实验结果 如图所示,各种不同的气体不论温度如何,当压力趋于零时PVm)/T均趋于一个共同的极 限值R,R称为摩尔气体常数,可得到:R-83145J/mol.K 13拥想气估的状态图 对一定量的理想气体,例如是1mol,PVm=RT。式中三个变量P,V,T中,只有两个变 量是独立的。 如以P,V,T为空间坐标,当给定P,T值后,Vm的值就不是任意的,其值由状态 方程来决定。在P,V,T空间坐标中就可用一个点来表示该气体的状态。 若再给定另一个P,T值,则空间坐标中又有一个点代表该状态。于是众多状态点在空 间坐标中可构成一个曲面,所有符合于理想气体的气体都出现在这个曲面上, 日都满显加 下的关系: 叱- 这个曲面就是理想气体的状态图,也称为相图(P21图15) 1.理想气体pV=nRT R=8.314510JK1mol 妈温面
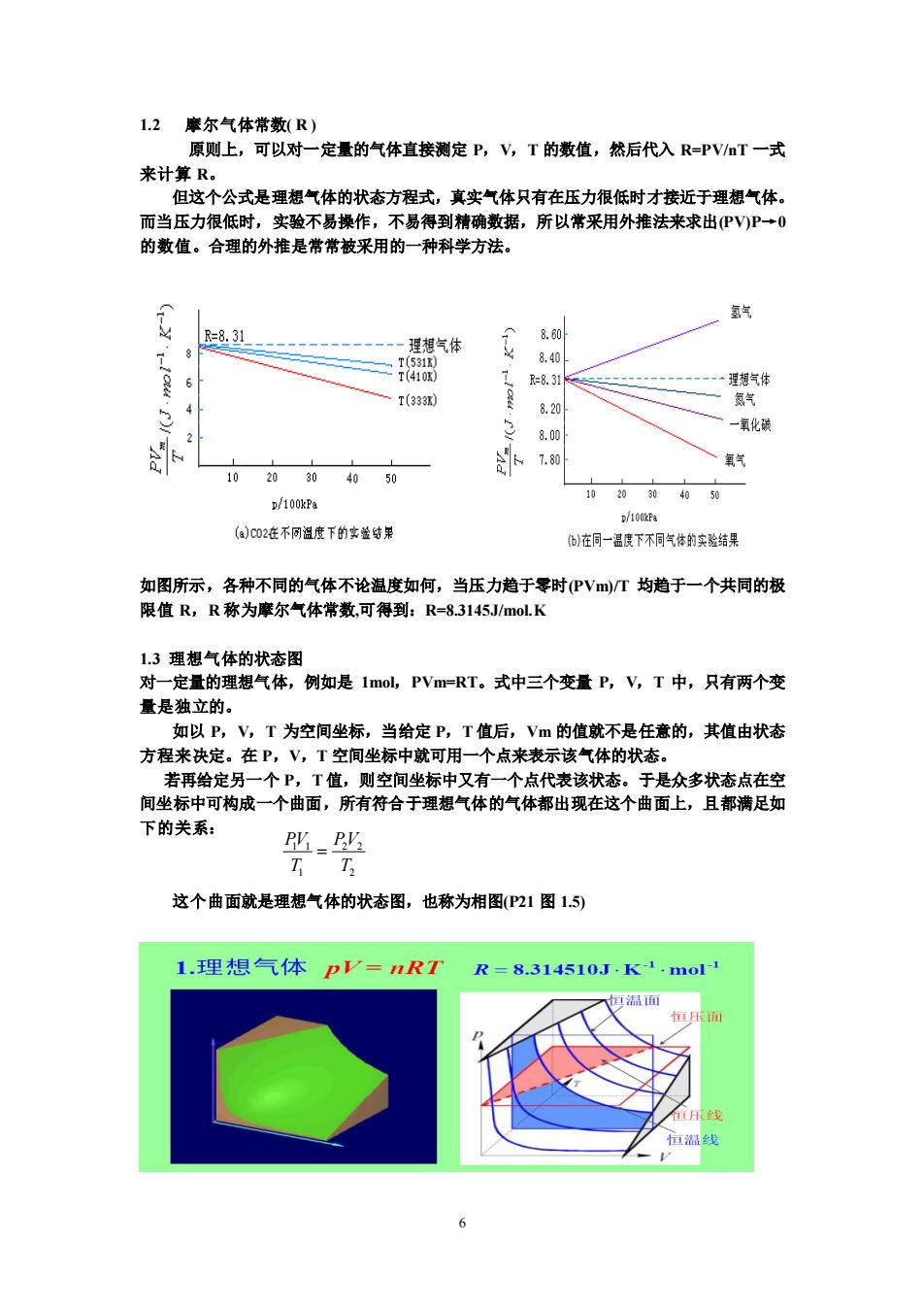
6 1.2 摩尔气体常数( R ) 原则上,可以对一定量的气体直接测定 P,V,T 的数值,然后代入 R=PV/nT 一式 来计算 R。 但这个公式是理想气体的状态方程式,真实气体只有在压力很低时才接近于理想气体。 而当压力很低时,实验不易操作,不易得到精确数据,所以常采用外推法来求出(PV)P→0 的数值。合理的外推是常常被采用的一种科学方法。 如图所示,各种不同的气体不论温度如何,当压力趋于零时(PVm)/T 均趋于一个共同的极 限值 R,R 称为摩尔气体常数,可得到:R=8.3145J/mol.K 1.3 理想气体的状态图 对一定量的理想气体,例如是 1mol,PVm=RT。式中三个变量 P,V,T 中,只有两个变 量是独立的。 如以 P,V,T 为空间坐标,当给定 P,T 值后,Vm 的值就不是任意的,其值由状态 方程来决定。在 P,V,T 空间坐标中就可用一个点来表示该气体的状态。 若再给定另一个 P,T 值,则空间坐标中又有一个点代表该状态。于是众多状态点在空 间坐标中可构成一个曲面,所有符合于理想气体的气体都出现在这个曲面上,且都满足如 下的关系: 这个曲面就是理想气体的状态图,也称为相图(P21 图 1.5) 1 1 2 2 1 2 PV PV T T =

1.4分子运动的速率分布 一、Maxwell速率分布定律 本节中所要讨论的问题是 速率落在 一定间隔Y+w内的分子有多少,落在哪一个间隔中的分子数最多: Maxwell于18s9年首先导出了分子速率的分布公式,后来Boltzmann用统计力学的方 法也得到相同的公式。 今设容器内有N个分子,速率在vv+dy范图内的分子有dv个,dNvN表示分子速率 在此范围中的分子占总分子数的分数。对于一个分 子来说,就是该分子的速率在一v+间 隔中的概率 (山)dNv显然与N和dv有关:总分子数越多,速率间隔越大,则dNv必越大。 (2)Nv也与速率v的大小有关,即虽然速率的间隔相同,而速率不同,则其分子数也不同。 dN.o Ndui或dN,=Nf(o)du 书P(1.20) fv:是一个与v及温度有关的函数,称为分布函数(distribution function) 一它的意义相当 于d小v=1时,即速率在V至v+1之间的分子在总分子中所占的分数。 Maxwell证得 将上式代入式1.20)则得Maxwell速率分布公式 P28图1.8是根据上式(书121)所画出的图形,图中纵坐标代表速率介于v至v+1之 间的分子占总分子数的分数,横坐标代表速率。每一条曲线下的面积恒等于1。 当温度升高时,速率的分布曲线变得较宽面平坦,最高点下移。这表明高温时,速率 的分布较宽广。 当温度较低时曲线陡峭,分子速率的分布为集中, 二、分子速率的三个统计平均值-最 然速率、数学平均速率与根均方速率 1、最概然速率:在Maxw速率分布曲线上有一最高点P28图(L8),该点表示具有这种速 率的分子所占的分数最大,这个最高点所对应的速率称之为最橛然速率(vm) 解得 ,2k7 m 或 2RT D.M 式中M为气体的摩尔质量。由此可见,最概然速率与质量的平方根成反比。在相同的温度 下,摩尔质量小的分子,其最概然速率大P2图(13) 2、分子的数学平均速率v:所有分子速率的数学平均值 8kT 3、根均方速率(): >
7 1.4 分子运动的速率分布 一、Maxwell 速率分布定律 本节中所要讨论的问题是: 速率落在一定间隔 v∼v+dv 内的分子有多少,落在哪一个间隔中的分子数最多? Maxwell 于 1859 年首先导出了分子速率的分布公式,后来 Boltzmann 用统计力学的方 法也得到相同的公式。 今设容器内有 N 个分子,速率在 v∼v+dv 范围内的分子有 dNv 个, dNv /N 表示分子速率 在此范围中的分子占总分子数的分数。对于一个分子来说,就是该分子的速率在 v∼v+dv 间 隔中的概率。 (1) dNv 显然与 N 和 dv 有关:总分子数越多,速率间隔越大,则 dNv 必越大。 (2)dNv 也与速率 v 的大小有关,即虽然速率的间隔相同,而速率不同,则其分子数也不同。 f(v):是一个与 v 及温度有关的函数,称为分布函数(distribution function)——它的意义相当 于 dv=1 时,即速率在 v 至 v+1 之间的分子在总分子中所占的分数 。 Maxwell 证得 将上式代入式(1.20)则得 Maxwell 速率分布公式 P28 图 1.8 是根据上式(书 1.21)所画出的图形,图中纵坐标 f(v) 代表速率介于 v 至 v+1 之 间的分子占总分子数的分数,横坐标代表速率。每一条曲线下的面积恒等于 1。 当温度升高时,速率的分布曲线变得较宽面平坦,最高点下移。这表明高温时,速率 的分布较宽广。 当温度较低时曲线陡峭,分子速率的分布为集中。 二、分子速率的三个统计平均值-最概然速率、数学平均速率与根均方速率 1、最概然速率:在 Maxwell 速率分布曲线上有一最高点 P28 图(1.8),该点表示具有这种速 率的分子所占的分数最大,这个最高点所对应的速率称之为最概然速率(vm) 解得 或 式中 M 为气体的摩尔质量。由此可见,最概然速率与质量的平方根成反比。在相同的温度 下,摩尔质量小的分子,其最概然速率大 P28 图(1.8) 。 2、分子的数学平均速率(va):所有分子速率的数学平均值。 3、根均方速率(u): dN Nd dN Nf d ( ) = 或 22 书P (1.20) 1.5 2 4 2 ( ) exp 2 2 m m f kT kT − = 1.5 2 4 2 exp 2 2 dN m m d N kT kT − = 2 b m k T m = 2 m RT M = 8 a kT m =