
Energy is force x distance dE=-Fdy dE=kydy Total Energy ∫dE=k∫ydy 0 0 1. B=2为2 Parabolic E vs.displacement curve of harmonic oscillator 0 Displacement y- (Fig16-3) CEM 333 page 6.6
Energy is force ´ distance dE = -Fdy dE = kydy Total Energy dE 0 E ò = k ydy o y ò E = 1 2 ky2 Parabolic E vs. displacement curve of harmonic oscillator (Fig 16-3) CEM 333 page 6.6

Classical vibrational frequency: 1k Vclassical= 2元Vm v independent of energy Two masses? 4= mm2 Velassical reduced mass 2πVu m1+m2 What about quantum mechanics? (1) E=v+2)2元Vu Vibrational quantum number(0,1,2.) EhVdrscl Ground vibrational state (v=0) 3 E1hVclassical First excited state(v=1) △E=hVclassical Calculated AE often agrees quite well with experiment Vealeulated (C=O)=1600 cm-1 Vexperiment(C=O)=1600-1800 cm-1 See example 16-1 (2)△V=±1 Vibrational Selection Rule Since levels equally spaced-should see one absorption frequency CEM 333 page 6.7
Classical vibrational frequency: nclassical = 1 2p k m n independent of energy Two masses? nclassical = 1 2p k m m = m1 ×m2 m1 + m2 reduced mass What about quantum mechanics? (1) E = n + 1 2 æ è ö ø h 2p k m = n + 1 2 æ è ö ø h ×nclassical Vibrational quantum number (0, 1, 2. ) E0 = 1 2 hnclassical Ground vibrational state (n = 0) E1 = 3 2 hnclassical First excited state (n = 1) DE = hnclassical Calculated DE often agrees quite well with experiment ncalculated (C=O) = 1600 cm-1 nexperiment (C=O) = 1600-1800 cm-1 See example 16-1 (2) Dn = ±1 Vibrational Selection Rule Since levels equally spaced - should see one absorption frequency CEM 333 page 6.7
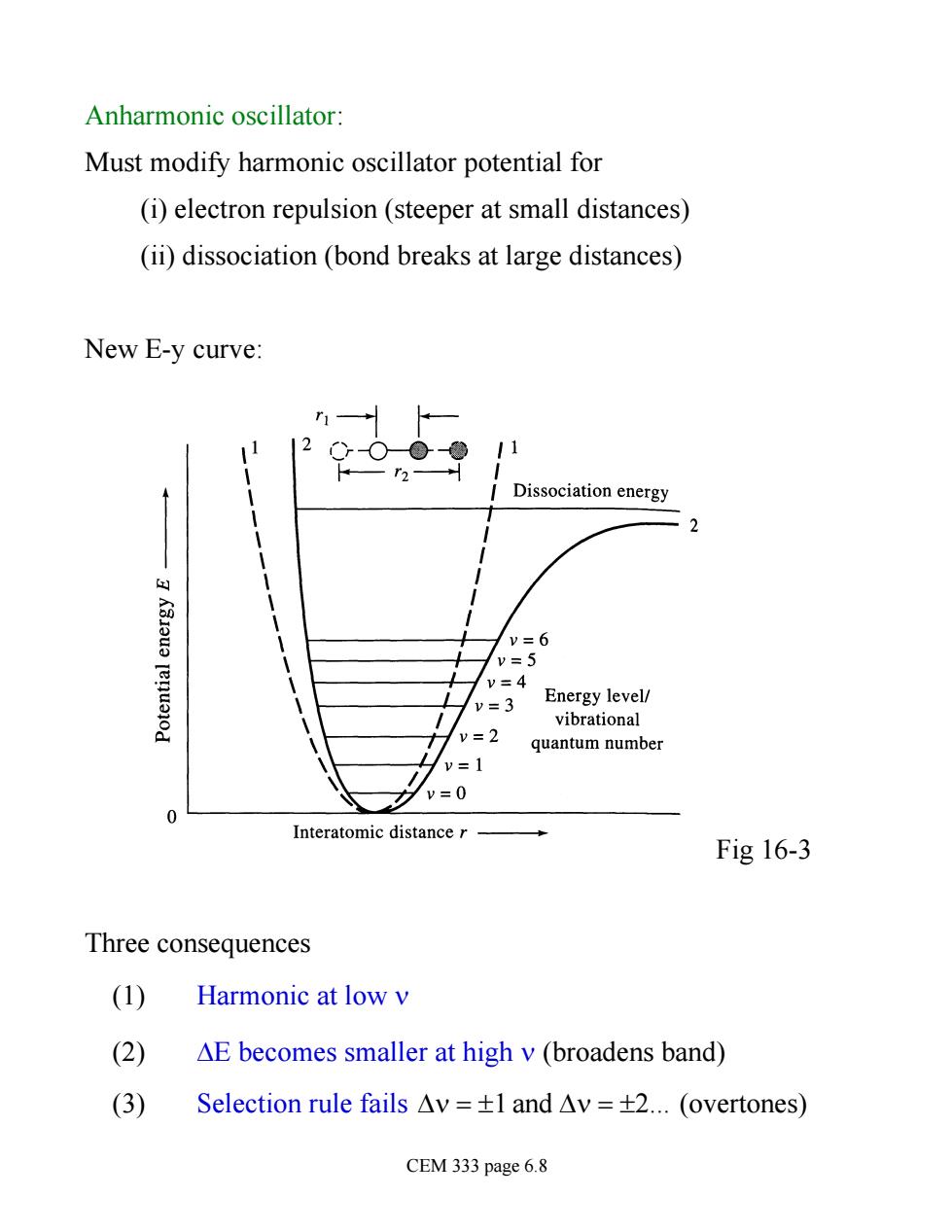
Anharmonic oscillator: Must modify harmonic oscillator potential for (i)electron repulsion(steeper at small distances) (ii)dissociation (bond breaks at large distances) New E-y curve: r1 11 Dissociation energy -2 y=6 v=5 v=4 v=3 Energy level/ vibrational y=2 quantum number =1 v=0 Interatomic distance r Fig 16-3 Three consequences (1) Harmonic at low v (2) AE becomes smaller at high v(broadens band) (3) Selection rule fails△v=±land△v=±2.(overtones) CEM 333 page 6.8
Anharmonic oscillator: Must modify harmonic oscillator potential for (i) electron repulsion (steeper at small distances) (ii) dissociation (bond breaks at large distances) New E-y curve: Fig 16-3 Three consequences (1) Harmonic at low n (2) DE becomes smaller at high n (broadens band) (3) Selection rule fails Dn = ±1 and Dn = ±2. (overtones) CEM 333 page 6.8