
Introduction to Atomic Optical Spectroscopy (Chapter 8) Sample is atomized (atoms/ions) absorption or emission measured Energy Level Diagrams Every elements has unique set of atomic orbitals p,d,f.levels split by spin-orbit coupling Spin(s)and orbital (1)motion create magnetic fields that perturb each other (couple) if fields parallel-slightly higher energy if fields antiparallel-slightly lower energy N N VS. N Define SO coupling by J(total angular momentum) J=L+S(L=ΣlS=Σs)(positive values only) CEM 333 page 7.1
Introduction to Atomic Optical Spectroscopy (Chapter 8) Sample is atomized (atoms/ions) absorption or emission measured Energy Level Diagrams Every elements has unique set of atomic orbitals p,d,f. levels split by spin-orbit coupling Spin (s) and orbital (l) motion create magnetic fields that perturb each other (couple) if fields parallel - slightly higher energy if fields antiparallel - slightly lower energy N S N S vs. N S S N Define SO coupling by J (total angular momentum) J=L+S (L = ål S = ås) (positive values only) CEM 333 page 7.1

Example: s electron(1=0,s=+1/2or-1/2)J=0+1/2=l/2 p electron (1=1,s=+1/2 or-1/2)J=1+1/2=3/2(higher energy)or 1-1/2=1/2 (lower energy) Electronic Term Symbol 2+LLwritten as letter(S,P,D.)instead of number! Li=1s22s! L=0,S=±1/22S12 Li*=1s22p L=1,S=t1/22P32,12 Be =1s22s2 L=0,S=0 1S Be*=1s22s2p1L=1,S=1,03P2,1P0 CEM 333 page 7.2
Example: s electron (l=0, s=+1/2 or -1/2) J=0+1/2=1/2 p electron (l=1, s=+1/2 or -1/2) J=1+1/2=3/2 (higher energy) or 1-1/2=1/2 (lower energy) Electronic Term Symbol 2S+1LJ L written as letter (S, P, D.) instead of number! Li =1s2 2s1 L = 0, S = ±1 / 2 2 S1/2 Li* =1s2 2p1 L = 1, S = ±1 / 2 2 P3/2,1/2 Be =1s2 2s2 L = 0, S = 0 1 S0 Be* =1s2 2s1 2p1 L =1, S = 1, 0 3 P2 , 1 P0 CEM 333 page 7.2
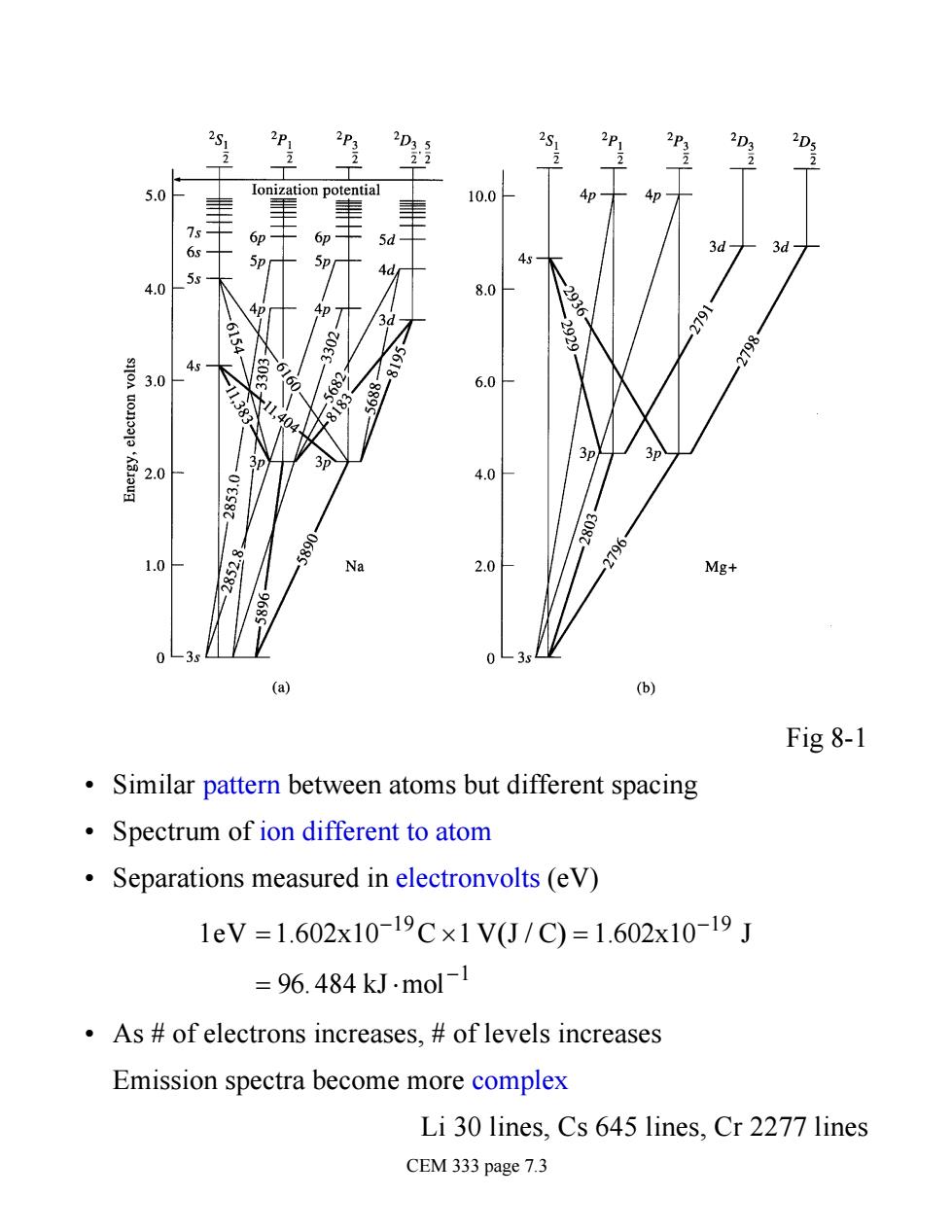
3P: D lonization potential 10.0 5d d 43 4.0 8.0 4p- 号30 45 682 81 20 2.0 Mg+ 0-3 (a) (b) Fig 8-1 Similar pattern between atoms but different spacing Spectrum of ion different to atom Separations measured in electronvolts (eV) 1eV=1.602x10-19c×1VJ/C)=1.602x10-19J =96.484 kJ.mol-1 As of electrons increases,of levels increases Emission spectra become more complex Li 30 lines,Cs 645 lines,Cr 2277 lines CEM 333 page 7.3
Fig 8-1 • Similar pattern between atoms but different spacing • Spectrum of ion different to atom • Separations measured in electronvolts (eV) 1eV =1.602x10-19C´1 V(J / C) = 1.602x10-19 J = 96. 484 kJ×mol-1 • As # of electrons increases, # of levels increases Emission spectra become more complex Li 30 lines, Cs 645 lines, Cr 2277 lines CEM 333 page 7.3

Desire narrow lines for accurate identification Broadened by (i)uncertainty principle (ii)pressure broadening (iii)Doppler effect (iv)(electric and magnetic fields) Atomic line widths: (i)Uncertainty Principle: Quantum mechanical idea states must measure for some minimum time to tell two frequencies apart △t·△E≥h △t △y≥1 minin measurement difference in frequencies Shows up in lifetime of excited state if lifetime infinitely long,AE infinitely narrow ·if lifetime short,△E is broadened CEM 333 page 7.4
Desire narrow lines for accurate identification Broadened by (i) uncertainty principle (ii) pressure broadening (iii) Doppler effect (iv) (electric and magnetic fields) Atomic line widths: (i) Uncertainty Principle: Quantum mechanical idea states must measure for some minimum time to tell two frequencies apart Dt×DE ³ h Dt minimum time for measurement { × Dn minimum detectable difference in frequencies { ³1 Shows up in lifetime of excited state • if lifetime infinitely long, DE infinitely narrow • if lifetime short, DE is broadened CEM 333 page 7.4
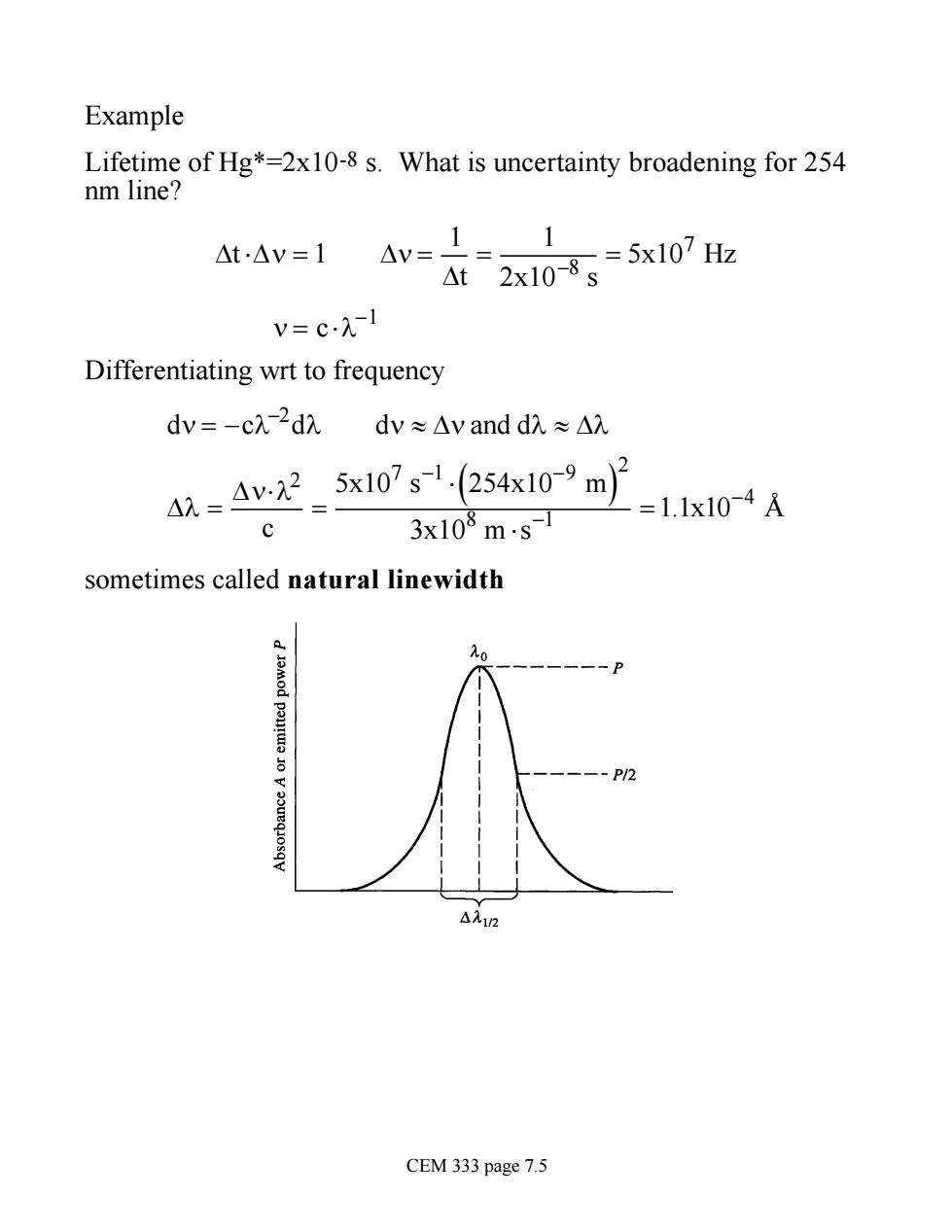
Example Lifetime of Hg*=2x10-8 s.What is uncertainty broadening for 254 nm line? At-Av=1 Av=1= At2x10-8g=5x107z 1 V=cλ-1 Differentiating wrt to frequency dv=-cλ-2ddv≈△y and dA≈△ .=4v22_5x107s1(254x10-9m2 3x108m.s-1 =1.1x104A c sometimes called natural linewidth △入12 CEM 333 page 7.5
Example Lifetime of Hg*=2x10-8 s. What is uncertainty broadening for 254 nm line? Dt ×Dn = 1 Dn = 1 Dt = 1 2x10-8 s = 5x107 Hz n = c ×l-1 Differentiating wrt to frequency dn = -cl -2 dl dn » Dn and dl » Dl Dl = Dn×l2 c = 5x107 s -1 × 254x10-9 ( m) 2 3x108 m ×s -1 =1.1x10-4 Å sometimes called natural linewidth CEM 333 page 7.5