
第1章质点力学 由初始运动条件 x=X0,y=y0,2=20 t=0, 元=ox,y=0y,2=o: x=xo+d,y=yo+yd,==zo+idt Vs Yos +f dt,Vy Voy +fdt,v.Voz +dt
第1章 质点力学 由初始运动条件 = = = = = = = x y z x v y v z v x x y y z z t 0 0 0 0 0 0 , , , , 0, = + = + = + t t t x x xdt y y ydt z z zdt 0 0 0 0 0 0 , , = + = + = + t z z t y y t vx v x xdt v v ydt v v zdt 0 0 0 0 0 0 , ,
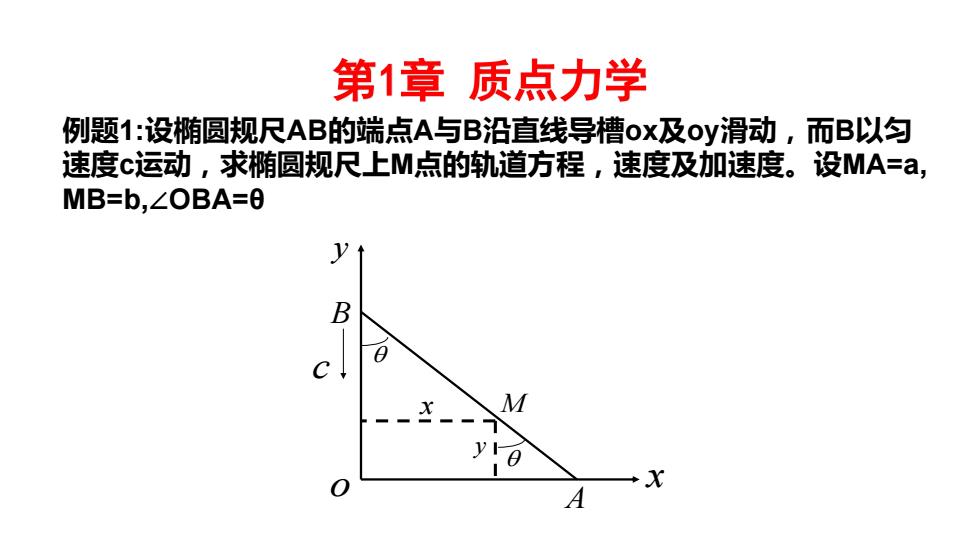
第1章质点力学 例题1:设椭圆规尺AB的端点A与B沿直线导槽ox及oy滑动,而B以匀 速度c运动,求椭圆规尺上M点的轨道方程,速度及加速度。设MA=a, MB=b,∠OBA=0 M +x A
第1章 质点力学 例题1:设椭圆规尺AB的端点A与B沿直线导槽ox及oy滑动,而B以匀 速度c运动,求椭圆规尺上M点的轨道方程,速度及加速度。设MA=a, MB=b,∠OBA=θ o x y A M B c x y

第1章质点力学 x=bsin 0 坐标关系 y=acose 轨道方程】 B 结论:轨道为以原点为中心,以坐标轴为对称轴的椭圆 速度 -龙一 x=be cos0 i=-a0sin0 A 由B点运动约束:V=少g=-(a+b)0sin0=-c 得 = a+b sin 0 因此得:=be coto-ae a+b √a2+b2cot0 a+b 又可得:=- (a+b)=、 be2 (a+br=0aw=Ve+评=bc21 b4c21 (a+b)2x3
第1章 质点力学 坐标关系 = = cos sin y a x b 轨道方程 结论:轨道为以原点为中心,以坐标轴为对称轴的椭圆 速度 由B点运动约束: v y a b c B = B = −( + ) sin = − 得 : sin 1 a b c + = 因此得: cot, , cot 2 2 a b a b c v a b ac y a b bc x M + + = + = − + = 又可得: , 0 1 ( ) csc ( ) 2 3 4 2 3 2 2 = + = − + = − y a b x b c a b bc x 2 3 4 2 2 2 1 (a b) x b c a x y M + = + = o x y A M B c x y sin y = −a
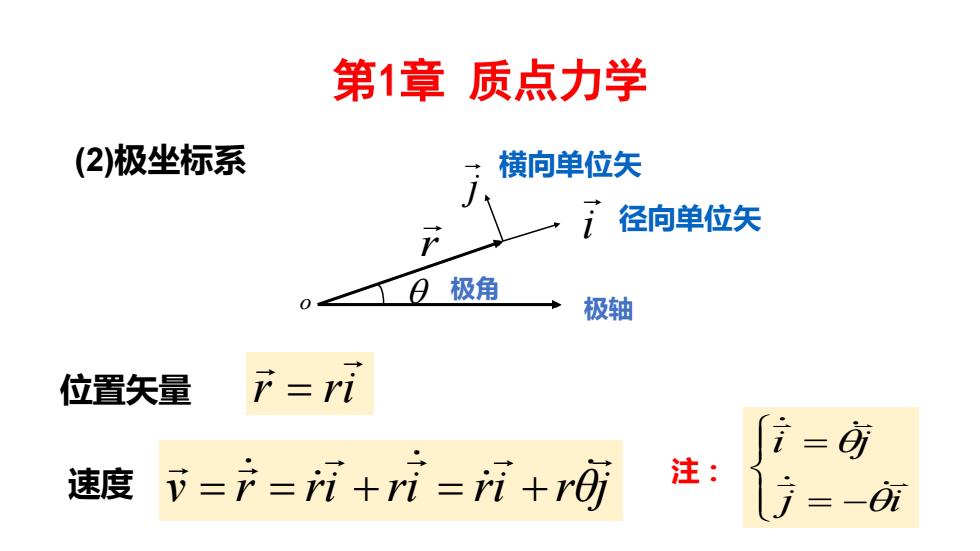
第1章质点力学 (2)极坐标系 横向单位矢 径向单位矢 日极角 0 极轴 位置矢量 r=ri =疬 速度 下=产=ri+ri=i+r 注: 方=-航
第1章 质点力学 (2)极坐标系 r ri = v r ri ri ri rθj 速度 = = + = + 位置矢量 = − = j i i j 注: r i j 径向单位矢 横向单位矢 o 极轴 极角

第1章质点力学 V.=F 径向速度 速度 g=r0 横向速度 加速度a==(-r0)i+(r0+20) a=护-r02 径向加速度 = a,=ri+2r0=1d20 注: 横向加速度 方=- r dt
第1章 质点力学 = = v r v r r 速度 a v r r i r r j ( ) ( 2 ) 2 = = − + + = + = − a r r a r r r 2 2 径向速度 横向速度 径向加速度 横向加速度 = − = j i i j 注: 加速度 ( ) 1 2 r dt d r =