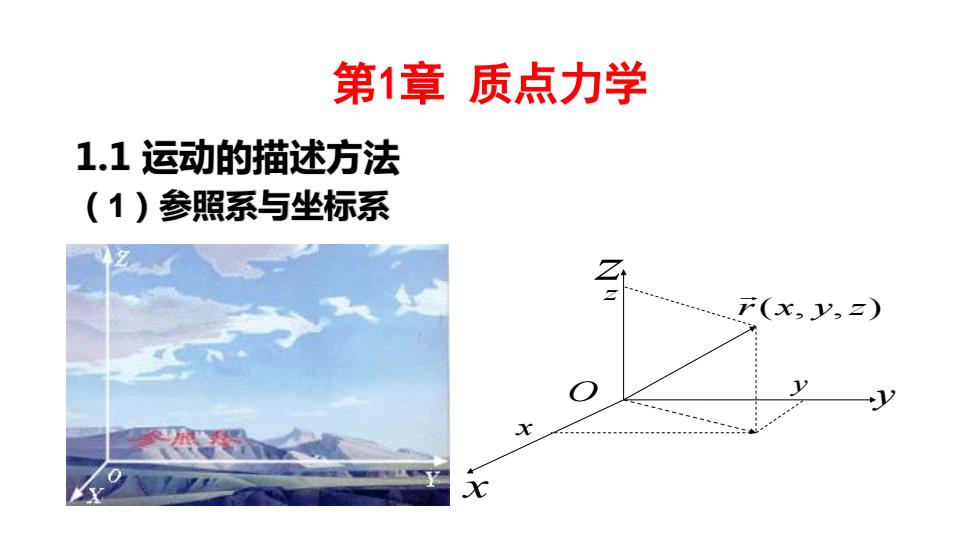
第1章质点力学 1.1运动的描述方法 (1)参照系与坐标系 r(x,y,z)
第1章 质点力学 1.1 运动的描述方法 (1)参照系与坐标系 O x y z r(x, y,z) x y z
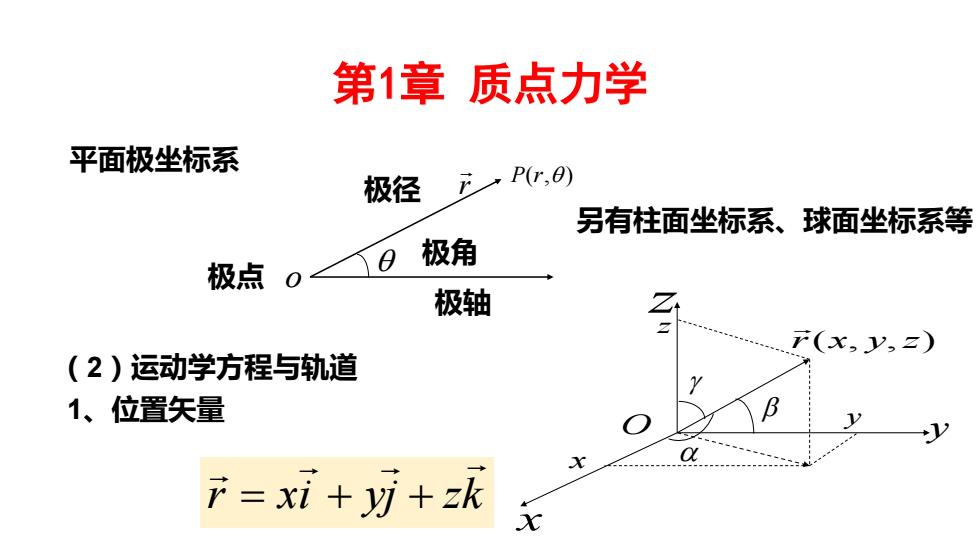
第1章质点力学 平面极坐标系 极径 FP,) 另有柱面坐标系、球面坐标系等 极角 极点 极轴 r(x,y,Z) (2)运动学方程与轨道 1、位置矢量 F=xi+万+zk
第1章 质点力学 平面极坐标系 o r P(r,) 极点 极轴 极径 极角 另有柱面坐标系、球面坐标系等 (2)运动学方程与轨道 1、位置矢量 r xi yj zk = + + O x y z r(x, y,z) x y z

第1章质点力学 方向角与方向余弦 a,B,Y cosa,cos B,cosy 方向余弦满足 cos2 a+cos2 B+cos2y=1 2、运动学方程 x=x(t) r=r(t) 矢量形式 下=F() 坐标形式 y=y(t) 2=z(t) 10=0(t)
第1章 质点力学 2、运动学方程 r r(t) = = = = ( ) ( ) ( ) z z t y y t x x t = = ( ) ( ) t r r t 方向角与方向余弦 cos ,cos ,cos , , 方向余弦满足 cos cos cos 1 2 2 2 + + = 矢量形式 坐标形式

第1章质点力学 3、轨道方程(单值连续) 空间曲线:y=∫(z,x),z=g(x,y) 平面曲线:y=f(x),r=g(0). (3)位移、速度和加速度 位移 F=r(t+t)-(t)=△xi+△y+△k 速度 =产=x就+访+讯 dt 加速度 dv a= d'r dt dt2 =芹=就++讯
第1章 质点力学 3、轨道方程(单值连续) 空间曲线: 平面曲线: y = f (x),r = g( ). (3)位移、速度和加速度 位移 Δr r t Δt r t xi yj zk = ( + ) − ( ) = + + 速度 r xi yj zk dt dr v = = = + + 加速度 r xi yj zk dt d r dt dv a = = = = + + 2 2

第1章质点力学 1.2速度、加速度的分量表示 (1)直角坐标系 速度 i=Vi+vyj+vh Vx=x,y,=,V:=2 加速度i=a,i+a,j+a.kax=龙,a,=立,a=艺
第1章 质点力学 1.2 速度、加速度的分量表示 (1)直角坐标系 速度 v v i v j v k x y z = + + v x v y v z x y z = , = , = 加速度 a a i a j a k x y z = + + a x a y a z x y z = , = , =