
截断型维里方程 般情况 Z=1+BP 当 B V Z=1+Bp+Cp 当 B C 维里方程的优点:(1)物理意义明确, (2)实验曲线拟合容易
截断型维里方程 当 1 B Z v = + 一般情况 1 2 c ' Z B p = +1 当 2 1 B C Z v v = + + 1 2 c c ' ' 2 Z B p C p = + + 1 维里方程的优点:(1)物理意义明确, (2)实验曲线拟合容易

临界温度: -122.4℃(150.7K);临界压力:4864kPa 临界密度: 530.7kg/m3 50 3000 0 2500 2000 -50 150 1000 500 6 200- -250 Ar -500 Ar 300 -1000 200 400 600 800 1000 200 400 600 800 T/K T/K 第二维里系数在低温区具有很大的负值,但在高温区为很小的正值,若无限高温时流体接 近理想气体性质从而B(T)趋近于零; 第三维里系数在临界点附近具有一个正的峰值,随着温度降低,C(T))迅速减小,在低温区 变为负值,而随着温度升高,C(T)一直为正并平缓趋近于零
11 第二维里系数在低温区具有很大的负值,但在高温区为很小的正值,若无限高温时流体接 近理想气体性质从而 B (T)趋近于零; 第三维里系数在临界点附近具有一个正的峰值,随着温度降低,C(T) 迅速减小,在低温区 变为负值,而随着温度升高,C(T) 一直为正并平缓趋近于零。 临界温度: -122.4℃ (150.7 K);临界压力:4864 kPa 临界密度: 530.7 kg/m3 Ar Ar

经验性状态方程 几百种状态方程 范围广,精度差 范围窄,精度高 提出最早,影响最大:范德瓦尔斯方程 Van der Waals equation 1873年提出,从理想气体假设的修正出发
范围广,精度差 范围窄,精度高 经验性状态方程 提出最早,影响最大:范德瓦尔斯方程 几百种状态方程 1873年提出,从理想气体假设的修正出发 Van der Waals equation

二常数半经验方程 ■范德瓦尔斯方程 RK方程(1949年瑞里奇-邝) RKS方程 RKS的其他形式 ■PR方程
二常数半经验方程 ◼ 范德瓦尔斯方程 ◼ RK方程 (1949年瑞里奇-邝) ◼ RKS方程 ◼ RKS的其他形式 ◼ PR方程
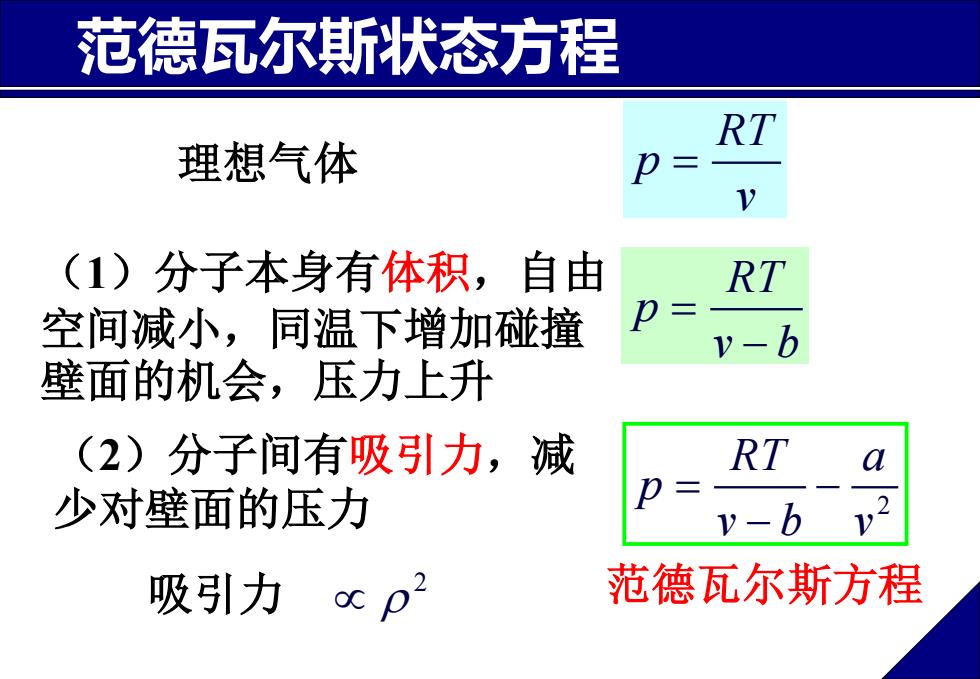
范德瓦尔斯状态方程 RT 理想气体 p (1)分子本身有体积,自由 RT 空间减小,同温下增加碰撞 v-b 壁面的机会,压力上升 (2)分子间有吸引力,减 RT a 少对壁面的压力 v-b 吸引力 范德瓦尔斯方程
范德瓦尔斯状态方程 (1)分子本身有体积,自由 空间减小,同温下增加碰撞 壁面的机会,压力上升 理想气体 (2)分子间有吸引力,减 少对壁面的压力 RT p v = RT p v b = − 吸引力 2 2 RT a p v b v = − − 范德瓦尔斯方程