
KAc()a(Ae)(HAe) Ka [HAc] a(HAc) r(Ac)(Ac) pKM=4.65(I=0.1) HAc:KC>KM>K 上述规律适用于任何一元弱酸吗? 11
11 M a H [Ac ] (H ) (Ac ) (HAc) a [HAc] (HAc) (Ac ) (Ac ) a a a K K a + − + − − − = = = ( )M p 4.65 a K = ( 0.1) I = C M HA a a a c : K K K 上述规律适用于任何一元弱酸吗?
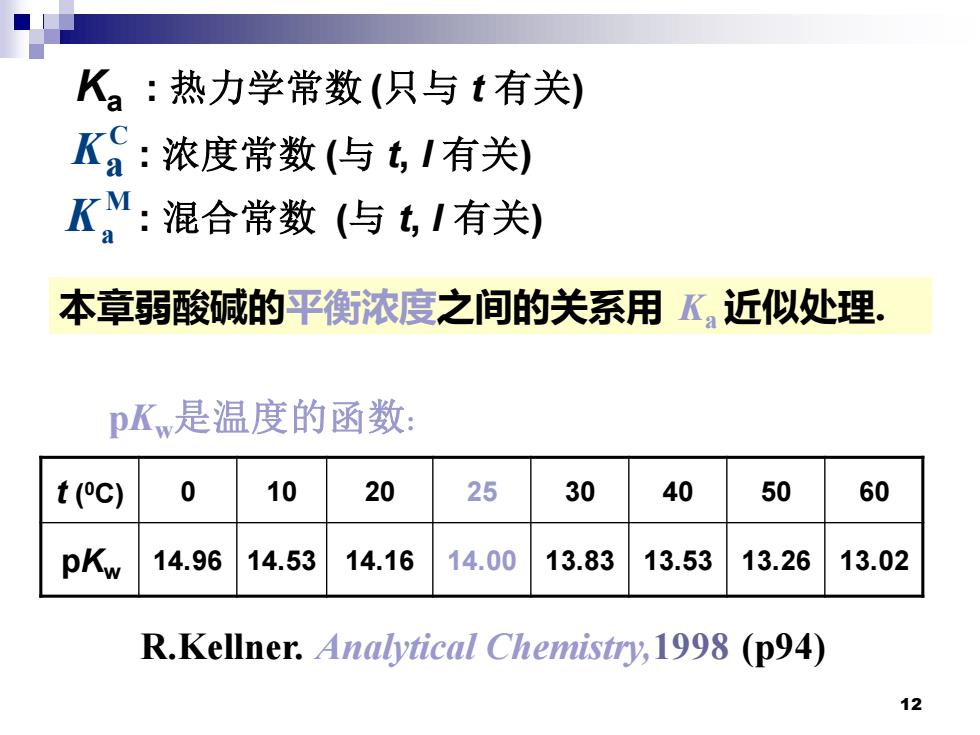
K:热力学常数(只与t有关) K:浓度常数(与,I有关) K:混合常数(与tI有关) 本章弱酸碱的平衡浓度之间的关系用K,近似处理。 pKw是温度的函数: t(C) 0 10 20 25 30 40 50 60 pKw 14.96 14.53 14.16 14.00 13.83 13.53 13.26 13.02 R.Kellner.Analytical Chemistry,1998 (p94) 12
12 Ka : 热力学常数 (只与 t 有关) : 浓度常数 (与 t, I 有关) : 混合常数 (与 t, I 有关) t ( 0C) 0 10 20 25 30 40 50 60 pKw 14.96 14.53 14.16 14.00 13.83 13.53 13.26 13.02 C Ka M Ka pKw是温度的函数: R.Kellner. Analytical Chemistry,1998 (p94) 本章弱酸碱的平衡浓度之间的关系用 Ka 近似处理

4.2 酸度对弱酸(碱)形态分布的影响 4.2.1一元弱酸的摩尔分数 x(HA)=HA [HA] [H] [HA+[A】HI+Ka (A)=A1三 [A] Ka [HA+[A】H]+Ka x(HA)+x(A)=1 [HA=C.x(HA),A=c.x(A) “x”将平衡浓度与分析浓度联系起来。 13
13 a [HA] [HA] (HA) [HA [ H ] [A ] ] [H ] x c K + − + = + + = = - a a [A ] [A ] (A ) [HA] [A ] [H ] K K x c − + − − = = + = + 4.2 酸度对弱酸(碱)形态分布的影响 4.2.1 一元弱酸的摩尔分数 - - - ( HA ) (A ) 1 [HA] ( HA ), [ A ] ( A ) x x c x c x + = = = “x” 将平衡浓度与分析浓度联系起来

例1计算pH=4.00和8.00时的xHAc)、x(Ac) 解:已知HAc的K=1.75X10-5 pH=4.00时 [H"] x(HAc)= =0.85 H]+K, x(Ac-)= K。 =0.15 H]+K, pH=8.00时x(HAc)=5.7×10-4,x(Ac)≈1.0 14
14 例1 计算pH=4.00和8.00时的x(HAc)、x(Ac- ) 解: 已知HAc的Ka=1.75×10-5 pH = 4.00时 a [H ] [H ] x(HAc) 0.85 K + + + = = pH = 8.00时 x(HAc) = 5.7×10-4 , x(Ac- ) ≈ 1.0 a a [H ] x(Ac ) 0.15 K K − + + = =

不同pH下的xHA)与x(A) pH x(HA) x(A) pKa -2.0 0.99 0.01 *pK2-1.3 0.95 0.05 pK2-1.0 0.91 0.09 **pKa 0.50 0.50 pK2+1.0 0.09 0.91 *pK2+1.3 0.05 0.95 pK2+2.0 0.01 0.99 以x,xo对pH作图,即可得形态分布图. 15
15 pH x(HA) x(A- ) pKa - 2.0 0.99 0.01 *pKa - 1.3 0.95 0.05 pKa - 1.0 0.91 0.09 **pKa 0.50 0.50 pKa + 1.0 0.09 0.91 *pKa + 1.3 0.05 0.95 pKa + 2.0 0.01 0.99 以x1 , x0 对pH 作图, 即可得形态分布图. 不同pH下的x(HA) 与x(A- )