
第六章 种用价值的评定 基因型选择 甘肃农业大学动物科学技术学院 2023/5/23
2023/5/23 1 第六章 种用价值的评定 ——基因型选择 甘肃农业大学动物科学技术学院

>基因型选择是以表型选择为基础,根据被选对象本身或其祖先、 同胞及后裔的遗传性能表现进行选择。 >基因型选择,若为质量性状,则可根据简单的孟德尔定律进行遗 传分析,判断基因型,选择比较容易;若为数量性状,由于正确判 断其基因型比较困难,所以必须根据被选个体本身及其祖先、同胞 和后裔的表型值来预测育种值,然后根据育种值的大小进行选择。 2023/5/23 2
2023/5/23 2 ➢基因型选择是以表型选择为基础,根据被选对象本身或其祖先、 同胞及后裔的遗传性能表现进行选择。 ➢基因型选择,若为质量性状,则可根据简单的孟德尔定律进行遗 传分析,判断基因型,选择比较容易;若为数量性状,由于正确判 断其基因型比较困难,所以必须根据被选个体本身及其祖先、同胞 和后裔的表型值来预测育种值,然后根据育种值的大小进行选择

一、育种值的概念和特征 1、基因型值和群体均值的关系 对于式PG叶E: 在作为整体看待的群体中,环境影响有好有坏,但平均环境离差为零, 因而一个群体的平均表型值等于其平均基因型值。 为便于分析,以一个位点对表型值的影响来说明不同基因型值和群体 平均表型值的关系。 假设位点A上有一对等位基因A1与A2,A1A1的基因型值为+a,A2A2的基 因型值为-a(无论A1A1与A2A2的实际值是多少,在两个值的均数为0的情 况下,都可以用相等的绝对值来代表两者),A1A2的基因型值为d 基因型 A2A2 A1A2 A1A1 基因型值-a d +a 任意指定的基因型值 图中坐标原点,即零值点,位于两纯合体数值的中点上。A1A2的基因型值取 决于显性度(degree of dominance),即a/d,若没有显性,d0;若A1对A2 为显性,d值为正;若A2对A1为显性,d值为负;当显性完全时,a±a。 2023/5/23
2023/5/23 3 对于式P=G+E : 在作为整体看待的群体中,环境影响有好有坏,但平均环境离差为零, 因而一个群体的平均表型值等于其平均基因型值。 为便于分析,以一个位点对表型值的影响来说明不同基因型值和群体 平均表型值的关系。 假设位点A上有一对等位基因A1与A2,A1A1的基因型值为+a,A2A2的基 因型值为-a(无论A1A1与A2A2的实际值是多少,在两个值的均数为0的情 况下,都可以用相等的绝对值来代表两者),A1A2的基因型值为d 基因型 A2A2 A1A2 A1A1 –––|–––––––––––––––––|–––––––|––––––––––|––– 基因型值 -a 0 d +a 任意指定的基因型值 图中坐标原点,即零值点,位于两纯合体数值的中点上。A1A2的基因型值取 决于显性度(degree of dominance),即a/d,若没有显性,d=0;若A1对A2 为显性,d值为正;若A2对A1为显性,d值为负;当显性完全时,d=±a。 一、育种值的概念和特征 1、基因型值和群体均值的关系
又设群体中基因A的频率为p,A的频率为q,那么,三种基因型的频率 乘以相应的基因型值之和,就是群体均数。 一个座位两等位基因平均数的计数 基因型 频率 基因型值 群体均值 AA 2 +a pa AA2 2pq d 2pqd A2A2 g -a -da M p2a+2pqd-g2a a(p2-g2)+2pqd a(p+q)(p-q)+2pqd ∴.M=a(p-q)+2dpg 式中: a一以显性纯合子基因型值与隐性纯合子基因型值之均数为0点时的 显性纯合子基因型值; d—杂合子基因型值; Q 显性基因频率; 隐性基因频率。 从多位点来观察,如果不存在位点间的相互作用,则群体均值 2023/5/23 为: M=Σa(p-q)+2∑dpg
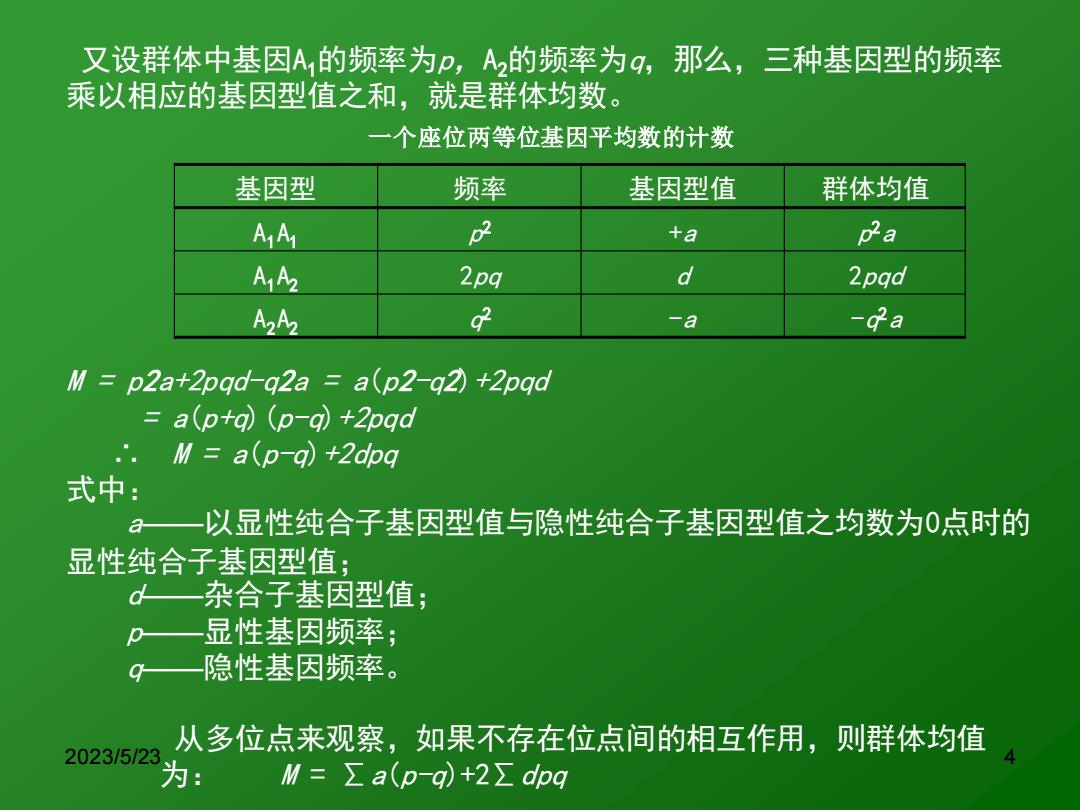
2023/5/23 4 又设群体中基因A1的频率为p,A2的频率为q,那么,三种基因型的频率 乘以相应的基因型值之和,就是群体均数。 一个座位两等位基因平均数的计数 基因型 频率 基因型值 群体均值 A1A1 p 2 +a p 2a A1 A2 2pq d 2pqd A2A2 q 2 -a -q 2a 从多位点来观察,如果不存在位点间的相互作用,则群体均值 为: M = ∑a(p-q)+2∑dpq M = p2a+2pqd-q2a = a(p2-q2)+2pqd = a(p+q)(p-q)+2pqd ∴ M = a(p-q)+2dpq 式中: a——以显性纯合子基因型值与隐性纯合子基因型值之均数为0点时的 显性纯合子基因型值; d——杂合子基因型值; p——显性基因频率; q——隐性基因频率

2、基因的平均效应 特定基因以随机方式与群体的基因样本相结合而形成合子的平均基 因型值对群体均值的离差,就是该基因在特定群体中的平均效应。 例如,基因A,在某个群体中的平均效应。假设这个群体在A位点有A1、A2 两个等位基因,其频率各为和9。基因A,以随机方式与这个群体的基因 相结合,势必产生AA与A,A,两种基因型;两种基因型的频率应当与群 体中两种基因的频率相等,也就是会产生比例为的AA1,比例为g的 A1A20 这些合子的均值为:patqd 与群体均值的离差则是:a1=pa+gd-[a(p-q)+2dpg] g[atd(g-p)] 如a=a+d(q-p),a1=qa p、q 分别代表群体中显性基因与隐性基 这就是基因A的平均效应。 因的频率; 可得A,的平均效应为: ad二分别代表显性纯合子与杂合子的基 因型值: a2 =pLatd(q-p)]=-pa a1- 显性基因(在群体中的)平均效应; 2023/5/23 a2— 隐性基因的平均效应
2023/5/23 5 2、基因的平均效应 特定基因以随机方式与群体的基因样本相结合而形成合子的平均基 因型值对群体均值的离差,就是该基因在特定群体中的平均效应。 例如,基因A1在某个群体中的平均效应。假设这个群体在A位点有A1、A2 两个等位基因,其频率各为p和q。基因A1以随机方式与这个群体的基因 相结合,势必产生A1A1与A1A2两种基因型;两种基因型的频率应当与群 体中两种基因的频率相等,也就是会产生比例为p的A1A1,比例为q的 A1A2。 这些合子的均值为:pa+qd; 与群体均值的离差则是:α1 = pa+qd-[a(p-q)+2dpq] = q[a+d(q-p)] 如α=a+d(q-p), α1 = qα 这就是基因A1的平均效应。 可得A2的平均效应为: α2 = - p[a+d(q-p)] =-pα p、q——分别代表群体中显性基因与隐性基 因的频率; a、d——分别代表显性纯合子与杂合子的基 因型值; α1 ——显性基因(在群体中的)平均效应; α2 ——隐性基因的平均效应