《大学物理》课程教学资源（教案讲义）ch2 牛顿运动定律与力学中的守恒定律

第2章牛顿运动定律与力学中的守恒定律 2.1牛顿运动定律 2.1.1几种常见的力 万有引力 1.万有引力 万有引力是指存在于任何两个物质质点之间的吸引力。 F=Gmme,其中G为普适常数一引力常最，而且 G-6.67-10N-mkg. 2.重力 如图21所示，考虑放在地面上的物体，选择与地心相对静 止的参照系，则有 F+N=F向心， F=F向心力)-N, F别=F向心)+P(重力 F≈P(重力) 忽略地球的自转效应时，重力就是地球对其表面上的物体产生的引力，其方向指向地心。 F=P=g,为物体在重力作用下具有的加速度，称为重力加速度。 赤道的重力加速度大还是两极的重力加速度大？为什么？ 当物体相对地球静止时，物体的重量和物体所受重力的量值相等。 弹性力 发生形变的物体，由于要恢复原状，对与它接触的物体会产生力 的作用，这种物体因形变而产生欲使其恢复原来形状的力叫做弹性 力。 常见的弹性力有 1.弹簧被拉伸或压缩时产生的弹簧弹性力，遵守胡克定律： 图2-2弹性力 了三-kx, x表示形变位移，k为弹簧的劲度系数。而弹簧弹性力的方向总口●=●。一下 是指向要恢复它原长的方向。 绳内部各段之间的弹性作用力，A点和B点的张口●。一 T=-TA.T8=-TB: 图23绳中张力 由牛顿第二定律： T4+T。=m, (1)当a0或者m一0时，T4=-TB=F,绳子上各点张力相同而 且拉力相等。 2)当a≠0而且m≠0（绳子质最不能忽略时）.绳子上各点的张 力不同

第 2 章 牛顿运动定律与力学中的守恒定律 2.1 牛顿运动定律 2.1.1 几种常见的力 万有引力 ⒈ 万有引力 万有引力是指存在于任何两个物质质点之间的吸引力。 r r m m F G e 2 1 2 = ，其中 G 为 普适 常数 —引 力常 量， 而且 G=6.67×10-11N·m2·kg-2 . 2．重力 如图 2-1 所示，考虑放在地面上的物体，选择与地心相对静 止的参照系，则有： 引 (向心力) F + N = Fn ， F引 = Fn (向心力) − N ， F引 = F (向心力) + P(重力) n ， F引  P(重力) 忽略地球的自转效应时，重力就是地球对其表面上的物体产生的引力，其方向指向地心。 F引 = P = mg .为物体在重力作用下具有的加速度，称为重力加速度。 【思考】 赤道的重力加速度大还是两极的重力加速度大？为什么？ 【注意】 重量与重力的区别： 当物体相对地球静止时，物体的重量和物体所受重力的量值相等。 弹性力 发生形变的物体，由于要恢复原状，对与它接触的物体会产生力 的作用，这种物体因形变而产生欲使其恢复原来形状的力叫做弹性 力。 常见的弹性力有： 1．弹簧被拉伸或压缩时产生的弹簧弹性力，遵守胡克定律： 图 2-2 弹性力 f = −kx， x 表示形变位移， k 为弹簧的劲度系数。而弹簧弹性力的方向总 是指向要恢复它原长的方向。 2．绳子被拉紧时所产生的张力 绳的张力—绳内部各段之间的弹性作用力，A 点和 B 点的张 力： A A T = −T' , B B T = −T' , 图 2-3 绳中张力 由牛顿第二定律： TA +T' B = ma ， （1）当 a=0 或者 m→0 时， TA = −T' B = F ，绳子上各点张力相同而 且拉力相等。 （2）当 a  0 而且 m  0 （绳子质量不能忽略时），绳子上各点的张 力不同。 O F引 P Fn N

(3)张力的大小取决于绳被拉紧的程度，它的方向总是沿着绳而指向绳要收缩的方向。 图24支撑力 3.物放在支承面上产生的正压力（作用在支承面上）和支持力（作用在物体上）.两个 物体相互接触且相互挤压时产生的，大小取决与相互挤压的程度，方向垂直与接触面指向对 方。 摩擦力 相对滑动趋势的接触力 Fm=4Fw,4。叫做静摩擦因数，它与两接触物体的材料性质 以及接触面的情况有关，而与接触面的大小无关。 2.当外力超过最大静摩擦力时，两相互接触的物体沿接触面 发生相对滑动，两物体的接触面间会出现一种阻碍相对滑动的接触 -滑动摩擦力。 图2.5康擅力 F。=FX,4叫做滑动摩擦因数，它与两接触物体的材料性质、接触表面的情况、温度、 干湿度等有关，还与两接触物体的相对速度有关。 物理学中的四种相互作用 现代物理学按物体之间相互作用性质可将力归结为四类： 力的种类 相互作用的物体 力的品度 力程 相互作用举例 轻子等 10时 小于10m 形 核 的 电磁力 电荷 102N 无限远 和原子核结合形成 强力 核子、介子等 10'N 10-15m 质子和中子结合形成原 子核 2.1.2、牛顿第一定律（惯性定律） 1.表述 任何物体都要保持其静止或匀速直线运动状态，直到外力迫使它改变运动状态为止。 数学表达式：没有外力作用时，v=恒矢量 【讨论】第一定律阐明了以下两个重要的力学基本概念： 一定律表明，任何物体都具有保持其运动状态不变的性质，这个性质叫做惯性 员性是物质的固有属性，它正是物质与运动不可分离的反映，它反映了物体政变运动状态的 第一定律还表明，正是由于物体具有惯性，所以要使物体的运动状态发生变化， 川做力。 力是使物体运动状态发生变化即使物体产生加速度的原因。但不是维持速度的原因。 (3)惯性参考系（惯性系）的概念 在这种参考系中观察，一个不受合外力作用的物体将保持静止和匀速直线运动状态不 变。 弱电统一理论“大统一理论“超统一理论” 2.13牛顿第二定律惯性质量引力质量 物体受到外力作用时，物体所获得的加速度的大小与合外力的大小成正比并与物体的质

9 9 图 2-5 摩擦力 （3）张力的大小取决于绳被拉紧的程度，它的方向总是沿着绳而指向绳要收缩的方向。 图 2-4 支撑力 3．物放在支承面上产生的正压力（作用在支承面上）和支持力（作用在物体上）．两个 物体相互接触且相互挤压时产生的，大小取决与相互挤压的程度，方向垂直与接触面指向对 方。 摩擦力 ⒈ 两相互接触的物体沿接触面有相对滑动趋势时，两物体的接触面间会出现一种阻碍 相对滑动趋势的接触力 —— 静 摩 擦 力 。 最 大静 摩 擦 力 ： F max =  0FN ,  0 叫做静摩擦因数，它与两接触物体的材料性质 以及接触面的情况有关，而与接触面的大小无关。 2．当外力超过最大静摩擦力时，两相互接触的物体沿接触面 发生相对滑动，两物体的接触面间会出现一种阻碍相对滑动的接触 力——滑动摩擦力。 F = FN ,  叫做滑动摩擦因数，它与两接触物体的材料性质、接触表面的情况、温度、 干湿度等有关，还与两接触物体的相对速度有关。 物理学中的四种相互作用 现代物理学按物体之间相互作用性质可将力归结为四类： 力的种类 相互作用的物体 力的强度 力程 相互作用举例 万有引力 一切质点 10-34N 无限远 恒星形成银河系 弱力 轻子等 10-34N 小于 10-34m 核 β 衰变的力 电磁力 电荷 102N 无限远 电子和原子核结合形成 原子 强力 核子、介子等 104N 10-15 m 质子和中子结合形成原 子核 2.1.2、牛顿第一定律（惯性定律） 1．表述 任何物体都要保持其静止或匀速直线运动状态，直到外力迫使它改变运动状态为止。 数学表达式： 没有外力作用时，v=恒矢量 【讨论】第一定律阐明了以下两个重要的力学基本概念： （1）第一定律表明，任何物体都具有保持其运动状态不变的性质，这个性质叫做惯性。 惯性是物质的固有属性，它正是物质与运动不可分离的反映，它反映了物体改变运动状态的 难易程度。 （2）第一定律还表明，正是由于物体具有惯性，所以要使物体的运动状态发生变化， 一定要有其它物体对它作用，这种作用叫做力。 力是一个物体对另一个物体的作用； 力是使物体运动状态发生变化即使物体产生加速度的原因。但不是维持速度的原因。 （3）惯性参考系（惯性系）的概念 在这种参考系中观察，一个不受合外力作用的物体将保持静止和匀速直线运动状态不 变。 弱电统一理论“大统一理论”“超统一理论” 2.1.3 牛顿第二定律 惯性质量 引力质量 物体受到外力作用时，物体所获得的加速度的大小与合外力的大小成正比并与物体的质

10 量成反比，加速度的方向与合外力的方向相同。表达式： F=平-d(mm) 2.用加度表示的牛第二定律=m.当宏发物体在低情况下是动时，即K心 时，上式可写成F=md业 =m0 这就是以往的第二定律表达式，但它是有局限性的，而动量表达式则具有普遍性。 3质量的物理意义 由牛顿第二定律可知，质量大的物体抵抗运动变化的性质强，也就是它的惯性大。所以 说，质量是物体惯性大小的量度。因此牛顿第二定律中的质量为惯性质量。 4.讨论 )第二定律说明力的瞬时效应。力和加速度同时产生，同时变化，同时消失，无先 后之分。 (2) 应理解为合外力，满足叠加原理。 (3)求解力学问题时，常应用分量式：F=ma,F,=ma,F=ma (4)牛顿第二定律只适用于质点，而且只适用于惯性系。 2.1.4牛顿第三定律 (又称为作用与反作用定律) 1.表述两个物体之间的作用力和反作用力，沿同一直线，大小相等，方向相反，分别 作用在两个物体上。 2.表达式F=-F。 孤立地存在。 力和反作用力总是属于同种性质 ”【注意]牛顿三大定律只适用于宏观、低速领域，当物体的运动速度接近光速或研究微 观客体的运动时，需要分别应用相对论力学和量子力学规律。 2.1.5牛顿定律的应用 应用牛顿定律解题步骤： 1.认真分析题意，确定研究对象。 先要弄清楚题目要求什么，确定研究对象，分析己知条件。 天列 ”进行运动分析。 包括它的轨迹、速度和加速度。涉及到几个物体时， 的关 出研究对象所受的所有外 析图。 分采用隔离体法”对其进行正确的受力分析，画出受力分 所谓隔离体法”就是把研究对象从与之相联系的其他物体中“隔离”出来，再把作用在此 物体上的力一个不漏地画出来，并正确地标明力的方向。 4.选取合适坐标，正确列出方程。 依据题目具体条件选好坐标系，然后把上面分析出的质量、加速度和力用牛顿运动定律 联系起来列出每一隔离体的运动方程的矢量式和分量式以及其他必要的辅助性方程，所列方 程总数应与未知量的数目相匹配 解列药是所，益后代入具体数据得出结果，最后进行必要的时 常力作用下的连结体问题

10 10 量成反比，加速度的方向与合外力的方向相同。表达式： t m t d d( ) d dp v F = = . 2．用加速度表示的牛顿第二定律 p = mv . 当宏观物体在低速情况下运动时，即 v<<c 时，上式可写成 a v F m t = m = d d . 这就是以往的第二定律表达式，但它是有局限性的，而动量表达式则具有普遍性。 3．质量的物理意义 由牛顿第二定律可知，质量大的物体抵抗运动变化的性质强，也就是它的惯性大。所以 说，质量是物体惯性大小的量度。因此牛顿第二定律中的质量为惯性质量。 4．讨论 （1）第二定律说明力的瞬时效应。力和加速度同时产生，同时变化，同时消失，无先 后之分。 （2） 应理解为合外力，满足叠加原理。 （3）求解力学问题时，常应用分量式： Fx = max , Fy = may , F z = maz . （4）牛顿第二定律只适用于质点，而且只适用于惯性系。 2.1.4 牛顿第三定律 （又称为作用与反作用定律） 1．表述．． 两个物体之间的作用力和反作用力，沿同一直线，大小相等，方向相反，分别 作用在两个物体上。 2．表达式 ．．． F = −F' . 【讨论】作用力和反作用力具有的特点 （1）作用力 F 和反作用力 − F' 总是成对出现，同时存在，同时消失，任何一方都不能 孤立地存在。（2）作用力和反作用力是分别作用在两个物体上的，不能相互抵消。（3）作用 力和反作用力总是属于同种性质的力。 【注意】牛顿三大定律只适用于宏观、低速领域，当物体的运动速度接近光速或研究微 观客体的运动时，需要分别应用相对论力学和量子力学规律。 2.1.5 牛顿定律的应用 应用牛顿定律解题步骤： ⒈ 认真分析题意，确定研究对象。 先要弄清楚题目要求什么，确定研究对象，分析已知条件。 2．明确物理关系，进行运动分析。 弄清物理过程，即分析对象的运动状态，包括它的轨迹、速度和加速度。涉及到几个物体时， 还要找出它们的速度或加速度之间的关系。 3．隔离研究对象，进行受力分析。 找出研究对象所受的所有外力，采用“隔离体法”对其进行正确的受力分析，画出受力分 析图。 所谓“隔离体法”就是把研究对象从与之相联系的其他物体中“隔离”出来，再把作用在此 物体上的力一个不漏地画出来，并正确地标明力的方向。 4．选取合适坐标，正确列出方程。 依据题目具体条件选好坐标系，然后把上面分析出的质量、加速度和力用牛顿运动定律 联系起来列出每一隔离体的运动方程的矢量式和分量式以及其他必要的辅助性方程，所列方 程总数应与未知量的数目相匹配。 5．求解所列方程，讨论所得结果。 解方程时，一般先进行文字符号运算，然后代入具体数据得出结果，最后进行必要的讨 论，判断结果是否合理。 1. 常力作用下的连结体问题

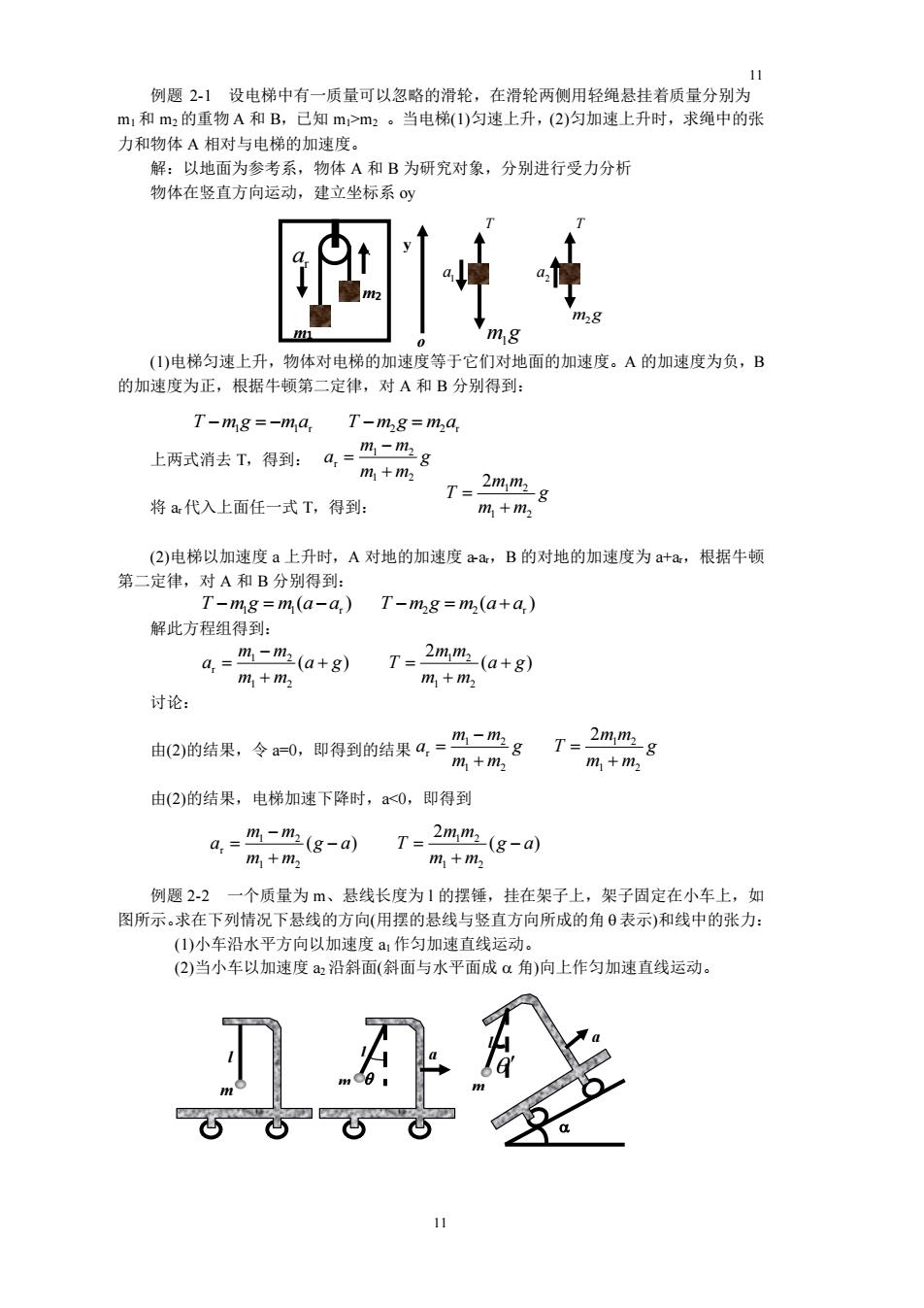
例愿2】设电梯中有一质量可以忽略的滑轮，在滑轮两侧用轻绳悬挂着质量分别为 m1和m2的重物A和B,已知m>m:。当电梯(1)匀速上升，(2)匀加速上升时，求绳中的张 力和物体A相对与电梯的加速度。 解：以地面为参考系，物体A和B为研究对象，分别进行受力分析 物体在竖直方向运动，建立坐标系y m.g ()电梯匀速上升，物体对电梯的加速度等于它们对地面的加速度。A的加速度为负，B 的加速度为正，根据牛顿第二定律，对A和B分别得到： T-mg=-ma,T-mg=ma 上两式消去，得到：4，+m 将a代入上面任一式T,得到： 1 (2)电梯以加速度a上升时，A对地的加速度aa,B的对地的加速度为a+a,根据牛顿 第二定律，对A和B分别得到： T-mg =m(a-a,) T-mg=m(a+a,) 解此方程组得到 a=m-m(a+g）T=2mm(a+g） m,+m, m+m 讨论： 由2)的结果，令0。即得到的结果Q,=%二m 7=2mm m+m %*%8 (2)的结果，电梯加速下降时，<0，即得到 a, m-mi (g-d)T=2mm -(g-a m +m m,+m 例题2-2 一个质量为m、悬线长度为1的摆锤，挂在架子上，架子固定在小车上，如 图所示。求在下列情况下悬线的方向（用摆的悬线与竖直方向所成的角6表示）和线中的张力： (1)小车沿水平方向以加速度：作匀加速直线运动。 (2)当小车以加速度沿斜面（斜面与水平面成α角）向上作匀加速直线运动

11 11 例题 2-1 设电梯中有一质量可以忽略的滑轮，在滑轮两侧用轻绳悬挂着质量分别为 m1 和 m2 的重物 A 和 B，已知 m1>m2 。当电梯(1)匀速上升，(2)匀加速上升时，求绳中的张 力和物体 A 相对与电梯的加速度。 解：以地面为参考系，物体 A 和 B 为研究对象，分别进行受力分析 物体在竖直方向运动，建立坐标系 oy (1)电梯匀速上升，物体对电梯的加速度等于它们对地面的加速度。A 的加速度为负，B 的加速度为正，根据牛顿第二定律，对 A 和 B 分别得到： 上两式消去 T，得到： 将 ar代入上面任一式 T，得到： (2)电梯以加速度 a 上升时，A 对地的加速度 a-ar，B 的对地的加速度为 a+ar，根据牛顿 第二定律，对 A 和 B 分别得到： 解此方程组得到： 讨论： 由(2)的结果，令 a=0，即得到的结果 由(2)的结果，电梯加速下降时，a<0，即得到 例题 2-2 一个质量为 m、悬线长度为 l 的摆锤，挂在架子上，架子固定在小车上，如 图所示。求在下列情况下悬线的方向(用摆的悬线与竖直方向所成的角  表示)和线中的张力： (1)小车沿水平方向以加速度 a1 作匀加速直线运动。 (2)当小车以加速度 a2 沿斜面(斜面与水平面成  角)向上作匀加速直线运动。 ar ar m1 m2 o y 1 a m 1 2 a m 2 m1 g m2 g T T T −m1g = −m1ar T −m2g = m2ar g m m m m a 1 2 1 2 r + − = g m m m m T 1 2 2 1 2 + = ( ) T −m1g = m1 a −ar ( ) T −m2g = m2 a + ar ( ) 1 2 1 2 r a g m m m m a + + − = ( ) 2 1 2 1 2 a g m m m m T + + = g m m m m a 1 2 1 2 r + − = g m m m m T 1 2 2 1 2 + = ( ) 1 2 1 2 r g a m m m m a − + − = ( ) 2 1 2 1 2 g a m m m m T − + = m l m l  a 1   m l a 2

12 解：D形小球为研疗对象当小车沿木平方作加速运动赋分析受力 方向小球加速度为 水平方向的加速度为。建立图示坐标系： 利用牛顿第二定律，列方程： x方向 Tsin 0=ma y方向：Tcos0-mg=0 解方程组，得到：了=mg+G g-9 0=ag马 (2)以小球为研究对象，当小车沿斜面作匀加速运动时，分析受力： 球的加速度沿斜面向上，垂直于斜面处于平衡状态，建立图示坐标系，重力与轴的夹 角为 用牛顿第二定律，列方程 14T2 T sina+)-mgsin a=ma T cos(a+0)-mgcosa=0 求解上面方程组，得到： T:=m(gsin a+a)+g'cos'a mg =m2gasin a+a+g a+)=&snatao arc sa+a - gcosa g cosa 讨论：如果α-0，=，则实际上是小车在水平方向作匀加速直线运动：如果a-0,加 速度为零，悬线保持在竖直方向。 例题23一重物m用绳悬起，绳的另一端系在天花板上，绳长0.5m,重物经推动后， 在一水平面内作匀速率圆周运动，转速=1s。这种装置叫做圆锥摆。求这时绳和竖直方向 所成的角度。 解：绳以小球为研究对象，对其进行受力分析 小球的运动情况，竖直方向平衡，水平方向作匀速圆周运动，建立坐标系如图： 拉力的沿两轴进行分解，竖直方向的分量与重力平衡，水平方向的分力提供向心力。利 用牛顿定律，列方程： Tsin 0=mo'r=mo'lsin 0 Tcose=me 由转速可求出角速度 0=20m 求出拉力 T=mo'l =4n'n'ml 9.8 cos9=4nn7=4rX050.497 0=6013 可以看出，物体的转速愈大，日也愈大，而与重物的质量m无关。 例题24计算一小球在水中竖直沉降的速度。己知小球的质量为m,水对小球的浮力 为B,水对小球的粘性力为R=Kv,式中K是和水的粘性、小球的半径有关的 一个常量

12 12 解：(1)以小球为研究对象，当小车沿水平方向作匀加速运动时，分析受力： 在竖直方向小球加速度为零，水平方向的加速度为 a。建立图示坐标系： 利用牛顿第二定律，列方程： x 方向 y 方向： 解方程组，得到： (2)以小球为研究对象，当小车沿斜面作匀加速运动时，分析受力： 小球的加速度沿斜面向上，垂直于斜面处于平衡状态，建立图示坐标系，重力与轴的夹 角为 。 利用牛顿第二定律，列方程： 求解上面方程组，得到： 讨论：如果 =0，a1=a2，则实际上是小车在水平方向作匀加速直线运动；如果 =0，加 速度为零，悬线保持在竖直方向。 例题 2-3 一重物 m 用绳悬起，绳的另一端系在天花板上，绳长 l=0.5m，重物经推动后， 在一水平面内作匀速率圆周运动，转速 n=1r/s。这种装置叫做圆锥摆。求这时绳和竖直方向 所成的角度。 解：绳以小球为研究对象，对其进行受力分析： 小球的运动情况，竖直方向平衡，水平方向作匀速圆周运动，建立坐标系如图： 拉力的沿两轴进行分解，竖直方向的分量与重力平衡，水平方向的分力提供向心力。利 用牛顿定律，列方程： 由转速可求出角速度： 求出拉力 可以看出，物体的转速 n 愈大， 也愈大，而与重物的质量 m 无关。 例题 2-4 计算一小球在水中竖直沉降的速度。已知小球的质量为 m，水对小球的浮力 为 B，水对小球的粘性力为 R=-Kv，式中 K 是和水的粘性、小球的半径有关的一个常量 1 1 T sin  = ma T1 cos −mg = 0 tg , 1 g a  = g a1  = arc tg 2 2 T sin( +)−mgsin = ma T2 cos( +)−mgcos = 0  a2 y x o g  m m T2      2 2 2 2 2 T = m (g sin + a ) + g cos 2 2 2 2 2 = m 2ga sin  + a + g     cos sin tg( ) 2 g g + a +  =     − +  = cos sin arc tg 2 g g a T m r 2 sin  =   sin  2 = m l T cos = mg  = 2n T m l 2 =  n ml 2 2 = 4 n l g 2 2 4 cos   = 0.497 4 0.5 9.8 2 =  =  = 60 13   g  m o x y g  m T  T sin  T cos m   T  2 1 2 T1 = m g + a