电子科技大学：《现代网络理论与综合 Theory and Synthesize of Electric Network》课程教学资源（课件讲稿）第6讲 网络函数拓扑法

第6讲网络函数拓扑法 对应教材3-4节

第6讲 网络函数拓扑法 对应教材3-4节

利用拓扑方法求网络函数 1 2 线性无源网络 节点方程：Ynun=Im 11y12 41 y21y2 2·y2n u2 2 二 in

n n n Y u  I 线性无源网络 利用拓扑方法求网络函数 节点方程： i2 u1 u2 i1                                            n n nn n n n n i i i u u u y y y y y y y y y . . . . . . . . . 2 1 2 1 1 2 21 22 2 11 12 1

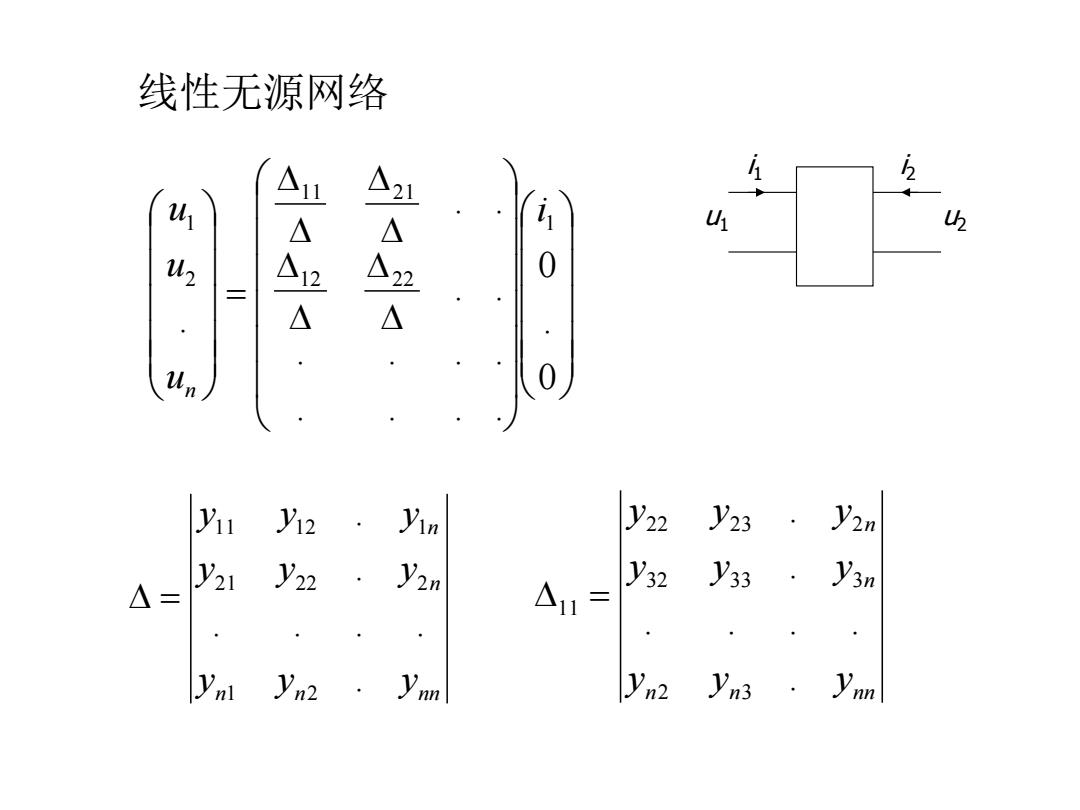
线性无源网络 △21 41 1W2 0 yu y2·yn y22 y23·y2n y21 y22·y2m y32 y33· y3n △= △1= 2·ym yn2 yn3 ·ym

线性无源网络 i2 u1 u2 i1          0.0 . . . . . . . . . . . . . 1 12 22 11 21 21 i uuu n n n nnnn y y y y y y y y y . . . . . .. 1 2 21 22 2 11 12 1   n n nnnn y y y y y y y y y . . . . . .. 2 3 32 33 3 22 23 2 11 

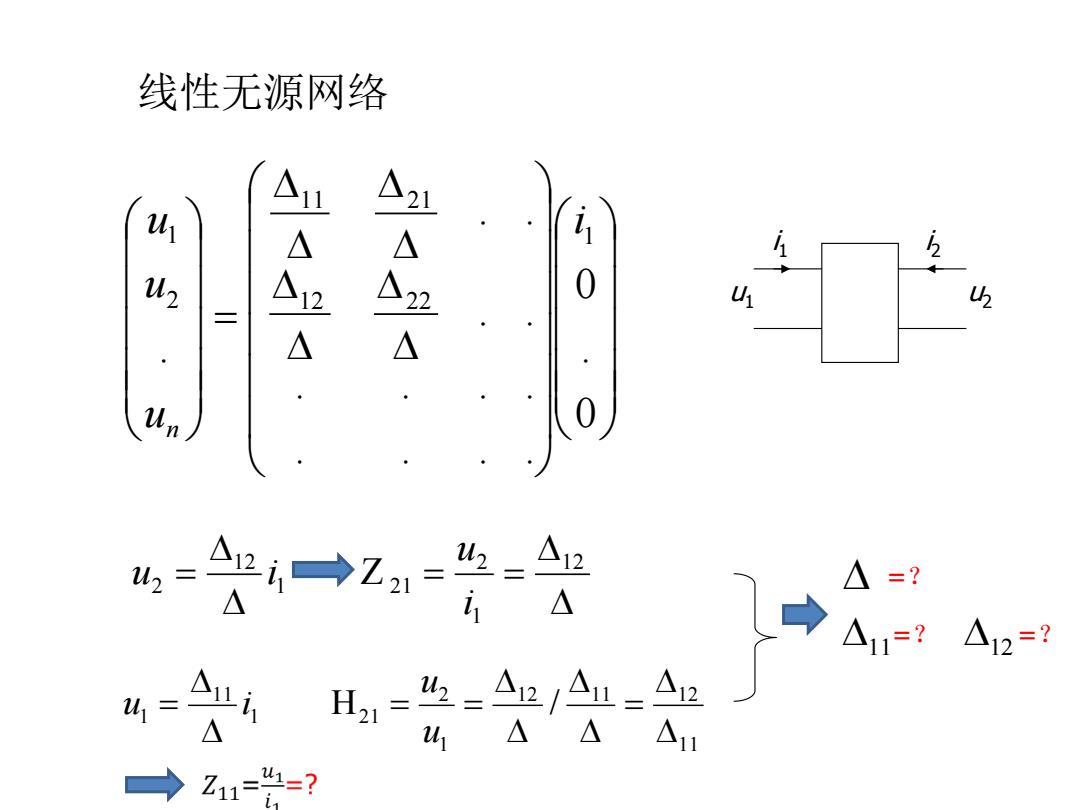
线性无源网络 41 2 42 0 U △ Un 42= 12 △=？ i A →A?An-8 △ △△△ → Z11= 1=?

线性无源网络        12 1 2 1 21 12 2 Z i u u i i2 u1 u2 i1                                                      0 . 0 . . . . . . . . . . . . . 1 12 22 11 21 2 1 i u u u n 11 12 11 12 1 2 1 21 11 1 H /             u u u i  11 12   =？ =？ =？

线性无源网络 已知：△=detY, Y =AY,A →△=dety.=det Ar A' 定理3-1：比内一柯西定理 det D=∑CD, 其中，C、D分别为p×q和q×p的矩阵，且p≤q。 C;和D;分别为矩阵C和D的第j个大子式。 什么是“大子式”？

线性无源网络   j det CD C j D j T n b T n b n Y AY A Y AY A Y det det det       定理3-1：比内—柯西定理 已知： 什么是“大子式”？