
The Platonic Polydedra:f=2+e-v Tetrahedron Cube Octahedron Dodecahedron Icosahedron .Triangles.The interior angle of an equilateral triangle is 60 degrees. Thus on a regular polyhedron,only 3,4,or 5 triangles can meet a vertex If there were more than 6 their angles would add up to at least 360 degrees which they can't.Consider the possibilities: .3 triangles meet at each vertex.This gives rise to a Tetrahedron. 3AECE MA .4 triangles meet at each vertex.This gives rise to an Octahedron. AEOHAPA SMAEP .5 triangles meet at each vertex.This gives rise to an Icosahedron 20 DDR .Squares.Since the interior angle of a square is 90 degrees,at most three squares can meet at a vertex.This is indeed possible and it gives rise to a hexahedron or cube LEONHARD EULER 1707-1783 .Pentagons.As in the case of cubes,the only possibility is that three pentagons meet at a vertex.This gives rise to a Dodecahedron. .Hexagons or regular polygons with more than six sides cannot form the faces of a regular polyhedron since their interior angles are at least 120 degrees. 26
Tetrahedron Cube Octahedron Dodecahedron Icosahedron •Triangles. The interior angle of an equilateral triangle is 60 degrees. Thus on a regular polyhedron, only 3, 4, or 5 triangles can meet a vertex. If there were more than 6 their angles would add up to at least 360 degrees which they can't. Consider the possibilities: •3 triangles meet at each vertex. This gives rise to a Tetrahedron. •4 triangles meet at each vertex. This gives rise to an Octahedron. •5 triangles meet at each vertex. This gives rise to an Icosahedron •Squares. Since the interior angle of a square is 90 degrees, at most three squares can meet at a vertex. This is indeed possible and it gives rise to a hexahedron or cube. •Pentagons. As in the case of cubes, the only possibility is that three pentagons meet at a vertex. This gives rise to a Dodecahedron. •Hexagons or regular polygons with more than six sides cannot form the faces of a regular polyhedron since their interior angles are at least 120 degrees. The Platonic Polydedra: f=2+e-v 26

重要知识点: Euler's theorem for fullerenes:F-E+V=2 F-faces,E-edges,V-vertices (1)E=3V/2→F+V-2=3V/2→F=VI2+2 (2)F=p+h=V/2+2 (3)3V=5p+6h (where p and h are number of pentagonal and hexagonal faces,respectively) (4)Let(2)x6-(3)→p=12 →h=V/2+2-p=V/2-10 V=2(10+h) C20,C24,C28,.,C60,C70,C2(10+h) 27
(1) E = 3V/2 F+V-2=3V/2 F=V/2+2 (2) F = p + h =V/2+2 (3) 3V = 5p + 6h (4) Let (2)x6-(3) р=12 h=V/2+2-p = V/2 - 10 (where p and h are number of pentagonal and hexagonal faces, respectively) Euler’s theorem for fullerenes: F – E + V = 2 F - faces, E - edges, V –vertices 27 С20, С24, С28, ., С60, С70, С2(10+h) . V = 2(10 +h) 重要知识点:
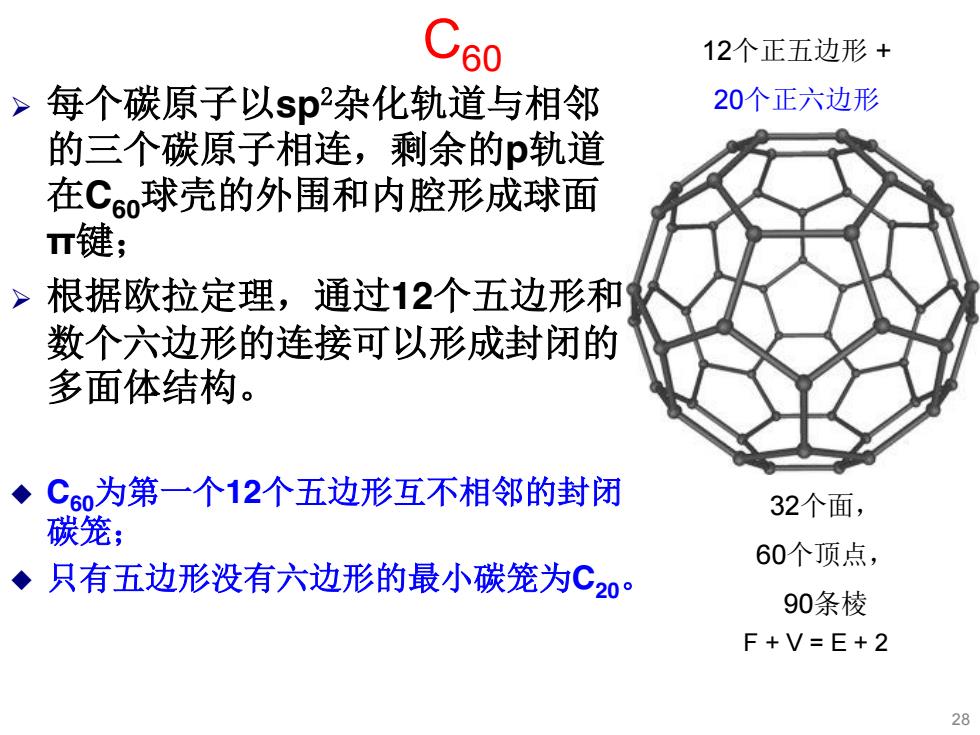
C60 12个正五边形+ > 每个碳原子以sp杂化轨道与相邻 20个正六边形 的三个碳原子相连,剩余的p轨道 在C60球壳的外围和内腔形成球面 T键; >根据欧拉定理,通过12个五边形和 数个六边形的连接可以形成封闭的 多面体结构。 C6为第一个12个五边形互不相邻的封闭 32个面, 碳笼; 60个顶点, ◆只有五边形没有六边形的最小碳笼为C20。 90条棱 F+V=E+2 28
¾ 每个碳原子以sp2杂化轨道与相邻 的三个碳原子相连,剩余的p轨道 在C60球壳的外围和内腔形成球面 π键; ¾ 根据欧拉定理,通过12个五边形和 数个六边形的连接可以形成封闭的 多面体结构。 C60为第一个12个五边形互不相邻的封闭 碳笼; 只有五边形没有六边形的最小碳笼为C20。 F + V = E + 2 C60 32个面, 60个顶点, 90条棱 12个正五边形 + 20个正六边形 28

Science NOW UP T0 THE MINUTE NEWS FRON SCIENCE Fullerene Discoverers Win Chemistry Nobel by Science News Staff on 9 October 1996.8:00 PM The Nobel Prize in chemistry was awarded today to two Americans and one British researcher for their discovery of fullerenes,a new class of all-carbon molecules shaped like hollow balls. The researchers,Richard E.Smalley and Robert F.Curl Jr.of Rice University in Houston,and Harold W.Kroto of the University of Sussex in Brighton,United Kingdom,made their discovery in 1985 in Smalley's lab at Rice while working together to study how carbon atoms cluster. "The award is richly deserved,"says Robert Haddon,a fullerene chemist at Lucent Technologies'Bell Labs in Murray Hill,New Jersey."It led to a totally new field of chemistry."Today,fullerenes-which are popularly known as buckyballs-are being investigated for everything from new superconductors and three-dimensional polymers,to catalysts and optical materials,although they have yet to spawn any commercial applications. Before the group's discovery,crystalline carbon was thought to adopt only a handful of different molecular architectures,including those found in diamond and graphite. But the researchers discovered that sheets of carbon atoms arranged in a pattern of hexagons and pentagons can curl up and ultimately close to form hollow cages.And because the number of atoms in the cage can vary,an almost infinite number of fullerene shapes may exist. 29
The Nobel Prize in chemistry was awarded today to two Americans and one British researcher for their discovery of fullerenes, a new class of all-carbon molecules shaped like hollow balls. The researchers, Richard E. Smalley and Robert F. Curl Jr. of Rice University in Houston, and Harold W. Kroto of the University of Sussex in Brighton, United Kingdom, made their discovery in 1985 in Smalley's lab at Rice while working together to study how carbon atoms cluster. "The award is richly deserved," says Robert Haddon, a fullerene chemist at Lucent Technologies' Bell Labs in Murray Hill, New Jersey. "It led to a totally new field of chemistry." Today, fullerenes-which are popularly known as buckyballs-are being investigated for everything from new superconductors and three-dimensional polymers, to catalysts and optical materials, although they have yet to spawn any commercial applications. Before the group's discovery, crystalline carbon was thought to adopt only a handful of different molecular architectures, including those found in diamond and graphite. But the researchers discovered that sheets of carbon atoms arranged in a pattern of hexagons and pentagons can curl up and ultimately close to form hollow cages. And because the number of atoms in the cage can vary, an almost infinite number of fullerene shapes may exist. Fullerene Discoverers Win Chemistry Nobel 29
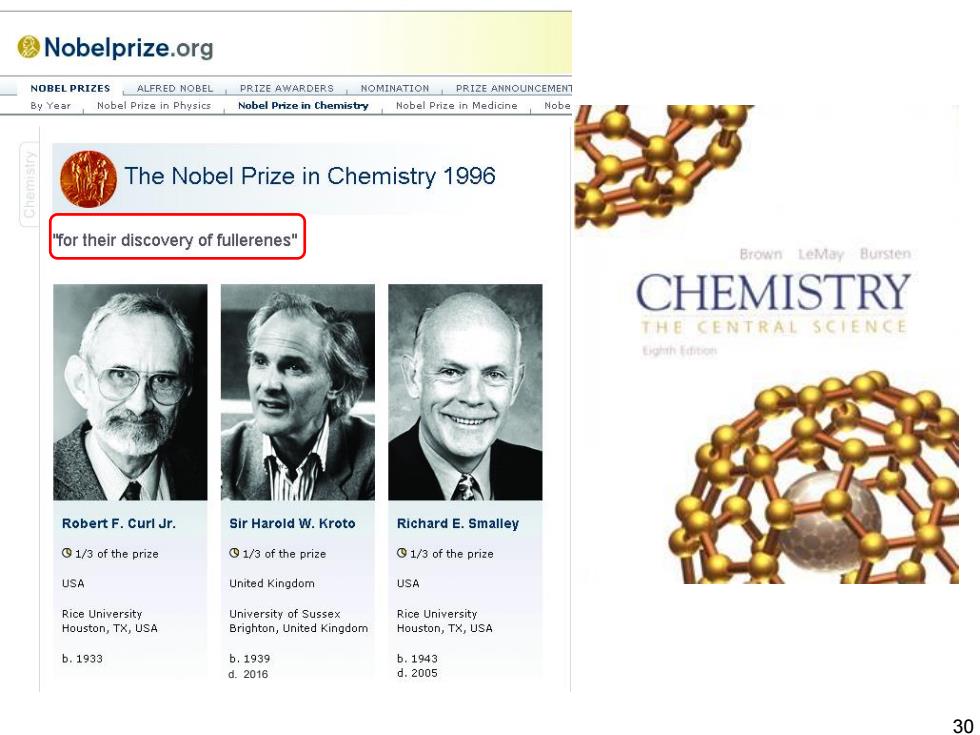
®Nobelprize.org NOBEL PRIZES ALFRED NOBEL PRIZE AWARDERS NOMINATION PRIZE ANNOUNCEMENT By Year Nobel Prize in Physics Nobel Prize in Chemistry Nobel Prize in Medicine Nobe The Nobel Prize in Chemistry 1996 for their discovery of fullerenes' Brown LeMay Bursten CHEMISTRY THE CENTRAL SCIENCE Robert F.Curl Jr Sir Harold W.Kroto Richard E.Smalley 1/3 of the prize 1/3 of the prize ©1/3 of the prize USA United Kingdom USA Rice University University of Sussex Rice University Houston,TX,USA Brighton,United Kingdom Houston,TX,USA b,1933 b,1939 b.1943 d.2016 d.2005 30
30 d. 2016