电子科技大学：《导波场论 Field Theory of Guided Waves》课程教学资源（课件讲稿）第二章 规则波导理论（1/5）

2.1柱形波导系统中扬的求解方法 口目标：柱形波导系统中场的求解方法纵向场法 口内容：推导纵向场与横向场之间的关系 ▣作用：简化问题，减少变量 口思路：从麦克斯韦方程组，波动方程，出发 口条件：波导条件，理想均匀条件，无源条件，无限条件 导波场论 11

2.1柱形波导系统中场的求解方法 p 目标：柱形波导系统中场的求解方法----纵向场法 p 内容： 推导纵向场与横向场之间的关系 p 作用：简化问题，减少变量 p 思路：从麦克斯韦方程组，波动方程，出发 p 条件：波导条件，理想均匀条件，无源条件，无限条件 导波场论 11

2.1柱形波导系统中场的求解方法 口由于无源系统，所以 口齐次亥姆赫兹 麦克斯韦方程为： 方程为 7×H=j0sE V×E=-joH 72E+k2E=0 7.E=0 7五+k2ǖ=0 7.i=0 口其场分量形式可以写为 VE,+k2E.=0,V2H,+k2H.=0 口横向场方程 V2E.+k2E,=0,V2H,+k2H,=0 V2E.+k2E.=0,72H,+k2H.=0 口纵向场方程 导波场论 12

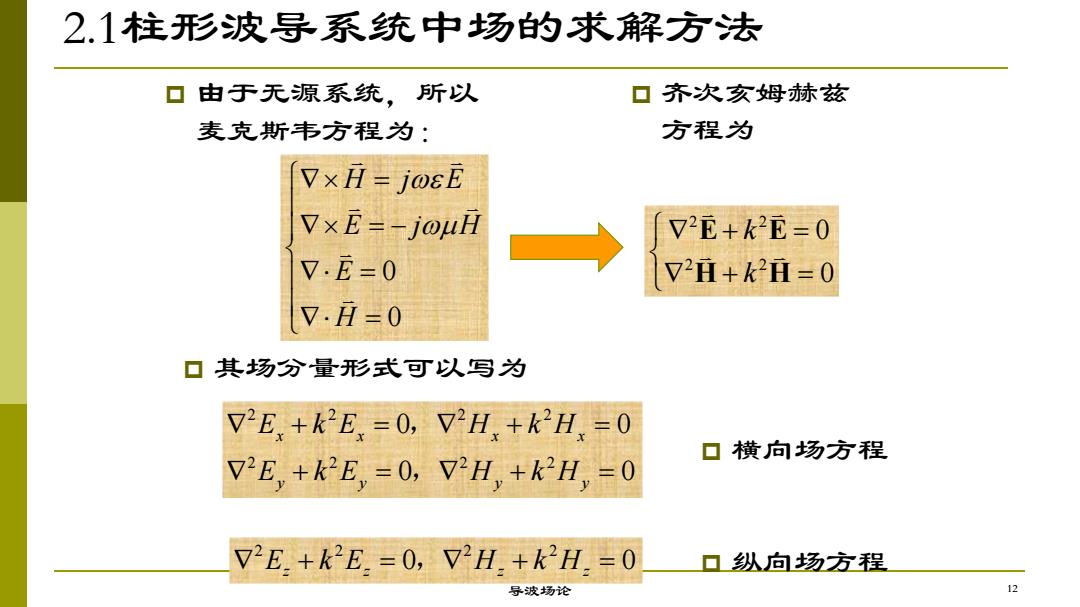
2.1柱形波导系统中场的求解方法 导波场论 p 其场分量形式可以写为 p 横向场方程 p 纵向场方程 p 由于无源系统，所以 麦克斯韦方程为： p 齐次亥姆赫兹 方程为 0 0 H j E E j H E H                   2 2 2 2 0 0 k k         E E H H     2 2 2 2 2 2 2 2 0 0 0 0 x x x x y y y y E k E H k H E k E H k H             ， ， 2 2 2 2 0 0 E z z z z   k E  ， H  k H  12

2.1柱形波导系统中扬的求解方法 口为什么亥姆赫兹方程可以写为横向方程和纵向方程？ 7E+k2E=0 V2(eE,+e E,+e.E.)+k2(eE,+e,E+e.E.)=O 72E.+k2E=0 r2 0z2 (e,E,+e,E,+e.E. VE,+k2E,=0 +k2(e,E,+e,E,+e.E)=0 VE.+k2E.=0 导波场论

2.1柱形波导系统中场的求解方法 p 为什么亥姆赫兹方程可以写为横向方程和纵向方程？ 导波场论 2 2  E k E  0       2 2 0 x x y y z z x x y y z z  e E  e E  e E  k e E  e E  e E            2 2 2 2 2 2 2 0 x x y y z z x x y y z z e E e E e E x y z k e E e E e E                           2 2 2 2 2 2 0 0 0 x x y y z z E k E E k E E k E          13

2.1柱形波导系统中场的求解方法 口被导电滋波的解结构：由于电兹波沿轴向（亿方向）传输，故 E(x,y,)=E(x,y)e 口待求的分量包括 H(x,y,z)=H(x,y)e E,(x,y,=)=E,(x,y)e H,(x,y,=)=H,(x,y)e E,(x,y,=)=E,(x,y)ei H,(x,y,2)=H,(x,y)e E.(x,y,2)=E.(x,y)e H.(x,y,z)=H.(x,y)e 口其中 E(x,y,z人E,(x,y,z)H(x,y,人H(x,y,z) 口横向分量 E.(x,y,)H.(x,y,2) 口纵向分量 导波场论 14

2.1柱形波导系统中场的求解方法 p 被导电磁波的解结构：由于电磁波沿轴向(z方向)传输，故 p 待求的分量包括 p 其中 导波场论 p 横向分量 p 纵向分量 ( , , ) ( , )e ( , , ) ( , )e z z x y z x y x y z x y           E E H H ( , , ) ( , )e ( , , ) ( , )e ( , , ) ( , )e z x x z y y z z z E x y z E x y E x y z E x y E x y z E x y          ( , , ) ( , )e ( , , ) ( , )e ( , , ) ( , )e z x x z y y z z z H x y z H x y H x y z H x y H x y z H x y          ( , , ) ( , , ) ( , , ) ( , , ) Ex y x y x y z 、E x y z 、H x y z 、H x y z ( , , ) ( , , ) E z z x y z 、H x y z 14

2.1柱形波导系统中场的求解方法 直角坐标系中展开 +yE,=-jouH OE. OE. H V×E=-joui→ax +yE,=joμH H: ay OE OE, =-joμuH H,= (J08 E+Y oy OH 0x a Ox Ex= 1 E 直角坐标系中展开 OH.yH,-joeE, Ox jo H) dy E VxH=josE → OH. E,= 2 H) +yH=-jogE y -j04 8x aH, H, josE. k=y2+k2,k2=o218 Ox ay 导波场论

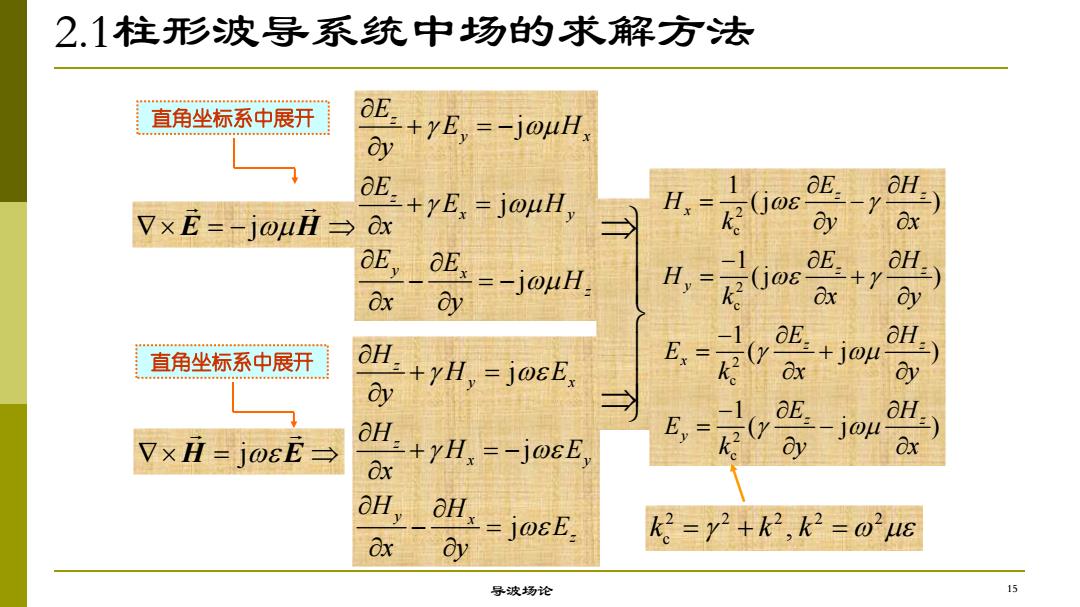
2.1柱形波导系统中场的求解方法 导波场论 直角坐标系中展开 直角坐标系中展开   j    E H   j    H E j j j z y x z x y y x z E E H y E E H x E E H x y                      j j j z y x z x y y x z H H E y H H E x H H E x y                          2 c 2 c 2 c 2 c 1 (j ) 1 (j ) 1 ( j ) 1 ( j ) z z x z z y z z x z z y E H H k y x E H H k x y E H E k x y E H E k y x                                    2 2 2 2 2 c k    k , k   15