
§14-1约束、虚位移和虚功 虚位移与实位移的区别 一个被约束固定曲面上的质点,它的实际微小位移只 是一个,而虚位移在它的约束面上则有任意多个 虚位移与实位移的联系 都是约束所允许的位移 对于定常约束而言一实际微小位移一定是虚位移的
16 一个被约束固定曲面上的质点,它的实际微小位移只 是一个,而虚位移在它的约束面上则有任意多个 dr δr δr δr 虚位移与实位移的区别 §14-1 约束、虚位移和虚功 虚位移与实位移的联系 对于定常约束而言- 实际微小位移一定是虚位移的一个 都是约束所允许的位移

§14-1约束、虚位移和虚功 6如何计算质点系虚位移之间的关系 1)几何法-给出法(虚速度法) 对于定常几何约束质点系,其无限小的实位移是虚位移之一 dr vdt 由上式可知微小实位移标 与速度)同向, 各质点的微小实位移间关系与速度间关系相同 因此,可仿照运动学确定速度方向及其相互关系, 确定各质点的虚位移方向及其相互关系 平移刚体各点虚位移之间的关系? 回忆平移刚体各点的速度之间的关系 δ4=6=6=
17 1)几何法-给出法(虚速度法) 6 如何计算质点系虚位移之间的关系 §14-1 约束、虚位移和虚功 对于定常几何约束质点系,其无限小的实位移是虚位移之一 dr = vdt 由上式可知微小实位移 与速度 同向, 各质点的微小实位移间关系与速度间关系相同 dr v 因此,可仿照运动学确定速度方向及其相互关系, 确定各质点的虚位移方向及其相互关系 平移刚体各点虚位移之间的关系? 回忆平移刚体各点的速度之间的关系 A A r B B r C C r rA = rB = r C =

§14-1约束、虚位移和虚功 6如何计算质点系虚位移之间的关系 1)几何法一-给出法(虚速度法) 定轴转动刚体各点的虚位移之间的关系? 回忆转动刚体各点的速度之间的关系 各点虚位移垂直于点到轴心的线段, 大小与线段长度成正比 DA 平面运动刚体各点的虚位移之间的关系? OB 回忆平面运动刚体各点的速度之间的关系7 速度投影定理? 若找到瞬心,则各点的速度大小与点到瞬心的距 18 离成正比例关系,方位垂直于该线段
18 §14-1 约束、虚位移和虚功 6 如何计算质点系虚位移之间的关系 定轴转动刚体各点的虚位移之间的关系? 各点虚位移垂直于点到轴心的线段, 大小与线段长度成正比 1)几何法-给出法(虚速度法) 回忆转动刚体各点的速度之间的关系 O A A r B r OB OA r r B A = B 平面运动刚体各点的虚位移之间的关系? 回忆平面运动刚体各点的速度之间的关系? 速度投影定理? 若找到瞬心,则各点的速度大小与点到瞬心的距 离成正比例关系,方位垂直于该线段
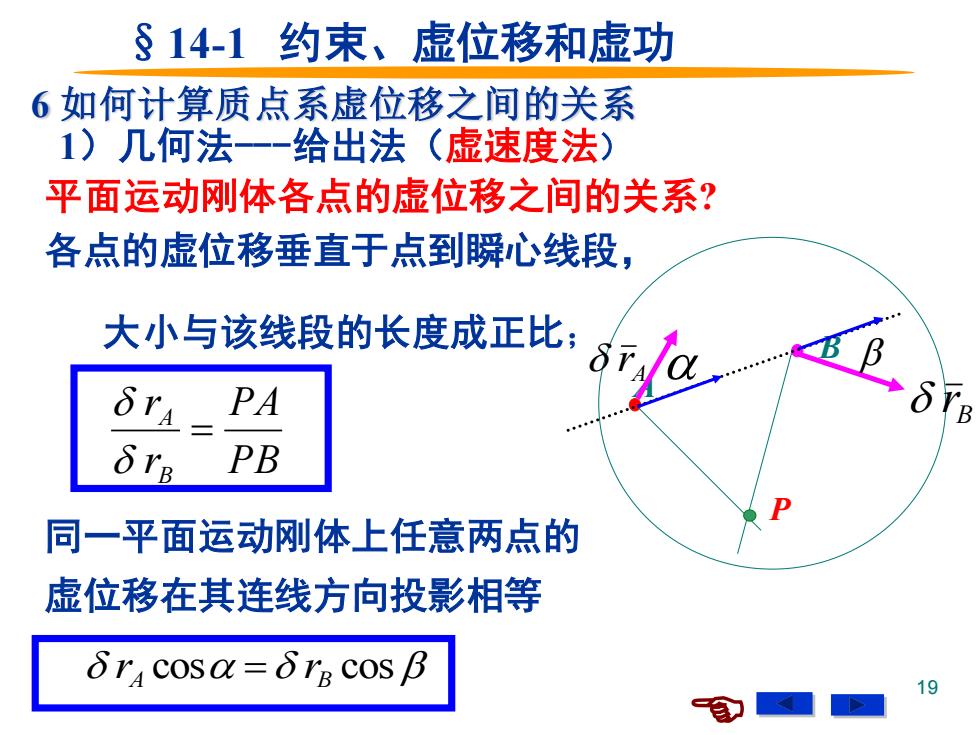
§14-1约束、虚位移和虚功 6如何计算质点系虚位移之间的关系 1)几何法一一给出法(虚速度法) 平面运动刚体各点的虚位移之间的关系? 各点的虚位移垂直于点到瞬心线段, 大小与该线段的长度成正比; 9 PA B PB 同一平面运动刚体上任意两点的 虚位移在其连线方向投影相等 δr cosa=δTE COS B 19
19 §14-1 约束、虚位移和虚功 6 如何计算质点系虚位移之间的关系 平面运动刚体各点的虚位移之间的关系? 1)几何法-给出法(虚速度法) 同一平面运动刚体上任意两点的 虚位移在其连线方向投影相等 各点的虚位移垂直于点到瞬心线段, 大小与该线段的长度成正比; A B A r B r P PB PA r r B A = rA cos = rB cos
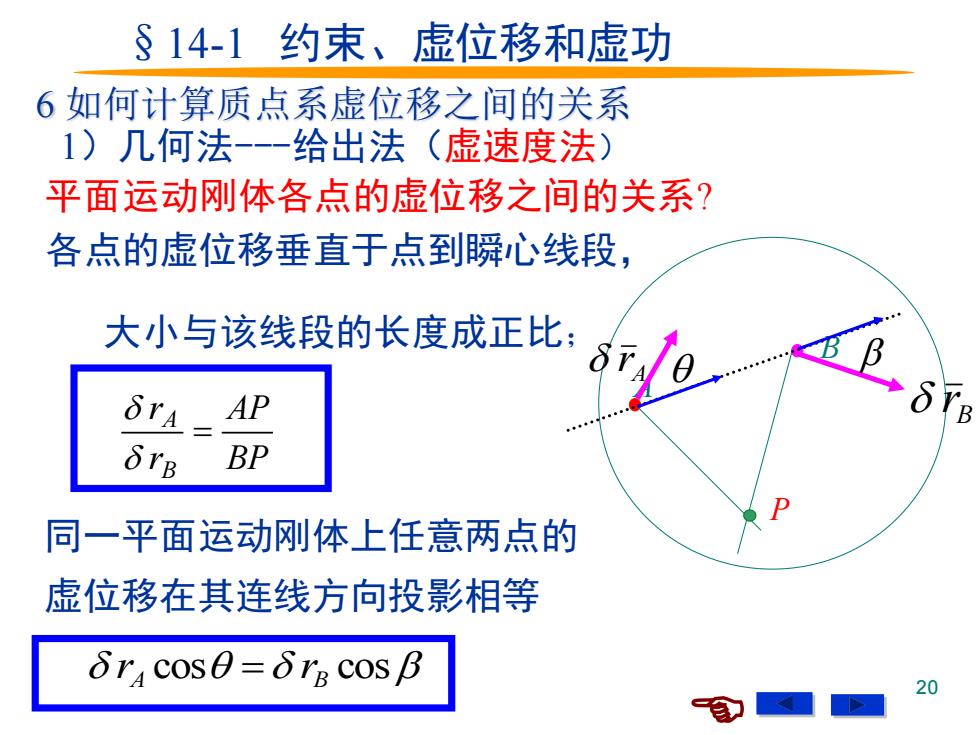
§14-1约束、虚位移和虚功 6如何计算质点系虚位移之间的关系 1)几何法-给出法(虚速度法) 平面运动刚体各点的虚位移之间的关系? 各点的虚位移垂直于点到瞬心线段, 大小与该线段的长度成正比: 8 6r4- AP 6rB BP 同一平面运动刚体上任意两点的 虚位移在其连线方向投影相等 δr4coS0=δTE COS B 20
20 §14-1 约束、虚位移和虚功 6 如何计算质点系虚位移之间的关系 平面运动刚体各点的虚位移之间的关系? 1)几何法-给出法(虚速度法) 同一平面运动刚体上任意两点的 虚位移在其连线方向投影相等 各点的虚位移垂直于点到瞬心线段, 大小与该线段的长度成正比; A B A r B r P BP AP r r B A = rA cos = rB cos