
§14-1约束、虚位移和虚功 例题4半径为R沿直线路面做纯滚动的车轮 y。=R xc=Ro X 例题5一摆长随时间变化的单摆 LL 该单摆的约束方程 X 1。-ut x2+y2=(亿。-ut)2 M(x,y) y
6 §14-1 约束、虚位移和虚功 x o y R c x C c x 例题4 半径为R 沿直线路面做纯滚动的车轮 yc = R x R c = o x y M (x, y) u l ut o − 该单摆的约束方程 2 2 2 x y (l ut) + = o − 例题5一摆长随时间变化的单摆

§14-1约束、虚位移和虚功 二约束的分类1定常约束和非定常约束 定常约束-约束条件不随时间变化 x2+y2=12 非定常约束-约束条件随时间变化 该单摆的约束方程 A(x,y) x2+y2=(L。-ut)2 x 1。-t M(x,y)
7 o x y A(x, y) l §14-1 约束、虚位移和虚功 二 约束的分类 1 定常约束和非定常约束 定常约束-约束条件不随时间变化 M 2 2 2 x + y = l 非定常约束-约束条件随时间变化 o x y M (x, y) u l ut o − 该单摆的约束方程 2 2 2 x y (l ut) + = o −
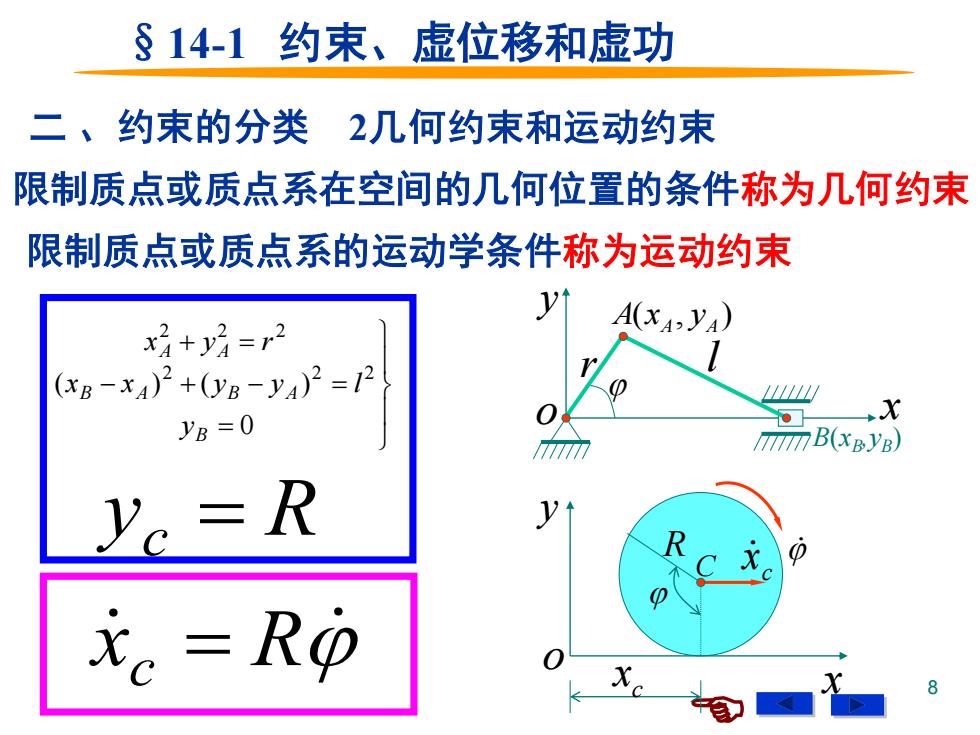
§14-1约束、虚位移和虚功 二、约束的分类2几何约束和运动约束 限制质点或质点系在空间的几何位置的条件称为几何约束 限制质点或质点系的运动学条件称为运动约束 x+=r2 A() (xB-x4)2+(0yB-y4)2=12 yB=0 →X T77B(xByB) y。 -R 12 R x=Ro
8 §14-1 约束、虚位移和虚功 二 、约束的分类 2几何约束和运动约束 限制质点或质点系在空间的几何位置的条件称为几何约束 o ( , ) A A A x y y x r l B(xB ,yB ) = − + − = + = 0 ( ) ( ) 2 2 2 2 2 2 B B A B A A A y x x y y l x y r yc = R 限制质点或质点系的运动学条件称为运动约束 x o y R c x C c x x R c =

§14-1约束、虚位移和虚功 二约束的分类 3其他分类一完整约束和非完整约束 若约束方程的一般形式为 f, =0 (j=1,2,) 式中n为系统中质点的个数,s为约束方程的数目 显含坐标对时间的导数的约束方程是微分方程 如果这方程不可积分成有限形式,则相应的约束称为非完 整约束 如果这方程可积分成有限形式,则相应的约束称为完整约 束 xc=Ro xc=Ro
9 §14-1 约束、虚位移和虚功 二 约束的分类 3 其他分类—完整约束和非完整约束 若约束方程的一般形式为 ( , , ;.; , , ; , , ,.; 1 1 1 1 1 1 f x y z x y z x y z j n n n x , y , z ;t) = 0 n n n ( j =1, 2,.,s) 式中n为系统中质点的个数,s为约束方程的数目 如果这方程不可积分成有限形式,则相应的约束称为非完 整约束 显含坐标对时间的导数的约束方程是微分方程 如果这方程可积分成有限形式,则相应的约束称为完整约 束 x R c = xc = R

§14-1约束、虚位移和虚功 3其他分类一完整约束和非完整约束 显含坐标对时间的导数的约束方程是微分方程 如果这方程不可积分成有限形式,则相应的约束称为非完 整约束 B 10
10 §14-1 约束、虚位移和虚功 3 其他分类—完整约束和非完整约束 如果这方程不可积分成有限形式,则相应的约束称为非完 整约束 显含坐标对时间的导数的约束方程是微分方程 A B C