
d5≥82”号为不可逆过程 号为可逆过程 d5≥0一号为自发过程 =”号为处于平衡状态 因为隔离体系中一且发生一个不可逆过程,则一定是自发过程。有时把与体系密切相 关的环境也包括在一起,用来判断过程的自发性,即: △S。=△S(体系)+△S(环境)20 >”号为自发过程 “=”号为可逆过程 世界直有末日吗? 熵增原理 dS隔≥0或4S隔≥0 自发 平衡 热寂论:字宙是隔高系统,其过程总是自发的,因此痛总是增加,朝无序发展,最终达到 极限一热力学绝对平衡,即高度无序,温度完全一致,任何事物都不会变了! 这不是很好吗?不再受热、挨冻,人人公平!这就修了1世界不会变了,值得可爱吗? 你们都不要太高兴或太悲哀1谁说宇 宙是隔高系统 热力学定律是在有限的空 间中总结出的规律,应用到无限的空间中时,请问是否保证成立? 3.6热力学基本方程与TS图 一、热力学基本方程一热力学第一和第二定律的联合公式 系统在可逆过程中所吸收的热为δQR 此过程中的熵变为 a5-8g 根据热力学第一定律 dU=60+6W dU =TdS-pdv 这是热力学第一与第二定律的联合公式,适用于组成恒定、不作非膨胀功的封闭体系。 注意: 虽然用到了80e=TdS 的公式,但适用于任何可逆或不可逆过程,因为式中的物理量 皆是状态函数,其变化值仅决定于始、终态。但只有在可逆过程中TS才代表δQ -pd业才代表δW Tds=dU pdv ds=7d0+号dr S=U,) 比较(1)(2)得: ()片度T() 6
6 “>” 号为不可逆过程 “=” 号为可逆过程 “>” 号为自发过程 “=” 号为处于平衡状态 因为隔离体系中一旦发生一个不可逆过程,则一定是自发过程。有时把与体系密切相 关的环境也包括在一起,用来判断过程的自发性,即: “>” 号为自发过程 “=” 号为可逆过程 世界真有末日吗? 熵增原理: dS 隔 ≥ 0 或 ΔS 隔 ≥ 0 自发 平衡 热寂论: 宇宙是隔离系统,其过程总是自发的,因此熵总是增加,朝无序发展,最终达到 极限——热力学绝对平衡,即高度无序,温度完全一致,任何事物都不会变了! 这不是很好吗?不再受热、挨冻,人人公平!这就惨了!世界不会变了,值得可爱吗? 你们都不要太高兴或太悲哀!谁说宇宙是隔离系统? 热力学定律是在有限的空间中总结出的规律,应用到无限的空间中时,请问是否保证成立? 3.6 热力学基本方程与 T-S 图 一、热力学基本方程——热力学第一和第二定律的联合公式 系统在可逆过程中所吸收的热为 QR 此过程中的熵变为 根据热力学第一定律 dU =Q +W 这是热力学第一与第二定律的联合公式,适用于组成恒定、不作非膨胀功的封闭体系。 注 意: 虽然用到了 的公式,但适用于任何可逆或不可逆过程,因为式中的物理量 皆是状态函数,其变化值仅决定于始、终态。但只有在可逆过程中 才代表 , 才代表 。 (1) S=S(U,V) (2) 比较(1)(2)得: 或 d Q T S R = d Q S T iso d 0 S iso = + S S S ( ( 0 体系) 环境) QR dS T = d d d U T S p V = − T Sd QR − p Vd We T S U p V d d d = + 1 d d d P S U V T T = + ( ) ( ) V U S S dS dU dV U V = + 1 V S U T = V U T S =
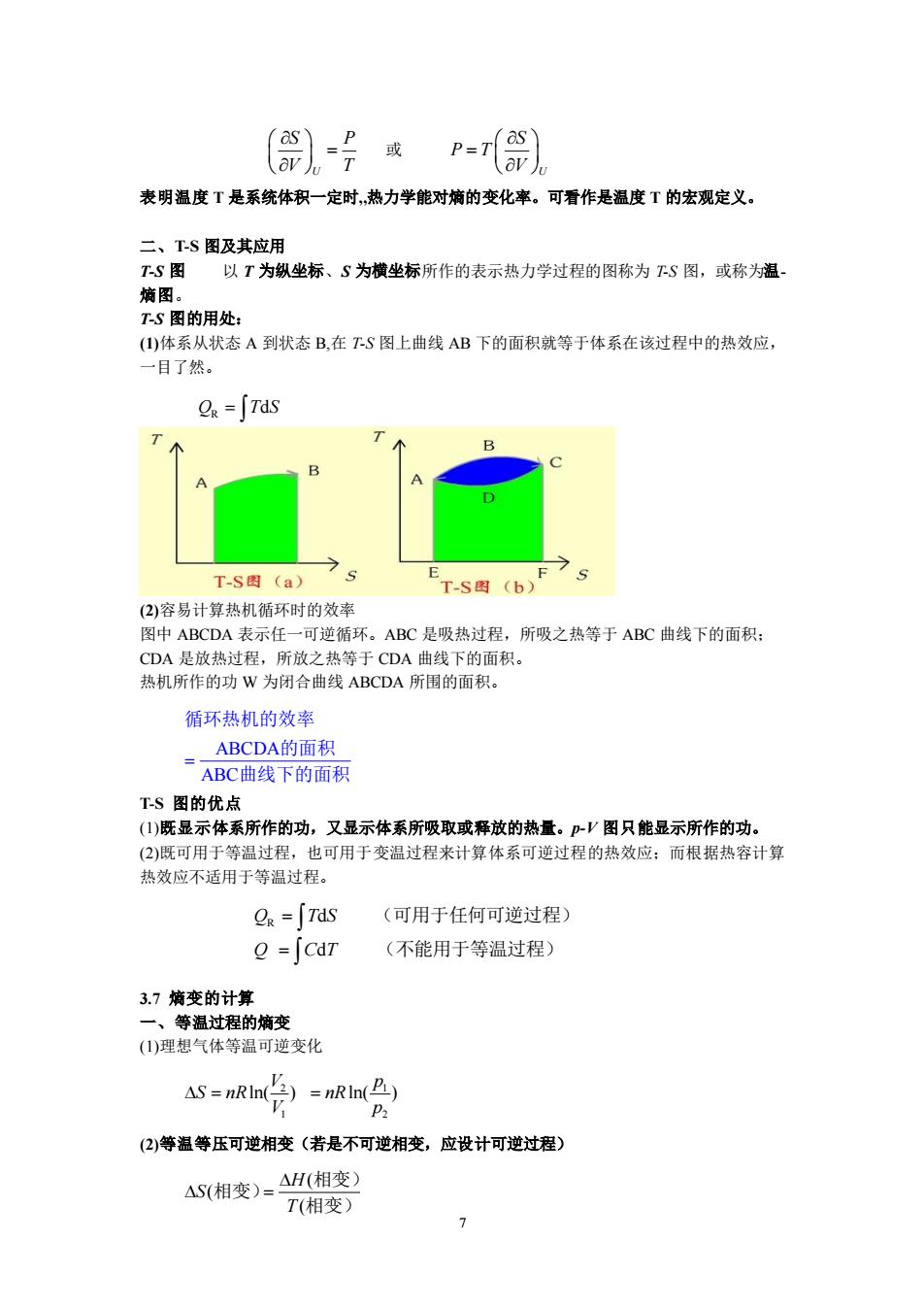
表明温度T是系统体积一定时,热力学能对熵的变化率。可看作是温度T的宏观定义。 二、TS图及其应用 T灯图 以T为纵坐标、S为横坐标所作的表示热力学过程的图称为下S图,或称为温 下S图的用处 ()体系从状态A到状态B,在TS图上曲线AB下的面积就等于体系在该过程中的热效应, 一目了然。 g=∫Tds 75 7 T.S图(a) T-S图(b) (2)容易计算热机循环时的效率 图中ABCDA表示任一可逆循环。ABC是吸热过程,所吸之热等于ABC曲线下的面积: CDA是放热过程,所放之热等于CDA曲线下的面积。 热机所作的功W为闭合曲线ABCDA所围的面积。 循环热机的效率 ABCDA的面积 ABC曲线下的面积 TS图的优点 ()既显示体系所作的功,又显示体系所吸取或释放的热量。p-V图只能显示所作的功, (2)既可用于等温过程,也可用于变温过程来计算体系可逆过程的热效应:而根据热容计算 热效应不适用于等温过程。 g=∫Tds (可用于任何可逆过程)》 2=[caT (不能用于等温过程) 3.7摘变的计算 一、等温过程的嫡变 ()理想气体等温可逆变化 AS=nRin=nRnA (2)等温等压可逆相变(若是不可逆相变,应设计可逆过程) AS(相变)=4H(相变) T(相变)
7 或 表明温度 T 是系统体积一定时,热力学能对熵的变化率。可看作是温度 T 的宏观定义。 二、T-S 图及其应用 T-S 图 以 T 为纵坐标、S 为横坐标所作的表示热力学过程的图称为 T-S 图,或称为温- 熵图。 T-S 图的用处: (1)体系从状态 A 到状态 B,在 T-S 图上曲线 AB 下的面积就等于体系在该过程中的热效应, 一目了然。 (2)容易计算热机循环时的效率 图中 ABCDA 表示任一可逆循环。ABC 是吸热过程,所吸之热等于 ABC 曲线下的面积; CDA 是放热过程,所放之热等于 CDA 曲线下的面积。 热机所作的功 W 为闭合曲线 ABCDA 所围的面积。 T-S 图的优点 (1)既显示体系所作的功,又显示体系所吸取或释放的热量。p-V 图只能显示所作的功。 (2)既可用于等温过程,也可用于变温过程来计算体系可逆过程的热效应;而根据热容计算 热效应不适用于等温过程。 3.7 熵变的计算 一、等温过程的熵变 (1)理想气体等温可逆变化 (2)等温等压可逆相变(若是不可逆相变,应设计可逆过程) U S P V T = U S P T V = R Q T S = d ABCDA ABC = 循环热机的效率 的面积 曲线下的面积 R d d Q T S Q C T = = (可用于任何可逆过程) (不能用于等温过程) 2 1 ln( ) V S nR V = 1 2 ln( ) p nR p = ( ( ( H S T = 相变) 相变) 相变)

(③)理想气体(或理想溶液)的等温等压混合过程,并符合分体积定律,即 △S=-R∑nInxp 例题 例1:1mol理想气体在等温下通过:()可逆膨胀(2)真空膨胀,体积增加到10倍,分别求 其熵变 解:(1)可逆膨胀 △体系)-号。-=nRn 2=nRln10=19.14J-K- △S(隔离)=△S(体系)+△S(环境)=0 (1)为可逆过程。 (2)真空膨胀 熵是状态函数,始终态相同,体系嫡变也相同,所以: △S(体系)=19.14J-K 但环境没有熵变,则: △S(隔离)=△S(体系)=19.14J.K1>0 (2)为不可逆过程 例2:求下述过程熵变。已知H20(1)的汽化热为40.620kJ·mol H,01mol,lp,373.15K)=H,01mol,gp,373.15K) 解: △体系)=(号。=△,=40620:mo=1089J-K.m0r T 373.15K 如果是不可逆相变,可以设计可逆相变求△S值。 例3:在273K时,将一个22.4dm3的盒子用隔板一分为二,一边放0.5molO2(g),另 -边放0.5molN2(g) 解法1: ASo,)=nRn2=05Rn号器 AS(N,)=0.5RIn 22.4 2.2 22Rn2 224 AiS=AS(O2)+AS(N2 )RIn 解法2:AmS=-R∑ng In xa
8 (3)理想气体(或理想溶液)的等温等压混合过程,并符合分体积定律,即 例 题 例 1:1mol 理想气体在等温下通过:(1)可逆膨胀 (2)真空膨胀,体积增加到 10 倍,分别求 其熵变。 解:(1)可逆膨胀 (1)为可逆过程。 (2)真空膨胀 熵是状态函数,始终态相同,体系熵变也相同,所以: 但环境没有熵变,则: (2)为不可逆过程 例 2:求下述过程熵变。已知 H2O(l)的汽化热为 解: 如果是不可逆相变,可以设计可逆相变求 值。 例 3:在 273 K 时,将一个 的盒子用隔板一分为二,一边放 ,另 一边放 解法 1: 解法 2: mix B B B = − S R n x ln B B V x V = max R ( ( ) Q W S T T − = = 体系) 2 1 ln V nR V = 1 nRln10 19.14 J K− = = = + = S S S (隔离) (体系) (环境) 0 1 S 19.14 J K− = (体系) 1 S S 19.14 J K 0 − = = (隔离) (体系) -1 40.620 kJ mol H O(1 mol,l, ,373.15 K) H O(1 mol,g, ,373.15 2 2 p p K) $ $ R Q S T = (体系)( ) vap m b H T = 1 40.620 kJ mol 373.15 K − = 1 1 108.9 J K mol − − = S 3 22.4 dm 0.5 mol O (g) 2 0.5 mol N (g) 2 2 2 1 (O ) ln V S nR V = 22.4 0.5 ln 12.2 = R 2 22.4 (N 0.5 ln 12.2 = S R ) mix 2 2 = + S S S (O ) (N ) 22.4 ln ln 2 12.2 = = R R mix B B B = − S R n x ln