Stress State in an Uncracked Elastic Beam V N.A (c) Shear stress,v Plane y- Coordinates(0,v) 45 Maximum shear stress, Vma× 个120 0 Normal stress,f Plane x Coordinates (f v) IPrincipal compressive Principal tensile stress, stress,fc(max) ft(max) (d) 目 土本工程学院
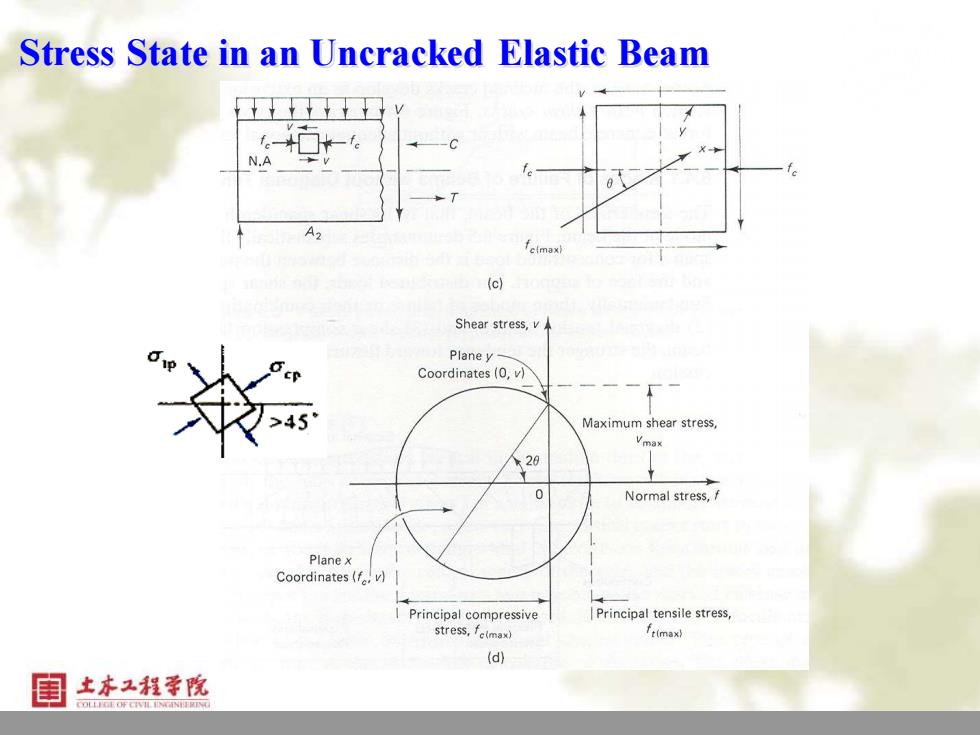
6 Stress State in an Uncracked Elastic Beam

Principal Stresses 中A2 N.A. 中A, a Neutral axis Cross section Shear stress distribution or c(max) +v2 and tan20=2v 土本又程学院
7 Principal Stresses 2 2 or (max) 2 and tan 2 2 2 t t t c t f f v f v f = + =

Trajectory of principal stresses in an Uncracked Elastic Beam Crack type: Vertical cracks Diagonal cracks 闺土本红程幸悦
8 Trajectory of principal stresses in an Uncracked Elastic Beam Crack type: Vertical cracks Diagonal cracks

Shear Stress in an Cracked RC Beam Cracked Beam section Flexural stresses Shear flow Shear stresses Fig.7.3.Shear stresses across an idealized cracked reinforced concrete section. 1 dr 1d(M/jd)dm 1 V V= b。db。 dx dx bjd bjd V ACI:v= bd 土水工程学院
9 Shear Stress in an Cracked RC Beam 1 1 1 ( / ) w w w w dT dM V d M jd v b dx b dx dx b jd b jd = = = = ACI: w V v b d =

Formation of Diagonal cracks Flexure-shear diagonal crack Web-shear diagonal crack Diagonal cracking load Load by principal stress Shrinkage stresses,local weakening of a cross section by transverse reinforcement,redistribution of shear stresses between flexural cracks 土本工程学院
10 Formation of Diagonal cracks Flexure-shear diagonal crack Web-shear diagonal crack Diagonal cracking load ? Load by principal stress Shrinkage stresses, local weakening of a cross section by transverse reinforcement, redistribution of shear stresses between flexural cracks