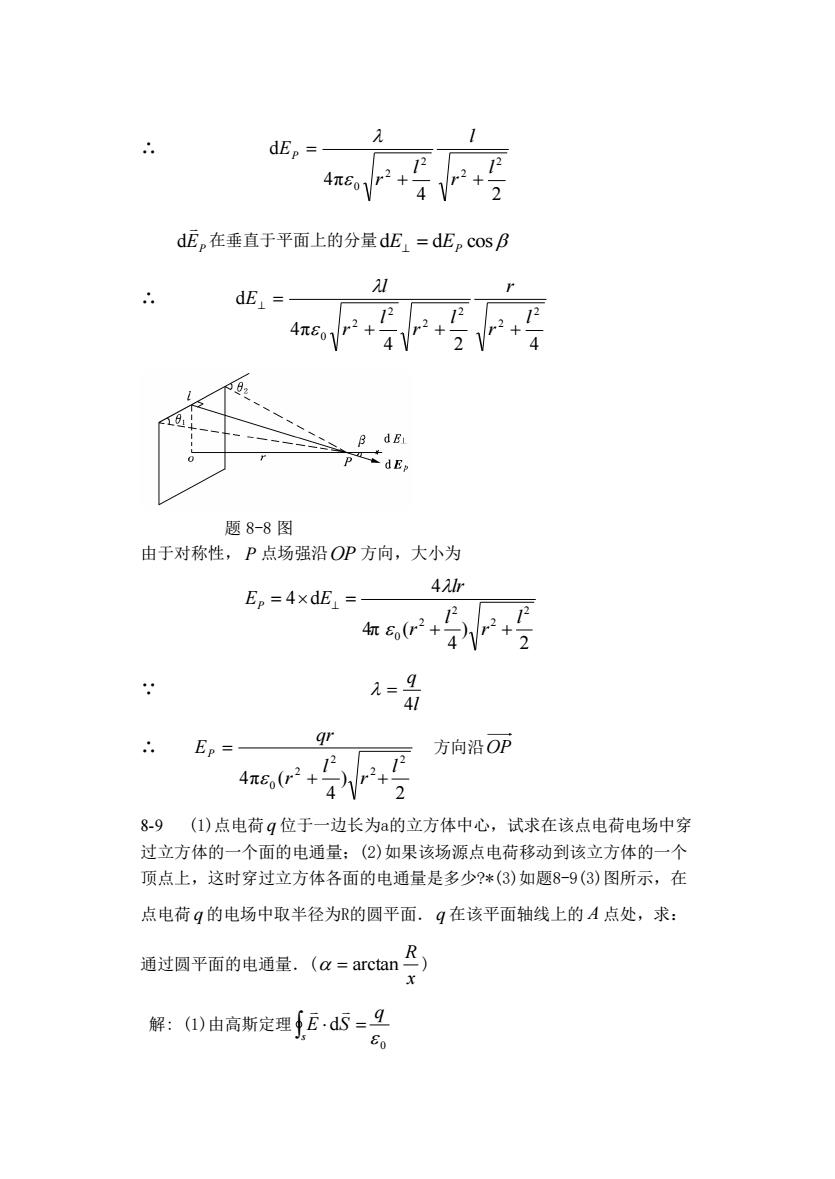
4 dE,在垂直于平面上的分量dE,=dEp cosB dE 题8-8图 由于对称性,P点场强沿OP方向,大小为 Ep=4×dE= 6心写 gr r Ep=- :方向沿OP 8-9(1)点电荷q位于一边长为a的立方体中心,试求在该点电荷电场中穿 过立方体的一个面的电通量:(②)如果该场源点电荷移动到该立方体的一个 项点上,这时穿过立方体各面的电通量是多少?*(3)如题8-9(3)图所示,在 点电荷q的电场中取半径为R的圆平面。q在该平面轴线上的A点处,求: 通过圆平面的电通量.(a=arctan) 解:(1)由高斯定理Ed5=9
∴ 4 2 4π d 2 2 2 2 0 l r l l r EP + + = EP d 在垂直于平面上的分量 dE⊥ = dEP cos ∴ 4 2 4 4π d 2 2 2 2 2 2 0 l r r l r l r l E + + + ⊥ = 题 8-8 图 由于对称性, P 点场强沿 OP 方向,大小为 2 ) 4 4π ( 4 4 d 2 2 2 2 0 l r l r lr EP E + + = ⊥ = ∵ l q 4 = ∴ 2 ) 4 4π ( 2 2 2 2 0 l r l r qr EP + + = 方向沿 OP 8-9 (1)点电荷 q 位于一边长为a的立方体中心,试求在该点电荷电场中穿 过立方体的一个面的电通量;(2)如果该场源点电荷移动到该立方体的一个 顶点上,这时穿过立方体各面的电通量是多少?*(3)如题8-9(3)图所示,在 点电荷 q 的电场中取半径为R的圆平面. q 在该平面轴线上的 A 点处,求: 通过圆平面的电通量.( x R = arctan ) 解: (1)由高斯定理 0 d q E S s =
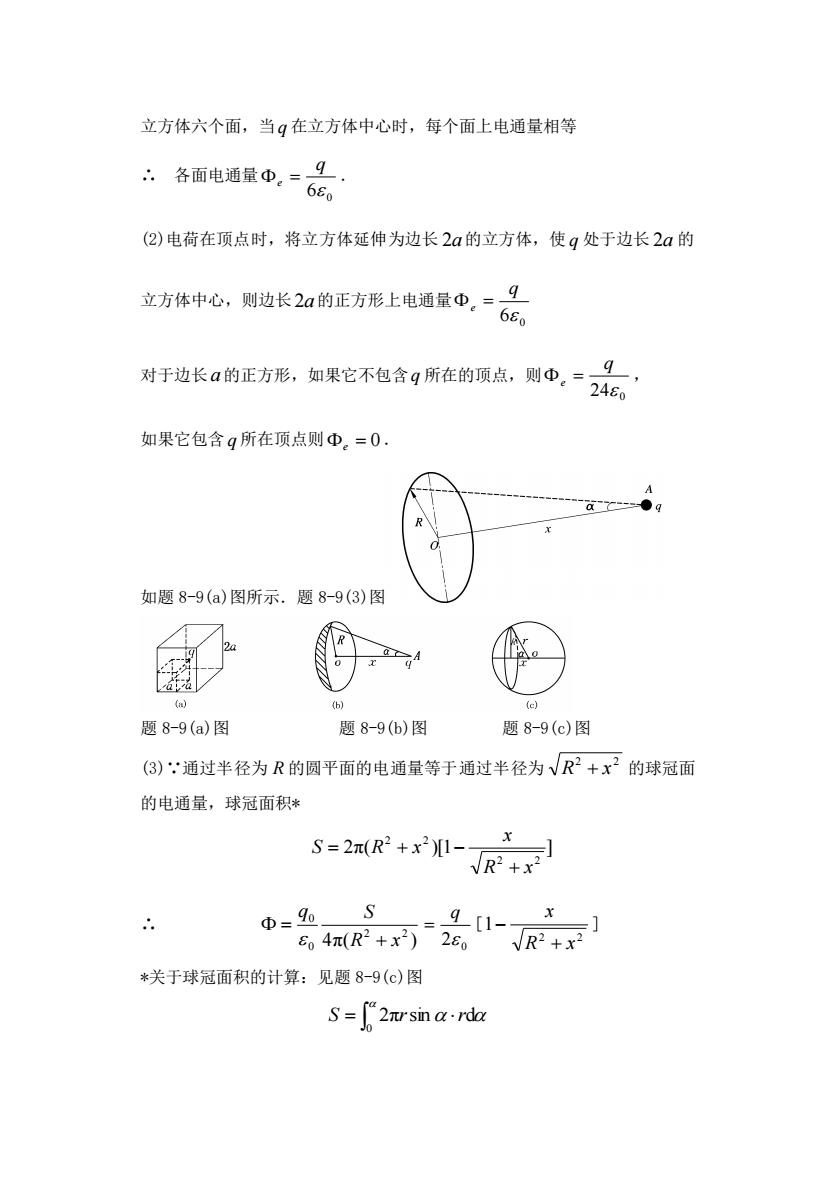
立方体六个面,当g在立方体中心时,每个面上电通量相等 :各面电通量少,一6品 (②)电荷在顶点时,将立方体延伸为边长2a的立方体,使g处于边长2a的 立方体中心,则边长2a的正方形上电通量①。=6G。 9 对于边长a的正方形,如果它不包含g所在的顶点,则心,=是 如果它包含g所在顶点则Φ。=0. 如题8-9(a)图所示.题8-9(3)图 R x (h) 题8-9(a)图 题8-9(6)图 题8-9(c)图 (3):通过半径为R的圆平面的电通量等于通过半径为√R2+x2的球冠面 的电通量,球冠面积* S=2π(R2+x2)1- R Φ=6S g[1- 84π(R2+x)2 VR *关于球冠面积的计算:见题8-9(c)图 S=2rsin a.rda
立方体六个面,当 q 在立方体中心时,每个面上电通量相等 ∴ 各面电通量 6 0 q e = . (2)电荷在顶点时,将立方体延伸为边长 2a 的立方体,使 q 处于边长 2a 的 立方体中心,则边长 2a 的正方形上电通量 6 0 q e = 对于边长 a 的正方形,如果它不包含 q 所在的顶点,则 24 0 q e = , 如果它包含 q 所在顶点则 e = 0. 如题 8-9(a)图所示.题 8-9(3)图 题 8-9(a)图 题 8-9(b)图 题 8-9(c)图 (3)∵通过半径为 R 的圆平面的电通量等于通过半径为 2 2 R + x 的球冠面 的电通量,球冠面积* 2π( )[1 ] 2 2 2 2 R x x S R x + = + − ∴ 4π( ) 2 2 0 0 R x q S + = 2 0 q = [ 2 2 1 R x x + − ] *关于球冠面积的计算:见题 8-9(c)图 = 0 S 2πrsin rd

=2sin a.da =2nr2(1-cosa) 8-10均匀带电球壳内半径6cm,外半径10cm,电荷体密度为2×10-5C·m3 求距球心5cm,8cm,12cm各点的场强. 解:高斯定理fEd5∑9,E4m_9 当r=5cm时,∑g=0,E=0 r=8cm时,∑g=p经-) p- E=48,r2 ≈3.48×101N.C-1,方向沿半径向外 r=12a时∑9=p好味-肉 - .E= ≈4.10×104N.C-沿半径向外 4π6or2 8-11半径为R和R2(R2>R)的两无限长同轴圆柱面,单位长度上分别 带有电量元和-1,试求:(1)r<R:(2)R<r<R:(3)r>R2处各点 的场强。 解:高斯定理fE.d5=∑9 取同轴圆柱形高斯面,侧面积S=2π1 fE.dS=E2xrl 对(1) r<R∑q=0,E=0
= 0 2 2πr sin d 2π (1 cos ) 2 = r − 8-10 均匀带电球壳内半径6cm,外半径10cm,电荷体密度为2× 5 10 − C·m -3 求距球心5cm,8cm ,12cm 各点的场强. 解: 高斯定理 0 d = q E S s , 0 2 4π = q E r 当 r = 5 cm 时, q = 0 , E = 0 r = 8 cm 时, q 3 4π = p 3 (r ) 3 − r内 ∴ ( ) 2 0 3 2 4π 3 4π r r r E − 内 = 4 3.4810 1 N C − , 方向沿半径向外. r = 12 cm 时, 3 4π q = − 3 (r外 r内 3) ∴ ( ) 4 2 0 3 3 4.10 10 4π 3 4π − = r r r E 外 内 1 N C − 沿半径向外. 8-11 半径为 R1 和 R2 ( R2 > R1 )的两无限长同轴圆柱面,单位长度上分别 带有电量 和- ,试求:(1) r < R1 ;(2) R1 < r < R2 ;(3) r > R2 处各点 的场强. 解: 高斯定理 0 d = q E S s 取同轴圆柱形高斯面,侧面积 S = 2πrl 则 E S E rl S d = 2π 对(1) R1 r q = 0,E = 0

R<r<R ∑9=1n E=20 沿径向向外 ⑤ r>R∑q=0 E=0 题8-12图 812两个无限大的平行平面都均匀带电,电荷的面密度分别为σ,和02, 试求空间各处场强。 解:如题8-12图示,两带电平面均匀带电,电荷面密度分别为0,与02, 两面间,E= 26 -(o1-02)n 西*、E=云a+o a面、后=云a+a,折 方:垂直于两平面由o,面指为o,面. 813半径为R的均匀带电球体内的电荷体密度为P,若在球内挖去一块半 径为r<R的小球体,如题8-13图所示.试求:两球心O与O点的场强, 并证明小球空腔内的电场是均匀的。 解:将此带电体看作带正电P的均匀球与带电一P的均匀小球的组合,见 题8-13图(a). (1)+p球在O点产生电场E。=0
(2) 1 R2 R r q = l ∴ r E 2π 0 = 沿径向向外 (3) R2 r q = 0 ∴ E = 0 题 8-12 图 8-12 两个无限大的平行平面都均匀带电,电荷的面密度分别为 1 和 2 , 试求空间各处场强. 解: 如题 8-12 图示,两带电平面均匀带电,电荷面密度分别为 1 与 2 , 两面间, E n ( ) 2 1 1 2 0 = − 1 面外, E n ( ) 2 1 1 2 0 = − + 2 面外, E n ( ) 2 1 1 2 0 = + n :垂直于两平面由 1 面指为 2 面. 8-13 半径为 R 的均匀带电球体内的电荷体密度为 ,若在球内挖去一块半 径为 r < R 的小球体,如题8-13图所示.试求:两球心 O 与 O 点的场强, 并证明小球空腔内的电场是均匀的. 解: 将此带电体看作带正电 的均匀球与带电 − 的均匀小球的组合,见 题 8-13 图(a). (1) + 球在 O 点产生电场 E10 = 0