(三)齿根弯曲疲劳强度计算(续) 式中:Ya一斜齿轮的齿形系数,可近似地按当量 齿数2v≈z/cos3B由表10-5查取; Ysa一斜齿轮的应力校正系数,可近似地按当量齿 数zv由表10-5查取; ■Y一螺旋角影响系数,数值查图10-28。 1.00 Ep=0 0.1 0.2 0.3 0.90 0.4 0.5 0.6 0.7 0.80 0.8 0.9 0.75- ≥1 10 20 30 40 P/() 图10-28螺旋角影响系数Y:
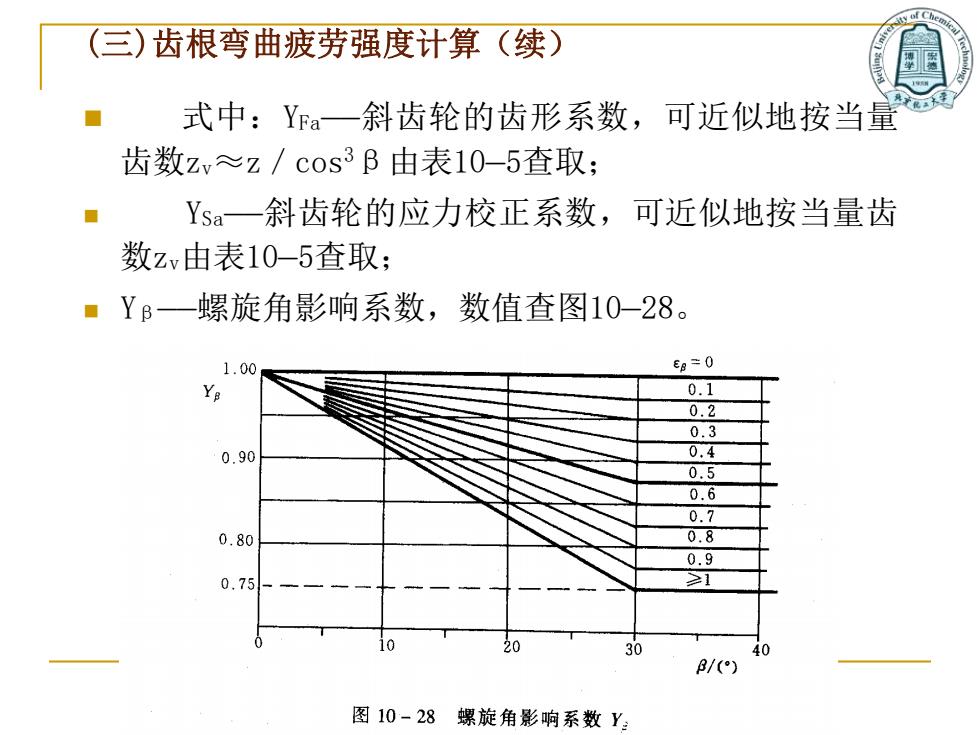
(三)齿根弯曲疲劳强度计算(续) ◼ 式中:YFa——斜齿轮的齿形系数,可近似地按当量 齿数zv≈z/cos3β由表10—5查取; ◼ YSa——斜齿轮的应力校正系数,可近似地按当量齿 数zv由表10—5查取; ◼ Yβ——螺旋角影响系数,数值查图10—28
V §10-7标准斜齿圆柱齿轮传动的强度计算(续) (四)齿面接触疲劳强度计算 OH= Pm.Ze≤[oH] 啮合平面 斜齿轮的齿面接触 疲劳强度仍按上式计算, 节点的综合曲率1/pΣ 仍按式(10-7)计算。 如图10-29所示,对于 渐开线斜齿圆柱齿轮, 在啮合平面内,节点P 基圆柱 处的法面曲率半径pn 与端面曲率半径pt的 关系由几何关系得 图10-29斜齿圆柱齿轮法面曲率半径
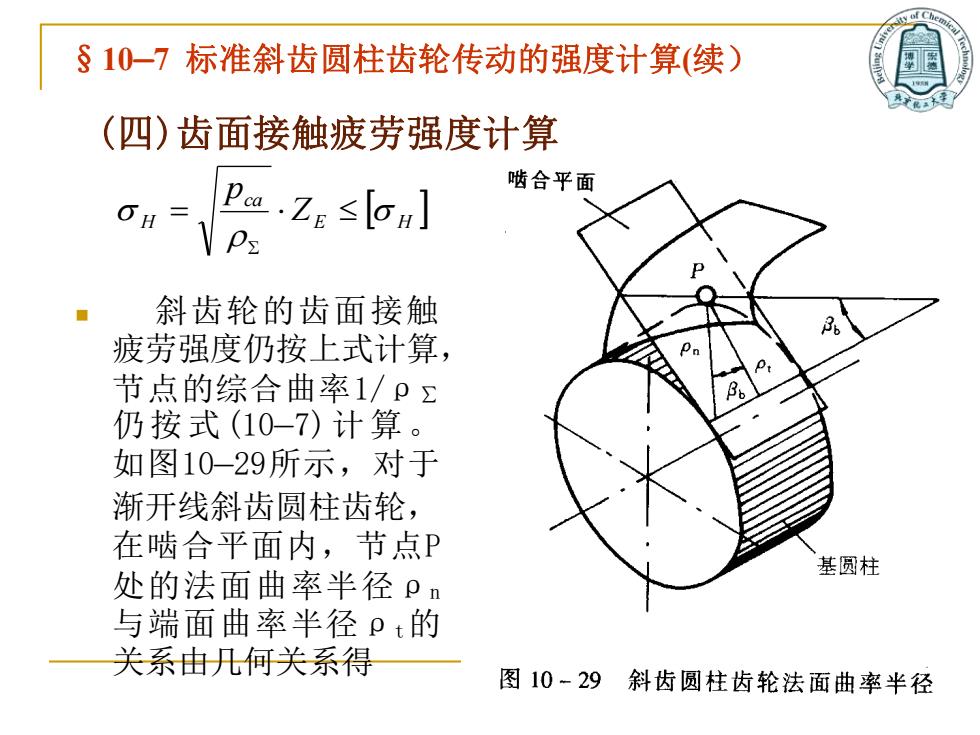
(四)齿面接触疲劳强度计算 ◼ 斜齿轮的齿面接触 疲劳强度仍按上式计算, 节点的综合曲率1/ρ∑ 仍按式(10—7)计算。 如图10—29所示,对于 渐开线斜齿圆柱齿轮, 在啮合平面内,节点P 处的法面曲率半径ρn 与端面曲率半径ρt的 关系由几何关系得 E H ca H Z p = §10—7 标准斜齿圆柱齿轮传动的强度计算(续)

(四)齿面接触疲劳强度计算(续) 合平 在啮合平面内,节点P处的法面曲率半 径p,与端面曲率半径p,的关系 cos B dsina, 斜齿轮端面上节点的曲率半径为 P,= 基村 2 图10-29斜齿柱齿轮法面曲率半径 1-1±1-2cosB±2cosB-2cosB。 ± Ps Pm pn2 d sin a ud sin a,d sin a, 将上式及式(10一15)代人式(106),得 KF 2cosf。 ba cosa d sina, KE 2w±1 bd Ea 2cosB,-Ze≤onJ sin a,cosa
(四)齿面接触疲劳强度计算(续) b t n cos = 2 sin t t d = = = = u u d ud d t b t b t b n n 1 sin 2cos sin 2cos sin 1 1 1 2cos 1 2 1 1 1 在啮合平面内,节点P处的法面曲率半 径ρn与端面曲率半径ρt的关系 斜齿轮端面上节点的曲率半径为 将上式及式(10—15)代人式(10—6),得 E H t t t b E t b t t E ca H Z u u bd KF Z u u b d KF Z p = = = sin cos 1 2cos 1 sin 2cos cos 1 1

(四)齿面接触疲劳强度计算(续) 令 Zu= 2cos B (10-19) sin a,cosa, Z称为区域系数。图10-30为法向压力角a,=20°的标准齿 轮的Z值。于是得 KF,u± .ZnZ≤om] (10-20)校核公式 bd sa u 2KT.u±1ZHZE (10-21)设计公式
(四)齿面接触疲劳强度计算(续) t t b Z H sin cos 2cos 令 = (10-19) ZH称为区域系数。图10—30为法向压力角α n =20°的标准齿 轮的ZH值。于是得 H E H t H Z Z u u bd KF = 1 1 3 2 1 1 2 1 H H E d Z Z u KT u d (10-20) 校核公式 (10-21)设计公式
(四)齿面接触疲劳强度计算(续) 对于斜齿圆柱 齿轮传动,因齿面 上的接触线是倾斜 的,所以在同一齿 面上就会有齿顶面 (其上接触线段为 eP)与齿根面(其 上接触线段为e2P) 同时参与啮合 图10-31斜齿轮齿面上的接触线
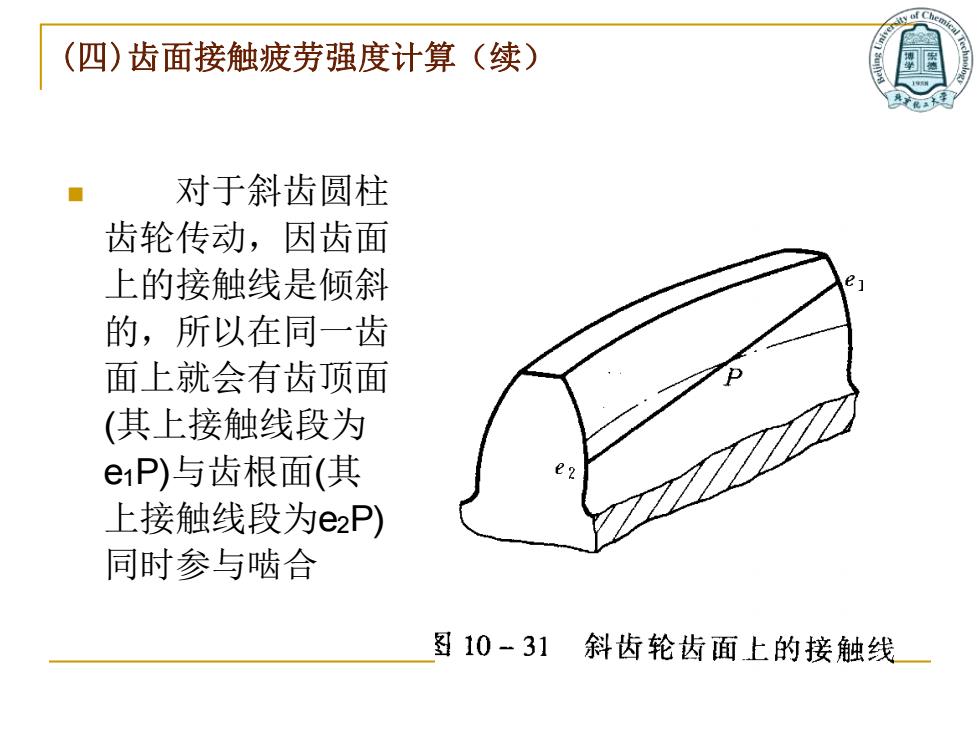
(四)齿面接触疲劳强度计算(续) ◼ 对于斜齿圆柱 齿轮传动,因齿面 上的接触线是倾斜 的,所以在同一齿 面上就会有齿顶面 (其上接触线段为 e1P)与齿根面(其 上接触线段为e2P) 同时参与啮合