
水压不应太大,待药物充分洗净后再就医。当眼睛里进入碎玻璃 或其它固体异物时,应闭上眼睛不要转动,立即到医务室就医。 2、浓酸、浓碱洒在衣服或皮肤上时,应立即用大量水冲洗 再分别用2%碳酸氢钠溶液或2%醋酸擦洗,用水冲洗后,外敷氧 化锌软膏(或硼酸软膏)。 3、不慎吸入煤气、溴蒸汽、氯气、氯化氢、疏化氢等气体时, 应立即到室外做深呼吸,呼吸新鲜空气。 4、当烫伤时,在烫伤处抹上黄色的苦味酸溶液或烫伤音,切 勿用水冲洗。 5、毒物误入口内,可取5~10mL稀硫酸铜溶液,加入一杯 温水中,内服后用食指伸入咽喉,促使呕吐,然后立即送医院治 疗。 6、人体触电时,应立即切断电源,或用非导体将电线从触电 者身上移开。如有休克现象,应将触电者移到有新鲜空气处立即 进行人工呼吸,并请医生到现场抢救。 7、实验过程中万一发生着火,应立即切断电源,移走易燃物 质等,防止火势漫延。灭火的方法要根据起火原因采用相应的方 法。一般的小火可用湿布、石棉布覆盖燃烧物灭火。火势大时可 使用泡沫灭火器。但电器设备引起的火灾,只能用四氯化碳灭火 器灭火。实验人员衣服着火时,切勿乱跑,应赶快脱下衣服,用 石棉布覆盖着火处,或者就地卧倒滚打,也可起到灭火的作用。 火势较大,应立即报火警。 四、误差与有效数字 (一)误差的基本概念 1、测量中的误差。 任何测量过程都包含着误差。按其性质的不同误差可分为三 类,即系统误差、偶然误差和过失误差。 (1)系统误差
3 水压不应太大,待药物充分洗净后再就医。当眼睛里进入碎玻璃 或其它固体异物时,应闭上眼睛不要转动,立即到医务室就医。 2、浓酸、浓碱洒在衣服或皮肤上时,应立即用大量水冲洗, 再分别用 2%碳酸氢钠溶液或 2%醋酸擦洗,用水冲洗后,外敷氧 化锌软膏(或硼酸软膏)。 3、不慎吸入煤气、溴蒸汽、氯气、氯化氢、硫化氢等气体时, 应立即到室外做深呼吸,呼吸新鲜空气。 4、当烫伤时,在烫伤处抹上黄色的苦味酸溶液或烫伤膏,切 勿用水冲洗。 5、毒物误入口内,可取 5~10mL 稀硫酸铜溶液,加入一杯 温水中,内服后用食指伸入咽喉,促使呕吐,然后立即送医院治 疗。 6、人体触电时,应立即切断电源,或用非导体将电线从触电 者身上移开。如有休克现象,应将触电者移到有新鲜空气处立即 进行人工呼吸,并请医生到现场抢救。 7、实验过程中万一发生着火,应立即切断电源,移走易燃物 质等,防止火势漫延。灭火的方法要根据起火原因采用相应的方 法。一般的小火可用湿布、石棉布覆盖燃烧物灭火。火势大时可 使用泡沫灭火器。但电器设备引起的火灾,只能用四氯化碳灭火 器灭火。实验人员衣服着火时,切勿乱跑,应赶快脱下衣服,用 石棉布覆盖着火处,或者就地卧倒滚打,也可起到灭火的作用。 火势较大,应立即报火警。 四、误差与有效数字 (一)误差的基本概念 1、测量中的误差。 任何测量过程都包含着误差。按其性质的不同误差可分为三 类,即系统误差、偶然误差和过失误差。 (1) 系统误差

也称可测误差,是由某些比较确定的原因引起的,它对测量 结果的影响比较固定,其大小有一定规律性,在重复测量时,会 重复出现。产生系统误差的主要原因有:实验方法不完善:所用 的仪器准确度差:药品不纯以及操作不当等。系统误差可以用改 善方法、校正仪器、提纯药品、做空白试验、对照试验的方法来 减少。有时也可以在找出误差原因后,算出误差的大小而加以修 正。 (2)偶然误差 也称随机误差或难测误差,由某些难以预料的偶然因素引起, 它对实验结果的影响不固定。由于偶然误差的原因难以确定,似 乎无规律性可寻,但如果多次测量,可以发现偶然误差遵从正态 分布,即大小相近的正负误差出现机会相等,小误差出现的概率 大,大误差出现的概率很小。因此,通过多次测量取平均值的方 法可以减少偶然误差对测量结果的影响。 (3)过失误差 这是一种与事实明显不符的误差,由分析过程中的器皿不洁、 加错试剂、错用样品、试样损失、仪器出现异常未被发现、读错 数据、计算错误等不应有的错误造成。过失误差无规律可循,但 只要加强责任心:工作认真细致即可避免。 2、准确度与误差 准确度系指在特定的条件下获得的分析结果与真实值之间的 符合程度。准确度由分析的偶然误差和系统误差决定,它能反映 分析结果的可靠性。要想提高分析结果的准确度,不仅需要改善 分析的精密度,同时要消除系统误差。 准确度用绝对误差或相对误差表示。绝对误差是指实验测得 的数值与真实值之间的差值:相对误差指绝对误差与真实值的百 分比。即 4
4 也称可测误差,是由某些比较确定的原因引起的,它对测量 结果的影响比较固定,其大小有一定规律性,在重复测量时,会 重复出现。产生系统误差的主要原因有:实验方法不完善;所用 的仪器准确度差;药品不纯以及操作不当等。系统误差可以用改 善方法、校正仪器、提纯药品、做空白试验、对照试验的方法来 减少。有时也可以在找出误差原因后,算出误差的大小而加以修 正。 (2)偶然误差 也称随机误差或难测误差,由某些难以预料的偶然因素引起, 它对实验结果的影响不固定。由于偶然误差的原因难以确定,似 乎无规律性可寻,但如果多次测量,可以发现偶然误差遵从正态 分布,即大小相近的正负误差出现机会相等,小误差出现的概率 大,大误差出现的概率很小。因此,通过多次测量取平均值的方 法可以减少偶然误差对测量结果的影响。 (3)过失误差 这是一种与事实明显不符的误差,由分析过程中的器皿不洁、 加错试剂、错用样品、试样损失、仪器出现异常未被发现、读错 数据、计算错误等不应有的错误造成。过失误差无规律可循,但 只要加强责任心;工作认真细致即可避免。 2、准确度与误差 准确度系指在特定的条件下获得的分析结果与真实值之间的 符合程度。准确度由分析的偶然误差和系统误差决定,它能反映 分析结果的可靠性。要想提高分析结果的准确度,不仅需要改善 分析的精密度,同时要消除系统误差。 准确度用绝对误差或相对误差表示。绝对误差是指实验测得 的数值与真实值之间的差值;相对误差指绝对误差与真实值的百 分比。即

相对误差=绝对误差×10% 真实值 绝对误差=测定值一真实值 绝对误差与被测量的大小无关,而相对误差却与被测量的大 小有关。一般来说,若被测的量越大,相对误差越小。一般用相 对误差来反映测定值与真实值之间的偏离程度比用绝对误差更为 合理。 3、精密度与偏差 精密度系指在一定条件下,重复分析同一样品所得测定值的 致程度,即测量结果的再现性,由分析的偶然误差决定。 通常被测量的真实值很难准确知道,因此,一般只能用多次 重复测量结果的平均值代替真实值。这时单次测量结果与平均值 之间的偏离就称为偏差。偏差与误差一样也有相对偏差与绝对偏 差。 绝对偏差=单次测定值一平均值 相对偏差=绝对偏差x10% 平均值 石.三水-,Ra.x100%日为平均偏差,Ri为相对平均偏差) 从相对偏差的大小可以反映出测量结果再现性的好坏,即测 量的精密度。相对偏差小,则可视为再现性好,即精密度高。在 般的化学实验中,一般可以用平均偏差或相对平均偏差表示。 4、提高测量结果准确度的方法 为了提高测量结果的准确度。应尽量减小系统误差、偶然误 差和过失误差。认真仔细地进行多次测量,取其平均值作为测量 结果,这样可以减少系统误差。减少系统误差的方法一般有:校 正测量仪器与测量方法、空白试验与对照试验。 5
5 绝对误差=测定值-真实值 绝对误差与被测量的大小无关,而相对误差却与被测量的大 小有关。一般来说,若被测的量越大,相对误差越小。一般用相 对误差来反映测定值与真实值之间的偏离程度比用绝对误差更为 合理。 3、精密度与偏差 精密度系指在一定条件下,重复分析同一样品所得测定值的 一致程度,即测量结果的再现性,由分析的偶然误差决定。 通常被测量的真实值很难准确知道,因此,一般只能用多次 重复测量结果的平均值代替真实值。这时单次测量结果与平均值 之间的偏离就称为偏差。偏差与误差一样也有相对偏差与绝对偏 差。 绝对偏差=单次测定值—平均值 从相对偏差的大小可以反映出测量结果再现性的好坏,即测 量的精密度。相对偏差小,则可视为再现性好,即精密度高。在 一般的化学实验中,一般可以用平均偏差或相对平均偏差表示。 4、提高测量结果准确度的方法 为了提高测量结果的准确度。应尽量减小系统误差、偶然误 差和过失误差。认真仔细地进行多次测量,取其平均值作为测量 结果,这样可以减少系统误差。减少系统误差的方法一般有:校 正测量仪器与测量方法、空白试验与对照试验。 = 100% 真实值 绝对误差 相对误差 100% (d Rd ) x d , Rd n x x d i = 为平均偏差, 为相对平均偏差 − = = 100% 平均值 绝对偏差 相对偏差
(二)有效数字 1、有效数字位数的确定 分析测试中,在记录测定数据时,用来表示测定结果的数值 所表示的准确程度应与测试时所用的测量仪器及测试方法的精度 相一致。通常测定时,一般可估计到测量仪器最小刻度的十分位, 在记录测定数据时,只应保留一位不确定数字,其余数字都应是 准确的,通常称此时所记录的数字为有效数字。记录和报告的测 定结果只应包含有效数字,对有效数字的位数不能任意增删。 化学实验中常用仪器的精度与实测数据有效数字位数的关系 列于表11中。 表I-1常用仪器的精度与实测值有效数字位数 仪器名称 仪器精度 真实值 有效数字 错误举例 位数 托盘天平 0.1g 12.3g 3 12.30g 电光天平 0.0001g 12.3456g 6 12.345g 10mL量筒 0.1ml 7.2mL 2 7mL 100mL量筒 1mL 72mL 2 72.5mL 滴定管 0.01mL 23.00mL 23.0mL 移液管 0.01mL 25.00mL 4 25mL 容量瓶 0.01mL 50.00mL A 50mL 任意超出或低于仪器精度的数字都是不恰当的。例如上述电 光天平的读数为12.3456g,既不能读作12.345g,也不能读作 12.34567g,因为前者降低了实验的精确度,后者则夸大了实验的 精确度。 关于有效数字位数的确定,还应注意以下几点: (1)数字“0”在数据中具有双重意义。若作为普通数字使用, 它就是有效数字:若它只起定位作用,就不是有效数字。例如在 分析天平上称得重铬酸钾的质量为0.0758g,此数据具有三位有效 数字,数字前面的“0”只起定位作用,不是有效数字。又如某盐 6
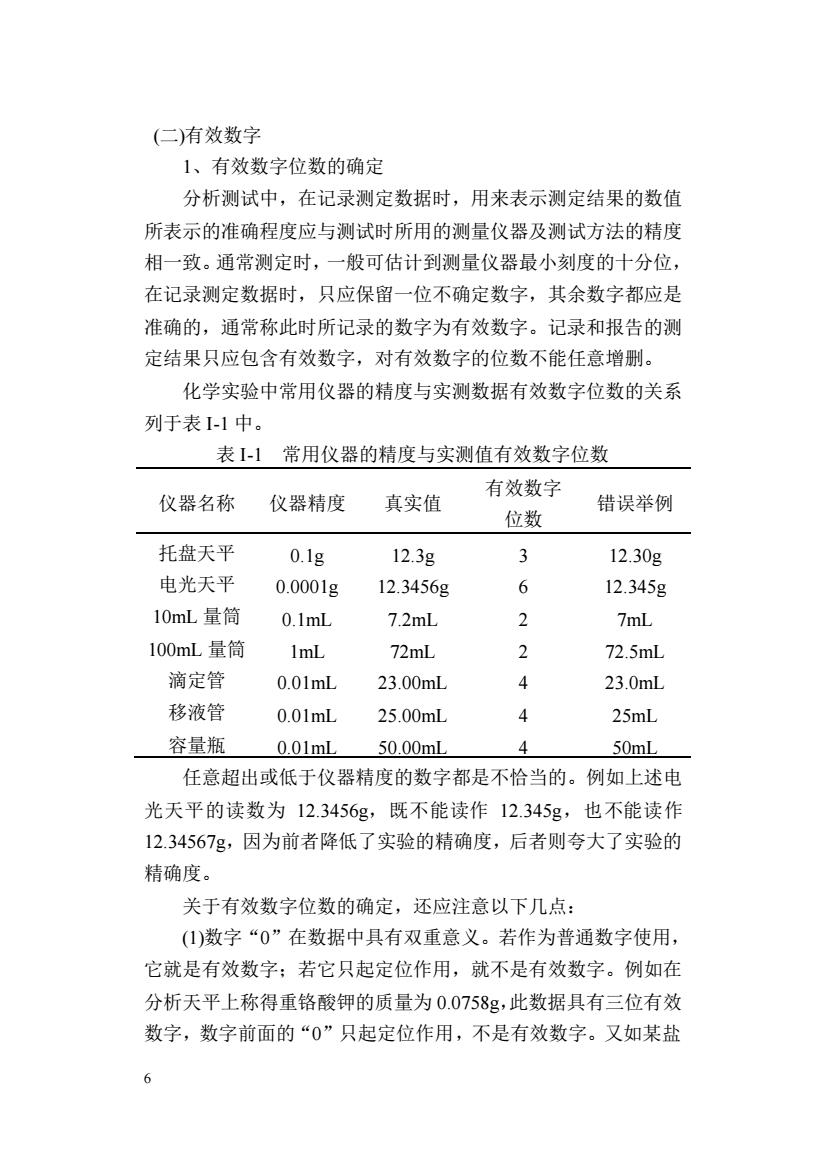
6 (二)有效数字 1、有效数字位数的确定 分析测试中,在记录测定数据时,用来表示测定结果的数值 所表示的准确程度应与测试时所用的测量仪器及测试方法的精度 相一致。通常测定时,一般可估计到测量仪器最小刻度的十分位, 在记录测定数据时,只应保留一位不确定数字,其余数字都应是 准确的,通常称此时所记录的数字为有效数字。记录和报告的测 定结果只应包含有效数字,对有效数字的位数不能任意增删。 化学实验中常用仪器的精度与实测数据有效数字位数的关系 列于表 I-1 中。 表 I-1 常用仪器的精度与实测值有效数字位数 仪器名称 仪器精度 真实值 有效数字 位数 错误举例 托盘天平 0.1g 12.3g 3 12.30g 电光天平 0.0001g 12.3456g 6 12.345g 10mL 量筒 0.1mL 7.2mL 2 7mL 100mL 量筒 1mL 72mL 2 72.5mL 滴定管 0.01mL 23.00mL 4 23.0mL 移液管 0.01mL 25.00mL 4 25mL 容量瓶 0.01mL 50.00mL 4 50mL 任意超出或低于仪器精度的数字都是不恰当的。例如上述电 光天平的读数为 12.3456g,既不能读作 12.345g,也不能读作 12.34567g,因为前者降低了实验的精确度,后者则夸大了实验的 精确度。 关于有效数字位数的确定,还应注意以下几点: (1)数字“0”在数据中具有双重意义。若作为普通数字使用, 它就是有效数字;若它只起定位作用,就不是有效数字。例如在 分析天平上称得重铬酸钾的质量为 0.0758g,此数据具有三位有效 数字,数字前面的“0”只起定位作用,不是有效数字。又如某盐

酸溶液的浓度(0.2100mol·Ll)准确到小数点第三位,第四位可能 有士1的误差,所以这两个“0”是有效数字,数据02100具有四 位有效数字。 (2)改变单位并不改变有效数字的位数,如滴定管读数 12.34mL,,若该读数改用升为单位,则是0.01234L,这时前面的 两个零只起定位作用,不是有效数字,0.01234L与12.34mL一样 都是四位有效数字。当需要在数的末尾加“0”作定位作用时,最 好采用指数形式表示,否则有效数字的位数含混不清。例如,质 量为25.08若以毫克为单位,则可表示为2.50×104mg:若表示为 25000mg,就易误解为五位有效数字。 (3)对数值有效数字位数,仅由小数部分的位数决定,首数(整 数部分)只起定位作用,不是有效数字。因此对数运算时,对数小 数部分的有效数字位数应与相应的真数的有效数字位数相同。例 如:pH=2.38,H门=4.2×103的有效数字为二位,而不是三位。 2、有效数字的运算规则 在分析测定过程中,往往要经过几个不同的测量环节,例如 先用减量法称取试样,经过处理后进行滴定。在此过程中最少要 取四次数据,但这四个数据的有效数字位数不一定完全相等,在 进行运算时,应按照下列计算规则,合理地取舍各数字的有效数 字的位数,确保运算结果的正确。 (1)记录数据时,只保留一位有效数字。当拟舍弃的数字大于 等于6时进位,而当尾数恰为5时,则看保留的末位数是奇数还 是偶数,是奇数时就将5进位,是偶数时,则将5舍弃。总之, 使保留下来的末位数是偶数,即“四舍六入五留双”。根据此原则 如将4.175和4.165处理成三位数,则分别为4.18和4.16。 (2)进行数值加减时,最后结果所保留小数点后的位数应与参 与运算的各数中小数点后位数最少者相同。例如 1
7 酸溶液的浓度(0.2100mol•L -1 )准确到小数点第三位,第四位可能 有±1 的误差,所以这两个“0”是有效数字,数据 0.2100 具有四 位有效数字。 (2)改变单位并不改变有效数字的位数,如滴定管读数 12.34mL,若该读数改用升为单位,则是 0.01234L,这时前面的 两个零只起定位作用,不是有效数字,0.01234L 与 12.34mL 一样 都是四位有效数字。当需要在数的末尾加“0”作定位作用时,最 好采用指数形式表示,否则有效数字的位数含混不清。例如,质 量为 25.08 若以毫克为单位,则可表示为 2.50×104mg;若表示为 25000mg,就易误解为五位有效数字。 (3)对数值有效数字位数,仅由小数部分的位数决定,首数(整 数部分)只起定位作用,不是有效数字。因此对数运算时,对数小 数部分的有效数字位数应与相应的真数的有效数字位数相同。例 如:pH=2.38,[H+ ] = 4.2×10-3 的有效数字为二位,而不是三位。 2、有效数字的运算规则 在分析测定过程中,往往要经过几个不同的测量环节,例如 先用减量法称取试样,经过处理后进行滴定。在此过程中最少要 取四次数据,但这四个数据的有效数字位数不一定完全相等,在 进行运算时,应按照下列计算规则,合理地取舍各数字的有效数 字的位数,确保运算结果的正确。 (1)记录数据时,只保留一位有效数字。当拟舍弃的数字大于 等于 6 时进位,而当尾数恰为 5 时,则看保留的末位数是奇数还 是偶数,是奇数时就将 5 进位,是偶数时,则将 5 舍弃。总之, 使保留下来的末位数是偶数,即“四舍六入五留双”。根据此原则, 如将 4.175 和 4.165 处理成三位数,则分别为 4.18 和 4.16。 (2)进行数值加减时,最后结果所保留小数点后的位数应与参 与 运 算 的 各 数 中 小 数 点 后 位 数 最 少 者 相 同 。 例 如