
§2-3典型一维稳态导热问题的分析解 稳态导热: Ot 直角坐标系:。(U) (2)+q.-0 圆柱坐标系:, 一、 通过平壁的导热 假设:长度和宽度远大于厚度δ 简化为一维导热问题 a)导热微分方程: +9,=0
一 、通过平壁的导热 §2-3 典型一维稳态导热问题的分析解 : = 0 t 稳态导热 直角坐标系: ( ) ( ) ( ) + = 0 + + v q z t y z t x y t x 圆柱坐标系: ( ) ( ) 0 1 ( ) 1 2 + = + + v q z t z t r r t r r r o x 假设:长度和宽度远大于厚度 — 简化为一维导热问题 a) 导热微分方程: ( ) + = 0 v q d x dt d x d

b)几何条件:单层或多层;δ c)物理条件:p、c、2已知;有或无内热源 d)时间条件:稳态导热:ot/ax=0 e)边界条件:第一类:已知iv 第三类:已知h,t dx dx 1、第一类边界条件下通过平壁的一维稳态导热 (①)单层平壁 a)入为常数、无内热源时: dt=0 x=0,t=tyl dx2-0 x=δ,t=tw2 w2 直接积分,得: dt =C1→t=Cx+C2 dx
1、第一类边界条件下通过平壁的一维稳态导热 b) 几何条件:单层或多层; c) 物理条件:、c、 已知;有或无内热源 e) 边界条件:第一类:已知 tw 第三类:已知 h, t f (1) 单层平壁 a) 为常数、无内热源时: d) 时间条件: 稳态导热 :t = 0 o x tw1 t tw2 = = = = = 2 1 2 2 , 0, 0 w w x t t x t t d x d t 直接积分,得: 1 1 2 c t c x c d x d t = = + ( ) + qv = 0 d x dt d x d

根据边界条件,得: C2 =tw;C=(tw2 -twm)/8 平壁内温度分布: 线性分布 t=2nx+1=-(6-i2) δ 导过平壁的热流量: dx δ/2A R R,=6(24)-导热面积为4时导热热阻[C/W 热流密度: 9-g-22wm δ/九 r,=δ/2-单位面积上导热热阻m2C/w
导过平壁的热流量: 根据边界条件,得: 平壁内温度分布: 热流密度: c2 = t w1 ; c1 = (t w2 − t w1 ) x x t t t t t t t w w w w w w ( ) 1 1 1 2 2 1 + = − − − = 线性分布 W 1 2 1 2 1 2 R t t A t t t t A d x d t Φ A w w w w w − w = − = − = − = R A A C W = ( ) −导热面积为 时导热热阻 1 2 1 2 1 2 2 W m r t t t t t t A Q q w w w w w − w = − = − = = m C W 单位面积上导热热阻 2 r = −
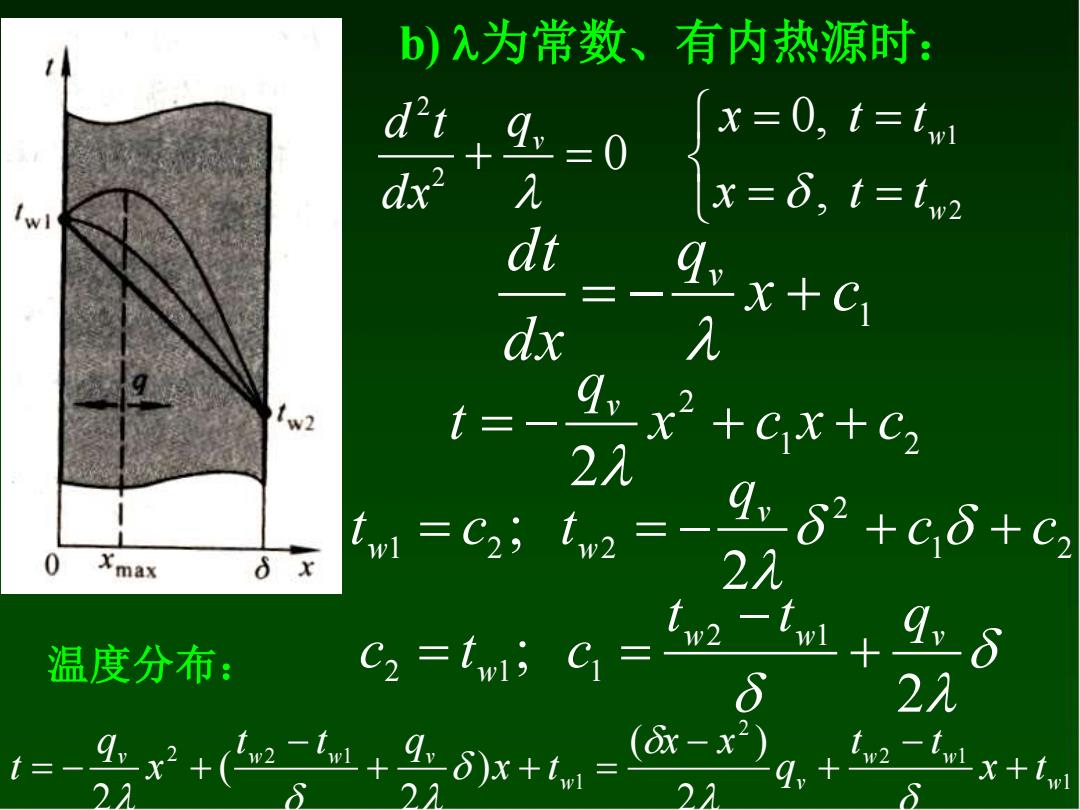
b)入为常数、有内热源时: d'"t =0 x =0,t=twl 山一小 x=δ,t=tw2 9 x+C1 2 t 2+cx+C2 2λ 0 Xmax 6 x =c:=-号28+c6+c9 2元 温度分布: C2=t C= 2元 t=- 2 +(+号x+=
b) 为常数、有内热源时: = = = = + = 2 1 2 2 , 0, 0 w v w x t t q x t t d x d t 1 x c q d x dt v = − + 1 2 2 2 x c x c q t v = − + + 1 2 2 1 2 2 2 ; c c q t c t v w = w = − + + 2 ; 2 1 2 1 1 w w v w t t q c t c + − = = 1 2 1 2 1 2 2 1 2 ( ) ) 2 ( 2 w w w w v v w w v x t t t q x x x t t t q x q t + − + − + + = − = − + 温度分布:

1 温度分布: t=、 ,-是+ 22 (6x-x 2g+x+ 2λ 热流密度: 0 Xmax 6 x 当没有内热源时:4,=0:1=-2x
1 2 1 2 1 2 2 1 2 ( ) ) 2 ( 2 w w w v w v w w v x t t t q x x x t t t q x q t + − + − = + + − = − + 温度分布: − + − = − = − 2 1 2 ( 2 ) d d w w v t t q x x t q 热流密度: x t t q t t w w v w 1 2 1 0 − 当没有内热源时: = ; = −