山西能源学院：《传热学》课程教学资源（PPT课件）第五章 对流传热的理论基础（2/2）

Ou 边界层换热 Ox d "Oy 微分方程组 at ∂2t +V y 解的函数形式 特征数关联式 特征数是由一些物理量组成的无量纲数，例如毕渥 数B和付里叶数Fo。对流换热的解也可以表示成特征数 函数的形式，称为特征数关联式。 通过对流换热微分方程的无量纲化可以导出与对流 换热有关的特征数

2 解的函数形式——特征数关联式 0 u v x y     + = 2 2 u u du u u v u x y dx y         + = +  t t u v x y     + 2 2 t a y   = 特征数是由一些物理量组成的无量纲数，例如毕渥 数Bi和付里叶数Fo。对流换热的解也可以表示成特征数 函数的形式，称为特征数关联式。 通过对流换热微分方程的无量纲化可以导出与对流 换热有关的特征数。 边 界 层 换 热 微分方程组

引进下列无量纲变量： U -1 X- X一 对流换热表面传热系数与温度场之间的关系式 1 (t,ts)8 tw-tOy (t-t) lr=o 1 aY hl hl Nu ay y=0 Nu Y 7=0 N称为平均努塞尔数，等于壁面法线方向上的无 量纲温度梯度，大小反映平均对流换热的强弱

3 Nu称为平均努塞尔数，等于壁面法线方向上的无 量纲温度梯度，大小反映平均对流换热的强弱。 w y 0 t h t t y     = = − − 引进下列无量纲变量： Y 0 l Y    = = ( ) ( w ) w Y 0 t t h t t l Y      = − = − − Y 0 hl Y    = = Y 0 Nu Y   = = w w , , , , x y u v t t X Y U V l l u u t t     − = = = = = − 对流换热表面传热系数与温度场之间的关系式 hl Nu  令 =

对于常物性、无内热源、不可压缩牛顿流体平行 外掠平板稳态对流换热，duldx=0,方程组简化为 Ov 无量纲化 OX ay O-u U 1∂2U + Y Re Oy2 2⊙ Y Re.Pr OY2 式中Re = u 称为雷诺数。由无量纲方程组可以看出： U=f(X,Y,Re) V=f(X,Y,Re) ⊙=f(X,Y,Re,Pr) a0 再由Nu= Nu=f(Re,Pr) Nu待定特征数 Y=0 Re,Pr已定特征数

4 0 u v x y     + = 2 2 u u u u v x y y        + = t t u v x y     + 2 2 t a y   = 0 U V X Y     + = 2 2 U U U 1 U V X Y Re Y       + = 2 2 1 U V X Y Re Pr Y        + =  对于常物性、无内热源、不可压缩牛顿流体平行 外掠平板稳态对流换热，du / /dx=0，方程组简化为 无量纲化 式中 u l Re   = 称为雷诺数。由无量纲方程组可以看出： U f X Y Re = ( , , ) V f X Y Re = ( , , )  = f X Y Re,Pr ( , , ) Y 0 Nu Y   = 再由 = Nu f Re Pr = ( , ) Nu 待定特征数 Re,Pr已定特征数

可见，流体平行外掠平板强迫对流换热的解可以表 示成式特征数关联式的形式，即 Nu=f(Re,Pr) 对比h=f(u,tw,t,2,p,c,n,a,l,y 特征数关联式中变量个数大为减少，更突出地反映相关 物理量之间的依赖关系及其对对流换热的综合影响。 5.4流体外掠平板层流边界层微分方程精确解 对于常物性、 无内热源、不可压 =0 2斤1=0 缩牛顿流体平行外 t=tw 掠等壁温平板稳态 x 1 u-Voo 层流(Re≤5×105 t=too> 换热，数学模型为

5 5.4 流体外掠平板层流边界层微分方程精确解 可见，流体平行外掠平板强迫对流换热的解可以表 示成式特征数关联式的形式，即 Nu f Re Pr = ( , ) 特征数关联式中变量个数大为减少，更突出地反映相关 物理量之间的依赖关系及其对对流换热的综合影响。 对比 h f u t t c l = ( , , , , , , , , , w f      ) 对于常物性、 无内热源、不可压 缩牛顿流体平行外 掠等壁温平板稳态 层流（Re≤5×105） 换热，数学模型为： 0 u v x y     + = 2 2 u u u u v x y y        + = t t u v x y     + 2 2 t a y   = y = 0, u=v=0, t = tw , y =∞ , u=u∞ , t = t∞

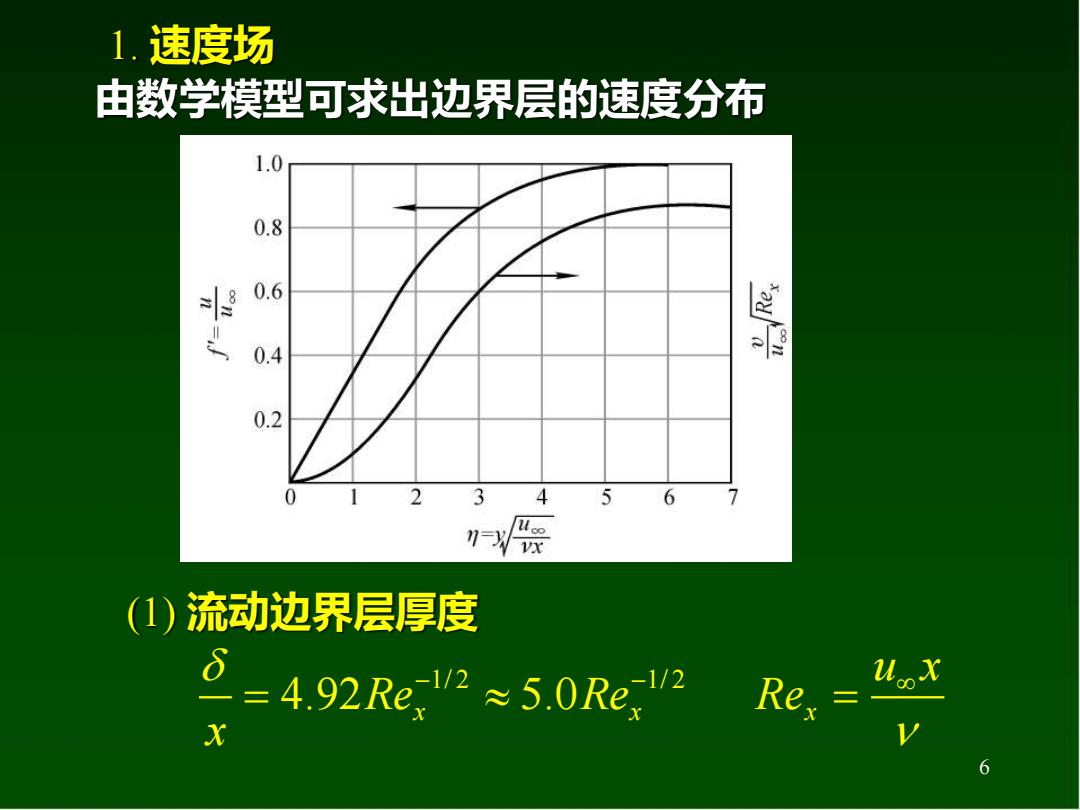
1.速度场 由数学模型可求出边界层的速度分布 1.0 0.8 第 0.4 0.2 0 2 3 4 5 6 (1)流动边界层厚度 D=4,92Re:2≈5.0Re2 Res= uox X 6

6 1. 速度场 1/ 2 1/ 2 4.92 5.0 Re Re x x x  − − =  x u x Re   = (1) 流动边界层厚度 由数学模型可求出边界层的速度分布