
北京化工大学2005一一2006学年第一学期 《计算化学》期末考试试卷标准答案 1. 计算原理(化学原理和计算方法)(20分) 苯为低沸点组分。按题意将数值代入方程 (1) 式(1)中,F=F。/2,a=2.5,0=0.6 (5分) 整理后得 2.5ln(1-x)-ln(x)+0.7402=0 令f(x)=2.5ln(1-x)-ln(x)+0.7402 (5分) f(x)的一阶导数容易求得 f(x)=-1-xx 251 (5分) 故可调用Newton-Raphson法求解方程f(x)=0 此处,取初值=0.4,可求出x。其中调用函数子程序计算f(x)、f"(x)值。(5分) 程序框图(30分) 开始 输入已知变量:F=F。/2,a=2.5,x0=0.6(5分) 取初值=0.4(5分)N)
1 北京化工大学 2005——2006 学年第一学期 《计算化学》期末考试试卷标准答案 A 1. 计算原理(化学原理和计算方法)(20 分) 苯为低沸点组分。按题意将数值代入方程 ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − − + − = 0 0 0 1 1 ln ln 1 1 ln x x a x x F a F (1) 式(1)中, 0 F F = / 2 ,a=2.5,x0=0.6。 (5 分) 整理后得 2.5ln(1 ) ln( ) 0.7402 0 − x x −+ = 令 fx x x ( ) 2.5ln(1 ) ln( ) 0.7402 = −− + (5 分) f ( ) x 的一阶导数容易求得 2.5 1 ( ) 1 f x x x ′ =− − − (5 分) 故可调用 Newton-Raphson 法求解方程 f (x) = 0 此处,取初值=0.4,可求出 x。其中调用函数子程序计算 f ( ) x 、 f ′(x) 值。(5 分) 2. 程序框图(30 分) 开始 输入已知变量: 0 F F = / 2 ,a=2.5,x0=0.6 (5 分) 取初值=0.4(5 分)N)

调用Newton-Raphson法子程序求解方程f(x)=O (其中调用函数子程序计算f(x)、f"(x)值)得x(15分) 输出:残液中苯的含量x(5分) 结束 3. 源程序(30分) MAIN (15分) .X.X00.X0 EPS=IE-6 END (5分) LA XO F=2.5L0G1-XL0GX+0.7402 RETURN END FUNCTION G(X) (5分) A XO G=2.51-x1N RETURN END SUBROUTINE NEWN(XO,EPS,F.GX) (5分) REAL XO,EPS = 10 EX=F(XO) GX=GOXO) X=X0-FX/GX IF((ABS(X-X0)X).GT.EPS)THEN
2 3. 源程序(30 分) PROGRAM MAIN (15 分) REAL A,X,X00,X0 EXTERNAL F,G COMMON A,X0 A=2.5 X0=0.6 X00=0.4 EPS=1E-6 CALL NEWN(X00,EPS,F,G,X) WRITE(*,*)'X=',X END FUNCTION F(X) (5 分) REAL A,X0 COMMON A,X0 F=2.5*LOG(1-X)-LOG(X)+0.7402 RETURN END FUNCTION G(X) (5 分) REAL A,X0 COMMON A,X0 G=-(2.5/(1-X))-1/X RETURN END SUBROUTINE NEWN(X0,EPS,F,G,X) (5 分) REAL X0,EPS K=1 10 FX=F(X0) GX=G(X0) X=X0-FX/GX IF((ABS(X-X0)/X).GT.EPS)THEN 调用 Newton-Raphson 法子程序求解方程 f (x) = 0 (其中调用函数子程序计算 f ( ) x 、 f ′(x) 值)得 x(15 分) 输出:残液中苯的含量 x(5 分) 结束
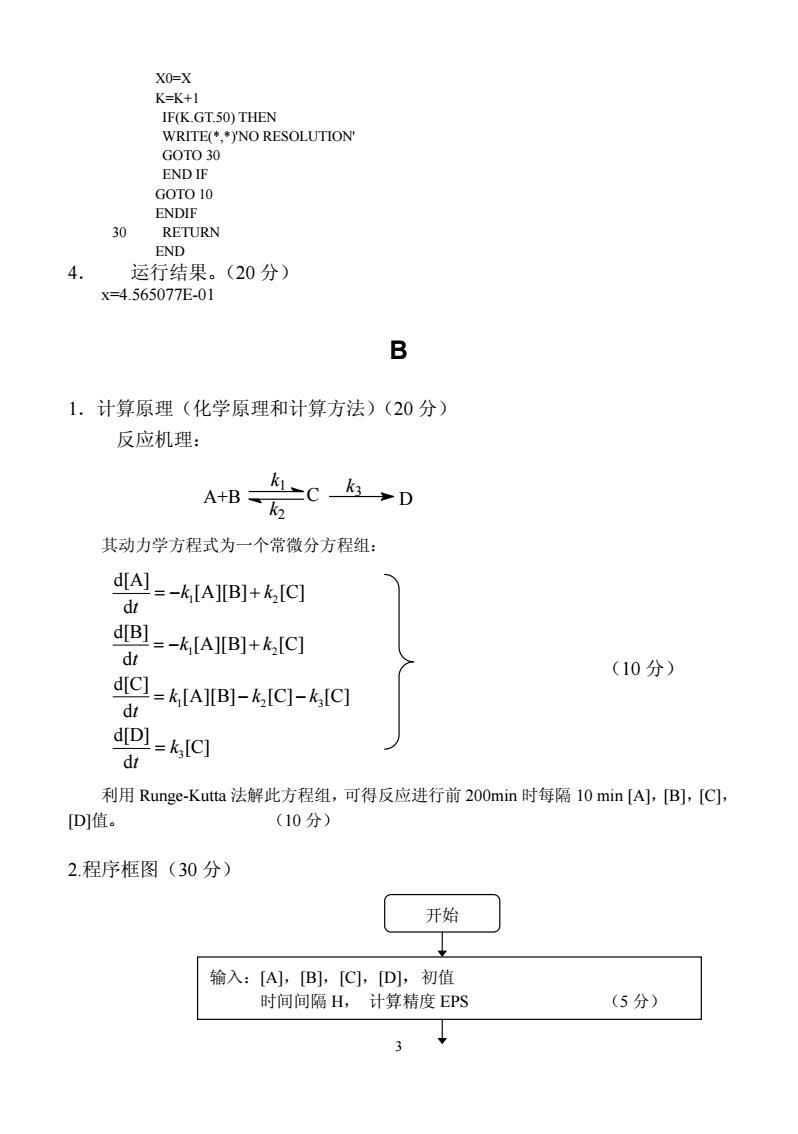
*N( GOTO 10 ENDIE RETURN EN 4. 运行结果。(20分) x=4.565077E-01 B 1.计算原理(化学原理和计算方法)(20分) 反应机理: AB会CD 其动力学方程式为一个常微分方程组: d[A]=-&[A][B]+&[C] dt d[B]=-k;[A][B]+k[C] (10分) dIC]-[A][B]-&IC]-k,IC] dt [D]=&[C] d 利用Runge-Kuta法解此方程组,可得反应进行前20Omin时每隔10min[A],B],[C, D值。 (10分) 2.程序框图(30分) 开始 输入:[A,B],[C],D,初值 时间间隔H,计算精度EPS (5分) 3
3 X0=X K=K+1 IF(K.GT.50) THEN WRITE(*,*)'NO RESOLUTION' GOTO 30 END IF GOTO 10 ENDIF 30 RETURN END 4. 运行结果。(20 分) x=4.565077E-01 B 1.计算原理(化学原理和计算方法)(20 分) 反应机理: A+B C k1 k2 D k3 其动力学方程式为一个常微分方程组: 1 2 1 2 1 23 3 d[A] [A][B] [C] d d[B] [A][B] [C] d d[C] [A][B] [C] [C] d d[D] [C] d k k t k k t k kk t k t =− + =− + = −− = (10 分) 利用 Runge-Kutta 法解此方程组,可得反应进行前 200min 时每隔 10 min [A],[B],[C], [D]值。 (10 分) 2.程序框图(30 分) 开始 输入:[A],[B],[C],[D],初值 时间间隔 H, 计算精度 EPS (5 分)

计算:积分步长H0(5分) 调用定步长Runge-.Kutta法子程序解动力学方程组计算时刻t的[A, B],[C],D]值 (其中调用计算动力学方程组的子程序计算DY值)(15分) 列表输出:反应进行前200min中每隔10min时所对应的 [A],B],[C],D值 (5分) 结束 3.源程序(30分) PROGRAM MAIN (15分) IMPLICIT REAL*8(A-H,O-Z) DIMENSION YO(10),Y1(10),Y2(10) OPEN(6.FILE-2006TESTB.TXT,STATUS-UNKNOWN) DATY0/0.05,0.1,0.0,0.0,60.0/ N=4 T0-0.0 T1=100.0 H0=10 EPS=1.0E-6 H=HO WRITE(6,11)N.TO,TI,HO,EPS WRITE(6,22)TO.H.(Y0(D).I=1.N) M=IDINT((T T0)WH0+10) D080I0=1, K- .Y1.H0.N.K) D030 KK=1,10 -K n1-1 10 ABS DO Y2 TE(6. 0 T0=T0+H0
4 3.源程序(30 分) PROGRAM MAIN (15 分) IMPLICIT REAL *8(A-H,O-Z) DIMENSION Y0(10),Y1(10),Y2(10) OPEN(6,FILE='2006TESTB.TXT',STATUS='UNKNOWN') DATA Y0/0.05,0.1,0.0,0.0,6*0.0/ N=4 T0=0.0 T1=100.0 H0=10 EPS=1.0E-6 H=H0 WRITE(6,11)N,T0,T1,H0,EPS WRITE(6,22)T0,H,(Y0(I),I=1,N) M=IDINT((T1-T0)/H0+10) DO 80 I0=1,M K=1 CALL RK4(T0,Y0,Y1,H0,N,K) DO 30 KK=1,100 K=K+K H=H0/K CALL RK4(T0,Y0,Y2,H,N,K) ES=0.0 DO 10 J=1,N 10 ES=ES+ABS((Y2(J)-Y1(J))/Y2(J)) IF(ES.LT.EPS)GOTO 50 DO 20 J=1,N 20 Y1(J)=Y2(J) 30 CONTINUE WRITE(6,33) STOP 50 T0=T0+H0 计算:积分步长 H0 (5 分) 调用定步长Runge-Kutta法子程序解动力学方程组计算时刻t的[A], [B],[C],[D]值 (其中调用计算动力学方程组的子程序计算 DY 值) (15 分) 列表输出:反应进行前 200min 中每隔 10min 时所对应的 [A],[B],[C],[D]值 (5 分) 结束

D060J=1N 60 6.22T0,HY20,=1,N 80 FORMAT(/Ix.N-.I2.2X.T0-.F6.1.2X.Tl-F8.12X. H0- G8.3.lX.EPS- 103 234 1X,96(1 3X Dmoll-1 6X'IBVmolL-16X'IC 1X961H-) FORMATUIX 2E8 22X 4G156) 3 FORMAT(/1X,'FAILED TO FIND STABLE SOLUTION IN MAX IT/) 4 END SUBROUTINE FCYDYY (5分) IMPLICIT REAL *8(A-H.O-Z) DEAI RKIK2K2 DIMENSION YUODYGON DATA K10.13/.K2J0.0491/.K3/0.11/ DY(1=K1*Y1)*Y2+K2*Y(3) DYCEKPY0Y(2)+K2*YG) DY(3=K1*YI)Y(2K2Y3K3*Y(3) DY4=K3*Y3) RETURN END SUBROUTINERK4(X0.Y0,Y.H,N.M) (10分) IMPLICIT REAL *8(A-H.O-Z) DIMENSION YO(N).Y(N) DIMENSION Y2(20).DY(20).RK(20) X=X0 D05I=1,N Y(IEYOD) DO 50L=1 M CALL ECYDYY Do101=1N RK(EDY(D 10 Y2(=Y①0.5*H*DY(D CALL F(Y2,DY) DO20I=IN RKI=RK①+2*DYD) 20 Y2=Y(①+0.5*H*DY④ CALL F(Y2,DY) D0301=1N RKI=RK①+2*DY① 30 Y2(D)=Y(D)+H*DY(I) CALL F(Y2,DY) D040=1,N RK(I-RK①HDYO
5 DO 60 J=1,N 60 Y0(J)=Y2(J) WRITE(6,22)T0,H,(Y2(I),I=1,N) 80 CONTINUE WRITE(6,44) 11 FORMAT(/1X,'N=',I2,2X,'T0=',F6.1,2X,'T1=',F8.1,2X, & 'H0=',G8.3,1X,'EPS=',G10.3//20X,'Y(I),I=1,2,3,4,...,N'//& 1X,96(1H-)/5X,'t/min',3X,'H/min',6X,'[A]/molL-1', & 6X,'[B]/molL-1',6X,'[C]/molL-1',6X,'[D]/molL-1'& /1X,96(1H-)) 22 FORMAT(1X,2F8.2,2X,4G15.6) 33 FORMAT(/1X,'FAILED TO FIND STABLE SOLUTION IN MAX IT'/) 44 FORMAT(1X,96(1H-)) END SUBROUTINE F(Y,DY) (5 分) IMPLICIT REAL *8(A-H,O-Z) REAL *8 K1,K2,K3 DIMENSION Y(10),DY(10) DATA K1/0.13/,K2/0.0491/,K3/0.11/ DY(1)=-K1*Y(1)*Y(2)+K2*Y(3) DY(2)=-K1*Y(1)*Y(2)+K2*Y(3) DY(3)=K1*Y(1)*Y(2)-K2*Y(3)-K3*Y(3) DY(4)=K3*Y(3) RETURN END SUBROUTINE RK4(X0,Y0,Y,H,N,M) (10 分) IMPLICIT REAL *8(A-H,O-Z) DIMENSION Y0(N),Y(N) DIMENSION Y2(20),DY(20),RK(20) X=X0 DO 5 I=1,N 5 Y(I)=Y0(I) DO 50 L=1,M CALL F(Y,DY) DO 10 I=1,N RK(I)=DY(I) 10 Y2(I)=Y(I)+0.5*H*DY(I) CALL F(Y2,DY) DO 20 I=1,N RK(I)=RK(I)+2*DY(I) 20 Y2(I)=Y(I)+0.5*H*DY(I) CALL F(Y2,DY) DO 30 I=1,N RK(I)=RK(I)+2*DY(I) 30 Y2(I)=Y(I)+H*DY(I) CALL F(Y2,DY) DO 40 I=1,N RK(I)=RK(I)+DY(I)