
第五章卷积码的译码算法 第五章卷积码的译码算法 卷积编码器自身具有网格结构,基于此结构我们给出两种译码算法:Viterbi译码算法和 BCJR译码算法。基于某种准则,这两种算法都是最优的。1967年,Viterbi提出了卷积码的 Viterbi译码算法,后来Omura证明Viterbi译码算法等效于在加权图中寻找最优路径问题的 一个动态规划(Dynamic Programming)解决方案,随后,Forney证明它实际上是最大似然 (ML,Maximum Likelihood)译码算法,即译码器选择输出的码字通常使接收序列的条件 概率最大化。BCJR算法是1974年提出的,它实际上是最大后验概率(MAP,Maximum A Posteriori probability)译码算法。这两种算法的最优化目标略有不同:在MAP译码算法中, 信息比特错误概率是最小的,而在ML译码算法中,码字错误概率是最小的,但两种译码算 法的性能在本质上是相同的。由于Viterbi算法实现更简单,因此在实际应用比较广泛,但 在迭代译码应用中,例如逼近Shannon限的Turbo码,常使用BCJR算法。另外,在迭代译 码应用中,还有一种Viterbi算法的变种:软输出Viterbi算法(SOVA,Soft-Output Viterbi Algorithm),它是Hagenauer和Hoeher在1989年提出的。 5.1 Viterbi算法 为了理解Viterbi译码算法,我们需要将编码器状态图按时间展开(因为状态图不能反 映出时间变化情况),即在每个时间单元用一个分隔开的状态图来表示。例如(3,1,2)非 系统前馈编码器,其生成矩阵为: G(D)=1+D1+D21+D+D2] (5.1) (a) 1 Copyright by周武旸
第五章 卷积码的译码算法 1 Copyright by 周武旸 第五章 卷积码的译码算法 卷积编码器自身具有网格结构,基于此结构我们给出两种译码算法:Viterbi 译码算法和 BCJR 译码算法。基于某种准则,这两种算法都是最优的。1967 年,Viterbi 提出了卷积码的 Viterbi 译码算法,后来 Omura 证明 Viterbi 译码算法等效于在加权图中寻找最优路径问题的 一个动态规划(Dynamic Programming)解决方案,随后,Forney 证明它实际上是最大似然 (ML,Maximum Likelihood)译码算法,即译码器选择输出的码字通常使接收序列的条件 概率最大化。BCJR 算法是 1974 年提出的,它实际上是最大后验概率(MAP,Maximum A Posteriori probability)译码算法。这两种算法的最优化目标略有不同:在 MAP 译码算法中, 信息比特错误概率是最小的,而在 ML 译码算法中,码字错误概率是最小的,但两种译码算 法的性能在本质上是相同的。由于 Viterbi 算法实现更简单,因此在实际应用比较广泛,但 在迭代译码应用中,例如逼近 Shannon 限的 Turbo 码,常使用 BCJR 算法。另外,在迭代译 码应用中,还有一种 Viterbi 算法的变种:软输出 Viterbi 算法(SOVA,Soft-Output Viterbi Algorithm),它是 Hagenauer 和 Hoeher 在 1989 年提出的。 5.1 Viterbi 算法 为了理解 Viterbi 译码算法,我们需要将编码器状态图按时间展开(因为状态图不能反 映出时间变化情况),即在每个时间单元用一个分隔开的状态图来表示。例如(3,1,2)非 系统前馈编码器,其生成矩阵为: 2 2 () 1 1 1 D D D DD =+ + ++ G (5.1) (0) v (1) u v (2) v (a)

第五章卷积码的译码算法 001 001 001 010 S 100 100 /000 So 000 /000 0000 2* /000 S 7000 000 0 2 3 6 7 时间单元一 (b) 图5.1(a)(3,1,2)编码器(b)网格图(h=5) 假定信息序列长度为h=5,则网格图包含有h十m+1=8个时间单元,用0到h十m= 7来标识,如图5.1(b)所示。假设编码器总是从全0态S,开始,又回到全0态,前=2 个时间单元对应于编码器开始从S。“启程”,最后m=2个时间单元对应于向S。“返航”。 从图中我们也可以看到,在前m个时间单元或最后m个时间单元,并不是所有状态都会出 现,但在网格图的中央部分,在每个时间单元都会包含所有状态,且在每个状态都有2=2 个分支离开和到达。离开每个状态的上面分支表示输入比特为1(即山=1,1表示第i个时 间单元),下面的分支表示输入比特为0。每个分支的输出V,由个比特组成,共有2=32 个码字,每个码字都可用网格图中的唯一路径表示,码字长度N=n(h十m)=21。例如当信 息序列为u=(11101)时,对应的码字如图5.1(b)中红线所示,v=(111,010,001, 110,100,101,011)。在一般的(n,k,v)编码器情况下,信息序列长度K*=h,离开和 进入每个状态都有2个分支,有2个不同路径通过网格图,对应着2个码字。 假设长度K*=h的信息序列u=(uo,u1…uh-)被编码成长度为N=n(h+m)的码 字V=(Vo,V1Vh+m-),在经过一个二进制输入、Q-ary输出的离散无记忆信道(DMC, Discrete memoryless Channel)后,接收序列为r=(,…ra+m-i)。也可表示为: u=(4o,4…4x-i),V=(Vo,…Vw-1),r=(,片…w-i),译码器对接收到的序列r进 行处理,得到V的估计氵。在离散无记忆信道情况下,最大似然译码器是按照最大化对数 似然函数logP(rv)作为选择ⅴ的准则。因为对于DMC, rl-)) (5.2) 两边取对数后为: 2 Copyright by周武旸
第五章 卷积码的译码算法 2 Copyright by 周武旸 0 S 2 S 3 S 000 0 1 2 3 4 5 6 7 1 S 0 S 0 S 0 S 0 S 000 0 S 0 S 0 S 000 000 000 000 000 1 S 3 S 001 3 S 3 S 001 1 S 1 S 1 S 2 S 2 S 2 S 2 S 001 111 111 111 111 111 011 011 011 011 011 100 100 100 010 010 010 010 110 110 110 110 101 101 101 101 101 时间单元 (b) 图 5.1 (a)(3,1,2)编码器 (b)网格图(h=5) 假定信息序列长度为 h=5,则网格图包含有 h+m+1=8 个时间单元,用 0 到 h+m= 7 来标识,如图 5.1(b)所示。假设编码器总是从全 0 态 S0开始,又回到全 0 态,前 m=2 个时间单元对应于编码器开始从 S0“启程”,最后 m=2 个时间单元对应于向 S0 “返航”。 从图中我们也可以看到,在前 m 个时间单元或最后 m 个时间单元,并不是所有状态都会出 现,但在网格图的中央部分,在每个时间单元都会包含所有状态,且在每个状态都有 2k =2 个分支离开和到达。离开每个状态的上面分支表示输入比特为 1(即 ui=1,i 表示第 i 个时 间单元),下面的分支表示输入比特为 0。每个分支的输出 vi由 n 个比特组成,共有 2h =32 个码字,每个码字都可用网格图中的唯一路径表示,码字长度 N=n(h+m)=21。例如当信 息序列为 u=(11101)时,对应的码字如图 5.1(b)中红线所示,v=(111,010,001, 110,100,101,011)。在一般的(n,k,v)编码器情况下,信息序列长度 K*=kh,离开和 进入每个状态都有 2k 个分支,有 * 2K 个不同路径通过网格图,对应着 * 2K 个码字。 假设长度 K kh * = 的信息序列 01 1 (, ) u uu u = h− 被编码成长度为 N nh m = + ( ) 的码 字 01 1 (, ) = h m+ − v vv v ,在经过一个二进制输入、Q-ary 输出的离散无记忆信道(DMC, Discrete memoryless Channel )后, 接 收序列为 01 1 (, ) = h m+ − r rr r 。也可表示为: 0 1 *1 (, ) K uu u u = − , 01 1 (, ) N v v = − v v , 01 1 (, ) N rr r = − r ,译码器对接收到的序列 r 进 行处理,得到 v 的估计 vˆ 。在离散无记忆信道情况下,最大似然译码器是按照最大化对数 似然函数log ( | ) P r v 作为选择 vˆ 的准则。因为对于 DMC, 1 1 0 0 (|) ( | ) ( | ) h m N l l l l l l P P Pr v + − − = = rv r v = ∏ ∏= (5.2) 两边取对数后为:

第五章卷积码的译码算法 log P(r,v,)=log P(r lv N-1 logP(rlv)=】 (5.3) 其中P(:y)是信道转移概率,当所有码字等概时,这是个最小错误概率译码准则。 对数似然函数logP(r|v),用M(r|v)表示,称为路径度量(path metric): logP(r,Iv,),称为分支度量(branch metric),用M(cv,)表示:logP(yIy)称为比特 度量(bit metric),用M(yly)表示,这样(5.3)式可写为: V-I (5.4) 如果我们只考虑前t个分支,则部分路径度量可表示为: MrI)=MGIV)=M,I) (5.5) 1-0 1-0 对于接收序列r,Viterbi算法就是通过网格图找到具有最大度量的路径,即最大似然路 径(码字)。在每个时间单元的每个状态,都增加2个分支度量到以前存储的路径度量中(加): 然后对进入每个状态的所有2个路径度量进行比较(比),选择具有最大度量的路径(选), 最后存储每个状态的幸存路径及其度量。 Viterbi算法: Stp1:在t=m时间单元开始,计算进入每个状态的单个路径的部分度量,存储每个状 态的路径(幸存)及其度量: Step 2: t←t十1,对进入每个状态的所有2个路径计算部分度量,并加上前一时间单元 的度量。对于每个状态,比较进入该状态的所有2个路径度量,选择具有最大 度量的路径,存储其度量,并删掉其他路径。 Step 3: 如果th+m,返回step2:否则,就停止。 Viterbi算法的基本计算“加、比、选”体现在step2。注:实际工程中,在每个状态存 储(在step1和step2)的是对应于幸存路径的信息序列,而不是幸存路径自身,这样当算 法结束时,就无需再通过估计码字氵来恢复信息序列ǜ。 从时间单元m到h,有2"个幸存路径,每个状态(共有2"个状态)一个。随后,幸存 路径数就会变少,因为当编码器回到全0态时,状态数就会变少。最后,在时间单元h十m, 就只有一个状态(即全0态),因此,也就只有一个幸存路径了,算法中止。 定理5.1:在Viterbi算法中最后的幸存路径是最大似然路径,即 M(r|)≥M(rlv),forv≠v (5.6) 从实现的角度看,用正整数度量来表示要比用实际的比特度量表示更方便。比特度量 M(G|y)=lo(;Iy)可用c2logP(G|y,)+c]来代替,其中c是任意实数,c2是任意 正实数。可证明,如果路径V最大化M(v)=∑MG,)=∑01oG),则 Copyright by周武肠
第五章 卷积码的译码算法 3 Copyright by 周武旸 1 1 0 0 log ( | ) log ( | ) log ( | ) h m N l l l l l l P P Pr v + − − = = rv r v = ∑ ∑= (5.3) 其中 (| ) Pr v l l 是信道转移概率,当所有码字等概时,这是个最小错误概率译码准则。 对数似然函数 log ( | ) P r v ,用 M (|) r v 表示,称为 路径度量( path metric ); log ( | ) P l l r v ,称为分支度量(branch metric),用 (| ) M l l r v 表示;log ( | ) Pr v l l 称为比特 度量(bit metric),用 (| ) Mr v l l 表示,这样(5.3)式可写为: 1 1 0 0 (|) ( | ) ( | ) h m N l l l l l l M M Mr v + − − = = rv r v = ∑ ∑= (5.4) 如果我们只考虑前 t 个分支,则部分路径度量可表示为: 1 1 0 0 (|) ( | ) ( | ) t nt l l l l l l M M Mr v − − = = rv r v = ∑ ∑= (5.5) 对于接收序列 r,Viterbi 算法就是通过网格图找到具有最大度量的路径,即最大似然路 径(码字)。在每个时间单元的每个状态,都增加 2k 个分支度量到以前存储的路径度量中(加); 然后对进入每个状态的所有 2k个路径度量进行比较(比),选择具有最大度量的路径(选), 最后存储每个状态的幸存路径及其度量。 Viterbi 算法: Step 1: 在 t=m 时间单元开始,计算进入每个状态的单个路径的部分度量,存储每个状 态的路径(幸存)及其度量; Step 2: tt+1,对进入每个状态的所有 2k 个路径计算部分度量,并加上前一时间单元 的度量。对于每个状态,比较进入该状态的所有 2k 个路径度量,选择具有最大 度量的路径,存储其度量,并删掉其他路径。 Step 3: 如果 t<h+m,返回 step 2;否则,就停止。 Viterbi 算法的基本计算“加、比、选”体现在 step 2。注:实际工程中,在每个状态存 储(在 step 1 和 step 2)的是对应于幸存路径的信息序列,而不是幸存路径自身,这样当算 法结束时,就无需再通过估计码字 vˆ 来恢复信息序列uˆ 。 从时间单元 m 到 h,有2v 个幸存路径,每个状态(共有 2v 个状态)一个。随后,幸存 路径数就会变少,因为当编码器回到全 0 态时,状态数就会变少。最后,在时间单元 h+m, 就只有一个状态(即全 0 态),因此,也就只有一个幸存路径了,算法中止。 定理 5.1:在 Viterbi 算法中最后的幸存路径 vˆ 是最大似然路径,即 M M for ( | ) ( | ), rv rv v v ˆˆ ≥ ≠ (5.6) 从实现的角度看,用正整数度量来表示要比用实际的比特度量表示更方便。比特度量 ( | ) lo g( | ) M r v Pr v l l = l l 可用c Pr v c 2 1 [log ( | ) l l + ]来代替,其中 c1 是任意实数,c2 是任意 正实数。可证明,如果路径 v 最大化 1 1 0 0 ( | ) ( | ) lo g( | ) N N l l l l M l l M r v Pr v − − = = r v = ∑ ∑= ,则
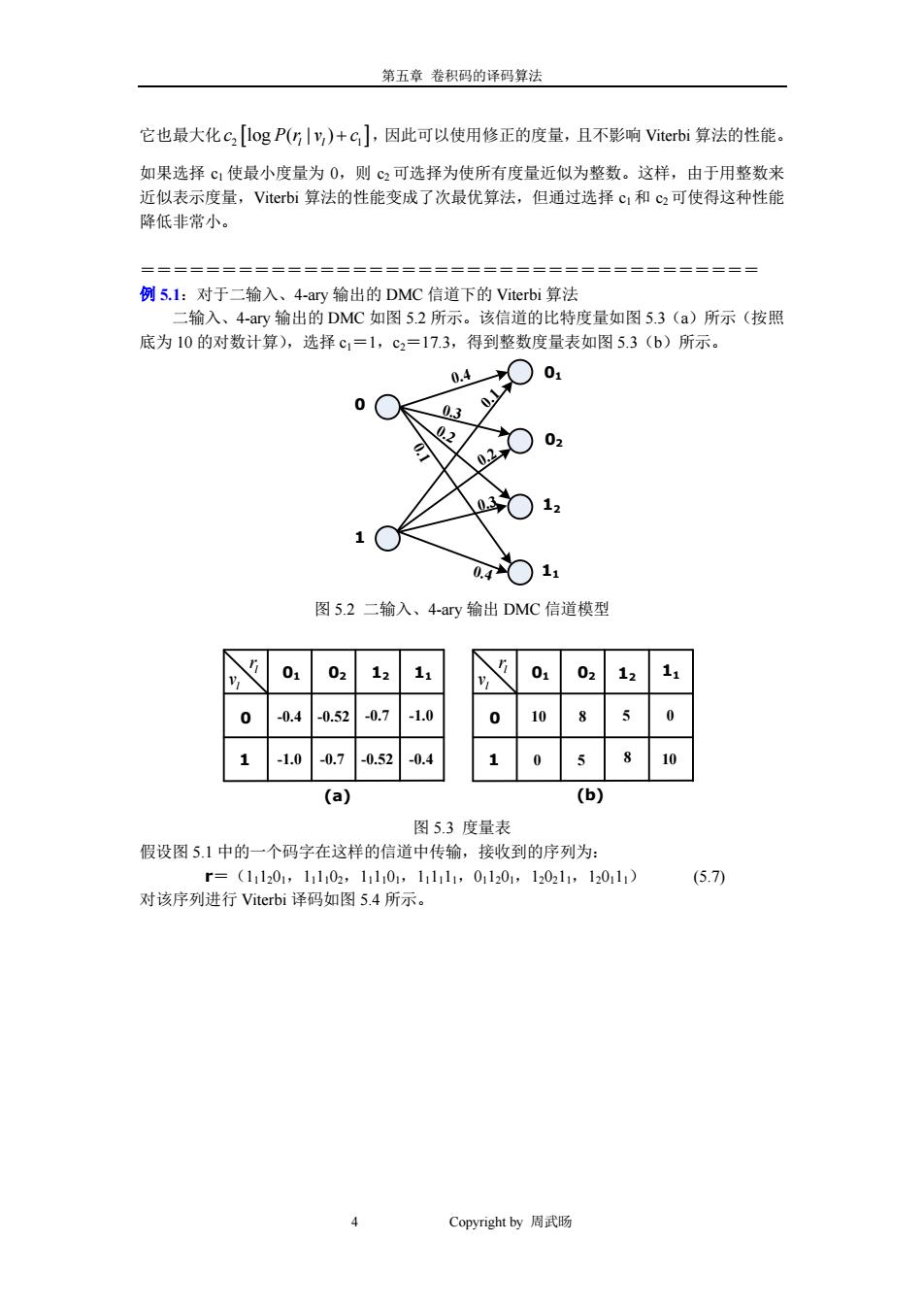
第五章卷积码的译码算法 它也最大化c2[logP(GIy,)+c],因此可以使用修正的度量,且不影响Viterbi算法的性能。 如果选择©1使最小度量为0,则c2可选择为使所有度量近似为整数。这样,由于用整数来 近似表示度量,Viterbi算法的性能变成了次最优算法,但通过选择c1和c2可使得这种性能 降低非常小。 例5.1:对于二输入、4-ary输出的DMC信道下的Viterbi算法 二输入、4-ary输出的DMC如图5.2所示。该信道的比特度量如图5.3(a)所示(按照 底为10的对数计算),选择c1=1,c2=17.3,得到整数度量表如图5.3(b)所示。 0.4 01 0 0.3 0 11 图5.2二输入、4-ary输出DMC信道模型 01 02 12 11 01 02 12 11 0 -0.4 -0.52 -0.7 -1.0 0 10 5 0 -1.0 -0.7 -0.52 -0.4 1 0 5 8 10 (a) (b) 图5.3度量表 假设图5.1中的一个码字在这样的信道中传输,接收到的序列为: r=(11l201,1102,11101,111l1,011201,120211,120111) (5.7 对该序列进行Viterbi译码如图5.4所示。 4 Copyright by周武肠
第五章 卷积码的译码算法 4 Copyright by 周武旸 它也最大化c Pr v c 2 1 [log ( | ) l l + ],因此可以使用修正的度量,且不影响 Viterbi 算法的性能。 如果选择 c1 使最小度量为 0,则 c2 可选择为使所有度量近似为整数。这样,由于用整数来 近似表示度量,Viterbi 算法的性能变成了次最优算法,但通过选择 c1 和 c2可使得这种性能 降低非常小。 ====================================== 例 5.1:对于二输入、4-ary 输出的 DMC 信道下的 Viterbi 算法 二输入、4-ary 输出的 DMC 如图 5.2 所示。该信道的比特度量如图 5.3(a)所示(按照 底为 10 的对数计算),选择 c1=1,c2=17.3,得到整数度量表如图 5.3(b)所示。 0.4 0.4 0.2 0.3 0.1 0.3 0.2 0.1 0 1 01 02 11 12 图 5.2 二输入、4-ary 输出 DMC 信道模型 lr l v 01 02 12 11 0 -0.4 1 -0.52 -0.7 -1.0 -1.0 -0.7 -0.52 -0.4 lr l v 01 02 12 11 0 10 1 8 5 0 (a) (b) 0 5 8 10 图 5.3 度量表 假设图 5.1 中的一个码字在这样的信道中传输,接收到的序列为: r=(111201,111102,111101,111111,011201,120211,120111) (5.7) 对该序列进行 Viterbi 译码如图 5.4 所示
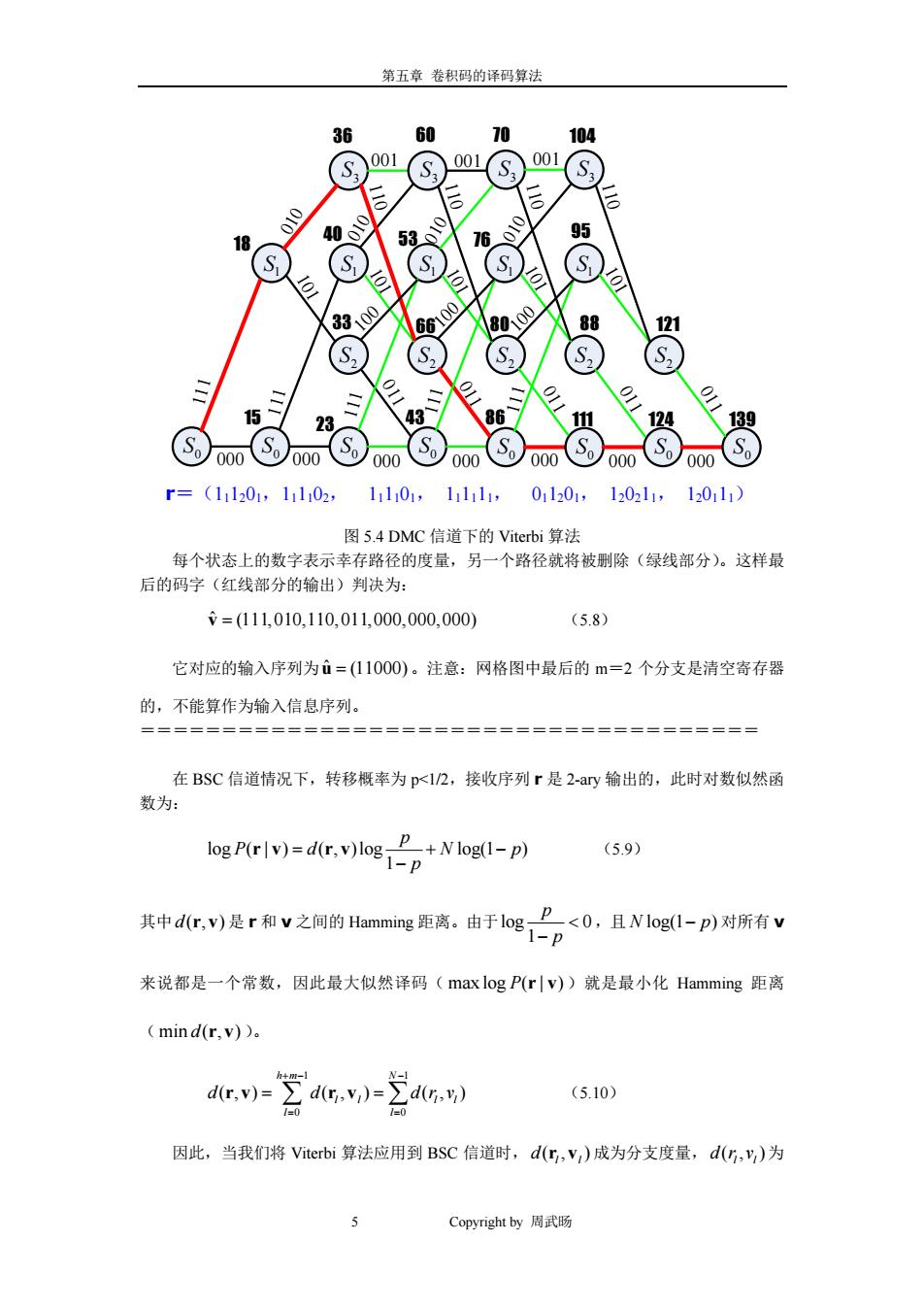
第五章卷积码的译码算法 36 60 70 104 S 001 S 001 001 010 18 4 010 5 010 76 010 95 S S S 0 3 100 6100 8000 88 121 S2 23 43 86 139 000 000 000 000 000 0 000 000 So (11201,11102, 11101,11111, 011201, 120211,1230111) 图5.4DMC信道下的Viterbi算法 每个状态上的数字表示幸存路径的度量,另一个路径就将被删除(绿线部分)。这样最 后的码字(红线部分的输出)判决为: =(111,010,110,011,000,000,000) (5.8) 它对应的输入序列为ù=(11000)。注意:网格图中最后的m=2个分支是清空寄存器 的,不能算作为输入信息序列。 在BSC信道情况下,转移概率为p<12,接收序列r是2-ay输出的,此时对数似然函 数为: log P(r v)=d(r.v)log+N log(1-p) (5.9) 其中dc,)是r和v之间的Hamming距离。由于log P<0,且NIog(1-p)对所有V 来说都是一个常数,因此最大似然译码(max log P(r|v))就是最小化Hamming距离 (mind(r,v))。 N-1 d(r,v)= (5.10) =0 1=0 因此,当我们将Viterbi算法应用到BSC信道时,d(c,V,)成为分支度量,d(,y)为 5 Copyright by周武肠
第五章 卷积码的译码算法 5 Copyright by 周武旸 0 S 2 S 3 S 000 1 S 0 S 0 S 0 S 0 S 000 0 S 0 S 0 S 000 000 000 000 000 1 S 3 S 001 3 S 3 S 001 1 S 1 S 1 S 2 S 2 S 2 S 2 S 001 111 111 111 111 111 011 011 011 011 011 100 100 100 010 010 010 010 110 110 110 110 101 101 101 101 101 r=(111201,111102, 111101, 111111, 011201, 120211, 120111) 18 36 60 70 104 40 33 15 23 43 86 111 124 139 53 66 76 80 88 95 121 图 5.4 DMC 信道下的 Viterbi 算法 每个状态上的数字表示幸存路径的度量,另一个路径就将被删除(绿线部分)。这样最 后的码字(红线部分的输出)判决为: vˆ = (111,010,110,011,000,000,000) (5.8) 它对应的输入序列为uˆ = (11000)。注意:网格图中最后的 m=2 个分支是清空寄存器 的,不能算作为输入信息序列。 ====================================== 在 BSC 信道情况下,转移概率为 p<1/2,接收序列 r 是 2-ary 输出的,此时对数似然函 数为: log ( | ) ( , )log log(1 ) 1 p P d Np p = +− − r v rv (5.9) 其中d(, ) r v 是 r 和 v 之间的 Hamming 距离。由于log 0 1 p p < − ,且 N p log(1 ) − 对所有 v 来说都是一个常数,因此最大似然译码( max log ( | ) P r v )就是最小化 Hamming 距离 ( min ( , ) d r v )。 1 1 0 0 (, ) ( , ) ( , ) h m N l l l l l l d d drv + − − = = rv r v = ∑ ∑= (5.10) 因此,当我们将 Viterbi 算法应用到 BSC 信道时, (, ) l l d r v 成为分支度量, (, ) l l drv 为