
第六章Turbo码 虽然软判决译码、级联码和编码调制技术都对信道码的设计和发 展产生了重大影响,但是其增益与Shannon理论极限始终都存在2~ 3dB的差距。因此,在Turbo码提出以前,信道截止速率Ro一直被 认为是差错控制码性能的实际极限,Shannon极限仅仅是理论上的极 限,是不可能达到的。 根据Shannon有噪信道编码定理,在信道传输速率R不超过信道 容量C的前提下,只有在码组长度无限的码集合中随机地选择编码 码字并且在接收端采用最大似然译码算法时,才能使误码率接近为 零。但是最大似然译码的复杂性随编码长度的增加而加大,当编码长 度趋于无穷大时,最大似然译码是不可能实现的。所以人们认为随机 性编译码仅仅是为证明定理存在性而引入的一种数学方法和手段,在 实际的编码构造中是不可能实现的。 在1993年于瑞士日内瓦召开的国际通信会议(1CC93)上,两位任 教于法国不列颠通信大学的教授C.Berrou、A.Glavieux和他们的缅 甸籍博士生P.thitimajshima首次提出了一种新型信道编码方案一一 Turbo码,由于它很好地应用了shannon信道编码定理中的随机性 编、译码条件,从而获得了几乎接近shannon理论极限的译码性能
第六章 Turbo 码 虽然软判决译码、级联码和编码调制技术都对信道码的设计和发 展产生了重大影响,但是其增益与 Shannon 理论极限始终都存在 2~ 3dB 的差距。因此,在 Turbo 码提出以前,信道截止速率 R0一直被 认为是差错控制码性能的实际极限,Shannon 极限仅仅是理论上的极 限,是不可能达到的。 根据 Shannon 有噪信道编码定理,在信道传输速率 R 不超过信道 容量 C 的前提下,只有在码组长度无限的码集合中随机地选择编码 码字并且在接收端采用最大似然译码算法时,才能使误码率接近为 零。但是最大似然译码的复杂性随编码长度的增加而加大,当编码长 度趋于无穷大时,最大似然译码是不可能实现的。所以人们认为随机 性编译码仅仅是为证明定理存在性而引入的一种数学方法和手段,在 实际的编码构造中是不可能实现的。 在 1993 年于瑞士日内瓦召开的国际通信会议(ICC'93)上,两位任 教于法国不列颠通信大学的教授 C.Berrou、A.Glavieux 和他们的缅 甸籍博士生 P.thitimajshima 首次提出了一种新型信道编码方案—— Turbo 码,由于它很好地应用了 shannon 信道编码定理中的随机性 编、译码条件,从而获得了几乎接近 shannon 理论极限的译码性能

Claude Berrou Dave Forney Turbo码又称并行级联卷积码(PCCC,Parallel Concatenated Convolutional Code),它巧妙地将卷积码和随机交织器结合在一起, 在实现随机编码思想的同时,通过交织器实现了由短码构造长码的方 法,并采用软输出迭代译码来逼近最大似然译码。可见,Tubo码充 分利用了Shannon信道编码定理的基本条件,因此得到了接近 Shannon极限的性能。 在介绍Turbo码的首篇论文里,发明者Berrou仅给出了Turbo 码的基本组成和迭代译码的原理,而没有严格的理论解释和证明。因 此,在Tubo码提出之初,其基本理论的研究就显得尤为重要。 J.Hagenauer首先系统地阐明了迭代译码的原理,并推导了二进制分 组码与卷积码的软输入软输出译码算法。由于在Tubo码中交织器 的出现,使其性能分析异常困难,因此S.Benedetto等人提出了均匀 交织(UI,Uniform interleaver)的概念,并利用联合界技术给出了 Turbo码的平均性能上界。D.Divsalar等人也根据卷积码的转移函 数,给出了Turbo码采用MLD时的误比特率上界。对于Turbo码 来说,标准联合界在信噪比较小时比较宽松,只有在信噪比较大时才
Turbo 码又称并行级联卷积码 (PCCC,Parallel Concatenated Convolutional Code),它巧妙地将卷积码和随机交织器结合在一起, 在实现随机编码思想的同时,通过交织器实现了由短码构造长码的方 法,并采用软输出迭代译码来逼近最大似然译码。可见,Turbo 码充 分利用了 Shannon 信道编码定理的基本条件,因此得到了接近 Shannon 极限的性能。 在介绍 Turbo 码的首篇论文里,发明者 Berrou 仅给出了 Turbo 码的基本组成和迭代译码的原理,而没有严格的理论解释和证明。因 此,在 Turbo 码提出之初,其基本理论的研究就显得尤为重要。 J.Hagenauer 首先系统地阐明了迭代译码的原理,并推导了二进制分 组码与卷积码的软输入软输出译码算法。由于在 Turbo 码中交织器 的出现,使其性能分析异常困难,因此 S.Benedetto 等人提出了均匀 交织(UI,Uniform interleaver)的概念,并利用联合界技术给出了 Turbo 码的平均性能上界。D.Divsalar 等人也根据卷积码的转移函 数,给出了 Turbo 码采用 MLD 时的误比特率上界。对于 Turbo 码 来说,标准联合界在信噪比较小时比较宽松,只有在信噪比较大时才 Claude Berrou Dave Forney

能实现对Turbo码性能的度量。因此,T.M.Duman、L.Sason和 D.Divsalar等人在Gallager限等已有性能界技术的基础上进行改 进.扩展了Turbo码性能界的紧致范围。D.Divsalar等人还根据递归 系统卷积码的特点提出了有效自由距离的概念,并说明在设计Tubo 码时应该使码字有效自由距离尽可能大。L.C.Perez等人从距离谱的 角度对Turbo码的性能进行了分析,证明可以通过增加交织长度或 采用本原反馈多项式增加分量码的自由距离来提高Tbo码的性能。 他们还证明了Turbo码虽然自由距离比较小,但其低重量码字的数 目较少,从而解释了低信噪比条件下Tubo码性能优异的原因,并 提出了交织器增益的概念。S.Dolinar的研究表明,Turbo码的最小 距离码字主要由重量为2的输入信息序列生成,是形成错误平台的主 要原因。为提高高信噪比条件下Tubo码的性能,就必须提高低重 输入信息序列的输出码重。J.Seghers系统地分析了Turbo码的距离 特性。由于交织器的存在,无法给出Tubo码自由距离的严格数学 表示,相应地也出现了许多分析和计算Tubo码最小距离、重量分 布和性能上限的方法。A.Ambroze还构造了Turbo码的树图,用来 作为计算码字距离谱的工具。此外,R.Tanner、E.Offer和K.Engdahl 分别从代数和统计的角度对Turbo码进行了分析。考虑到Turbo码 的延时问题,E.Hal等人提出了面向流的Turbo码。也可以用其他 系统模型采描述Turbo码及其迭代译码过程:T.Richardson把Turbo 码作为一个动力学系统进行描述;A.Khandani则把Turbo码考虑成 一个周期性的线性系统;J.Laertyy,X.Ge和R.Kschischang描述了
能实现对 Turbo 码性能的度量。因此,T.M.Duman、I.Sason 和 D.Divsalar 等人在 Gallager 限等已有性能界技术的基础上进行改 进.扩展了 Turbo 码性能界的紧致范围。D.Divsalar 等人还根据递归 系统卷积码的特点提出了有效自由距离的概念,并说明在设计 Turbo 码时应该使码字有效自由距离尽可能大。L.C.Perez 等人从距离谱的 角度对 Turbo 码的性能进行了分析,证明可以通过增加交织长度或 采用本原反馈多项式增加分量码的自由距离来提高 Turbo 码的性能。 他们还证明了 Turbo 码虽然自由距离比较小,但其低重量码字的数 目较少,从而解释了低信噪比条件下 Turbo 码性能优异的原因,并 提出了交织器增益的概念。S.Dolinar 的研究表明,Turbo 码的最小 距离码字主要由重量为 2 的输入信息序列生成,是形成错误平台的主 要原因。为提高高信噪比条件下 Turbo 码的性能,就必须提高低重 输入信息序列的输出码重。J.Seghers 系统地分析了 Turbo 码的距离 特性。由于交织器的存在,无法给出 Turbo 码自由距离的严格数学 表示,相应地也出现了许多分析和计算 Turbo 码最小距离、重量分 布和性能上限的方法。A.Ambroze 还构造了 Turbo 码的树图,用来 作为计算码字距离谱的工具。此外,R. Tanner、E.Offer 和 K.Engdahl 分别从代数和统计的角度对 Turbo 码进行了分析。考虑到 Turbo 码 的延时问题,E. Hall 等人提出了面向流的 Turbo 码。也可以用其他 系统模型采描述 Turbo 码及其迭代译码过程:T.Richardson 把 Turbo 码作为一个动力学系统进行描述;A. Khandani 则把 Turbo 码考虑成 一个周期性的线性系统;J.Laertyy, X.Ge 和 F. Kschischang 描述了
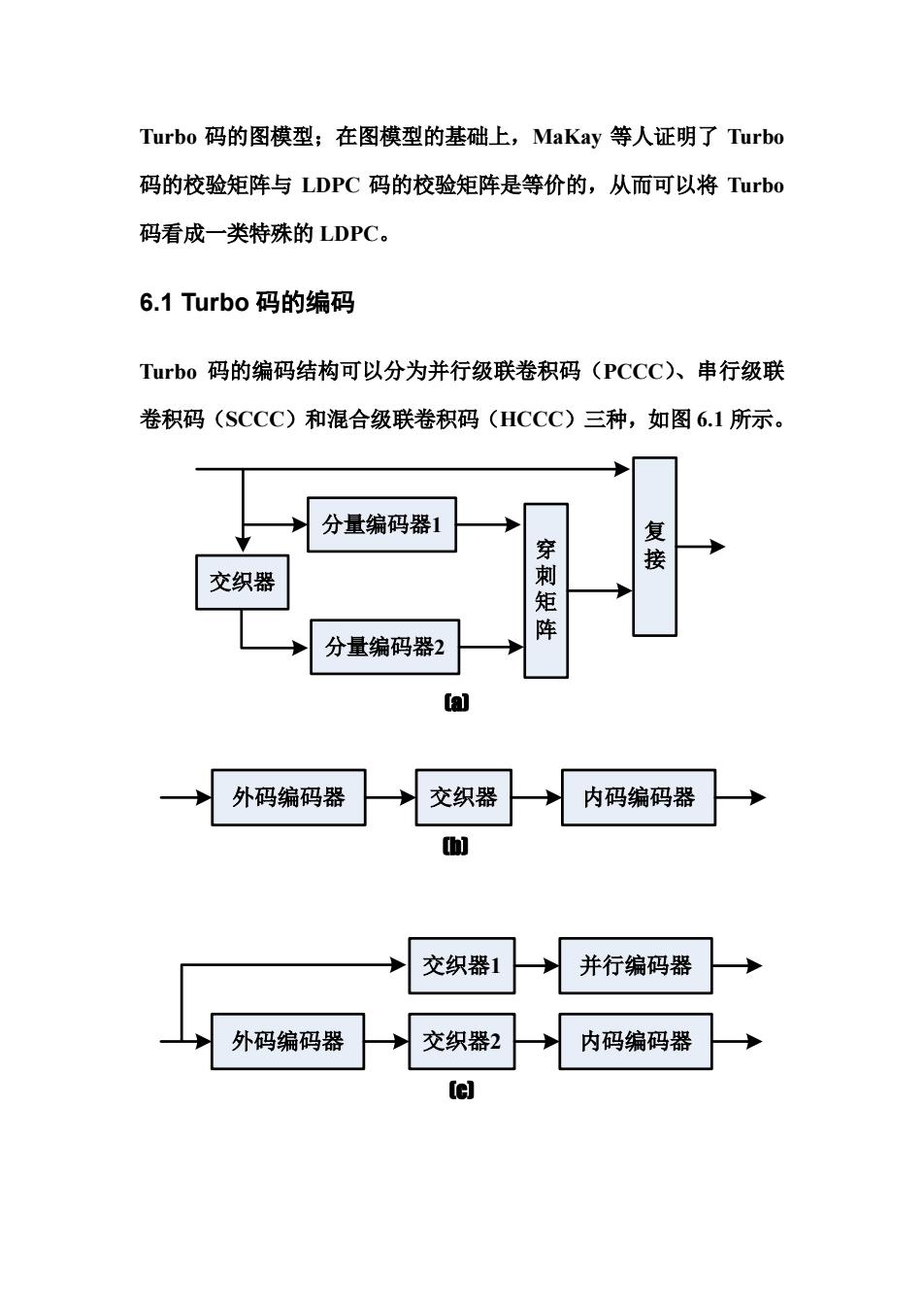
Turbo码的图模型;在图模型的基础上,MaKay等人证明了Turbo 码的校验矩阵与LDPC码的校验矩阵是等价的,从而可以将Turbo 码看成一类特殊的LDPC。 6.1 Turbo码的编码 Tubo码的编码结构可以分为并行级联卷积码(PCCC)、串行级联 卷积码(SCCC)和混合级联卷积码(HCCC)三种,如图6.1所示。 分量编码器1 接 交织器 穿刺矩阵 分量编码器2 外码编码器 交织器 内码编码器 ] 交织器1 并行编码器 外码编码器 交织器2 内码编码器 te]
Turbo 码的图模型;在图模型的基础上,MaKay 等人证明了 Turbo 码的校验矩阵与 LDPC 码的校验矩阵是等价的,从而可以将 Turbo 码看成一类特殊的 LDPC。 6.1 Turbo 码的编码 Turbo 码的编码结构可以分为并行级联卷积码(PCCC)、串行级联 卷积码(SCCC)和混合级联卷积码(HCCC)三种,如图 6.1 所示。 分量编码器1 分量编码器2 交织器 复 穿 接 刺 矩 阵 (a) 外码编码器 交织器 内码编码器 (b) 外码编码器 交织器2 内码编码器 交织器1 并行编码器 (c)

外码编码器 交织器1 内码编码器1 交织器2 内码编码器2 图6.1 Turbo码的几种编码结构(a)PCCC(b)SCCC(c)HCCC-I (d)HCCC-IⅡ 1993年,C.Berrou提出的Turbo码就是PCCC结构,主要由分 量编码器、交织器、穿刺矩阵和复接器组成。分量码一般选择为递归 系统卷积(RSC)码,当然也可以选择分组码、非递归卷积(NRC) 码以及非系统卷积(NSC)码。通常两个分量码采用相同的生成矩阵 (也可不同)。若两个分量码的码率分别为R1和R2,则Turbo码的 码率为: R= RR R+R-RR (6.1) 在AWGN信道上对PCCC的性能仿真证明,当BER随SNR的 增加下降到一定程度时,就会出现下降缓慢甚至不再降低的情况,一 般称为误码平台(error floor)。为解决这个问题,l996年,S.Benedetto 提出了串行级联卷积码(SCCC)的概念,它综合了Forney串行级 联码(RS码+卷积码)和Turbo码(PCCC)的特点,在适当的信 噪比范围内,通过迭代译码可以达到非常优异的译码性能。Benedetto
外码编码器 交织器1 交织器2 内码编码器1 (d) 内码编码器2 图 6.1 Turbo 码的几种编码结构(a)PCCC(b)SCCC(c)HCCC-I (d)HCCC-II 1993 年,C.Berrou 提出的 Turbo 码就是 PCCC 结构,主要由分 量编码器、交织器、穿刺矩阵和复接器组成。分量码一般选择为递归 系统卷积(RSC)码,当然也可以选择分组码、非递归卷积(NRC) 码以及非系统卷积(NSC)码。通常两个分量码采用相同的生成矩阵 (也可不同)。若两个分量码的码率分别为 R1和 R2,则 Turbo 码的 码率为: 1 2 1 2 12 R R R R R RR = + − (6.1) 在 AWGN 信道上对 PCCC 的性能仿真证明,当 BER 随 SNR 的 增加下降到一定程度时,就会出现下降缓慢甚至不再降低的情况,一 般称为误码平台(error floor)。为解决这个问题,1996 年,S.Benedetto 提出了串行级联卷积码(SCCC)的概念,它综合了 Forney 串行级 联码(RS 码+卷积码)和 Turbo 码(PCCC)的特点,在适当的信 噪比范围内,通过迭代译码可以达到非常优异的译码性能。Benedetto