
例2如图所示,用质量为m,的铁锤把质量为m的钉 子敲入木板。设木板对钉子的阻力与钉子进入木板的 深度成正比。在铁锤敲打第一次时,能够把钉子敲入 1cm深,若铁锤第二次敲钉子的速度情况与第一次完 全相同,问第二次能把钉子敲入多深? 解:设铁锤敲打钉子前的 速度为o,敲打后两 者的共同速度为v。 mvo (mo m)v mvo mo m
例2 如图所示,用质量为m0 的铁锤把质量为m 的钉 子敲入木板。设木板对钉子的阻力与钉子进入木板的 深度成正比。在铁锤敲打第一次时,能够把钉子敲入 1cm深,若铁锤第二次敲钉子的速度情况与第一次完 全相同,问第二次能把钉子敲入多深? 解:设铁锤敲打钉子前的 速度为v0,敲打后两 者的共同速度为v。 m0 v0 = (m0 + m)v m m m + = 0 0 0 v v x O 1 s 2 s

铁锤第一次敲打时,克服阻力做功,设钉子所受阻 力大小为: F:=-kx .'m>>m,.U≈Vo 由动能定理,有: m-d=- 设铁锤第二次敲打时能敲入的深度为△S,则有 0-m=-kd=[*ar-
铁锤第一次敲打时,克服阻力做功,设钉子所受阻 力大小为: F = −kx f 由动能定理, 有: 2 1 0 2 0 2 1 d 2 1 0 1 m k x x k s s − = − = − v v v0 , m0 m + − = − s s s m k x x 1 1 d 2 1 0 2 v0 设铁锤第二次敲打时能敲入的深度为ΔS ,则有 = − + − 2 1 2 1 2 1 ( ) 2 1 k s s k s

(S+△s)2=2s1 化简后 s,As v2s; 第二次能敲入的深度为: △s=V2s-s=(2-1)×1cm=0.41cm
2 1 2 (s1 + s) = 2s 1 2 1 化简后 s + s = s 第二次能敲入的深度为: s = 2s1 − s1 = ( 2 −1)1cm = 0.41cm

2-4-3保守力与非保守力 势能 (1)重力的功 初始位置 a(Xa>Ya>Za) 末了位置 b(x6,y6,26) m.=心Fdr =广-mgk.di+d+d正) =-mg止=mg(e。-)
2-4-3 保守力与非保守力 势能 (1)重力的功 b z a z x y z O a b r mg ( , , ) a a a 初始位置 a x y z ( , , ) b b b 末了位置 b x y z = b a ab W F r d mgk ( xi yj zk ) b a = − d + d + d ( ) a b b a = − mg z = mg z − z d
重力做功仅取决于质点的始、未位置2和z6, 与质点经过的具体路径无关。 (2)万有引力做功 设质量为M的质点固 定,另一质量为m的质点 dr 在M的引力场中从a点运 动到b点。 +d F=-Ge, 2 mo e,·dr=d cosa=dr
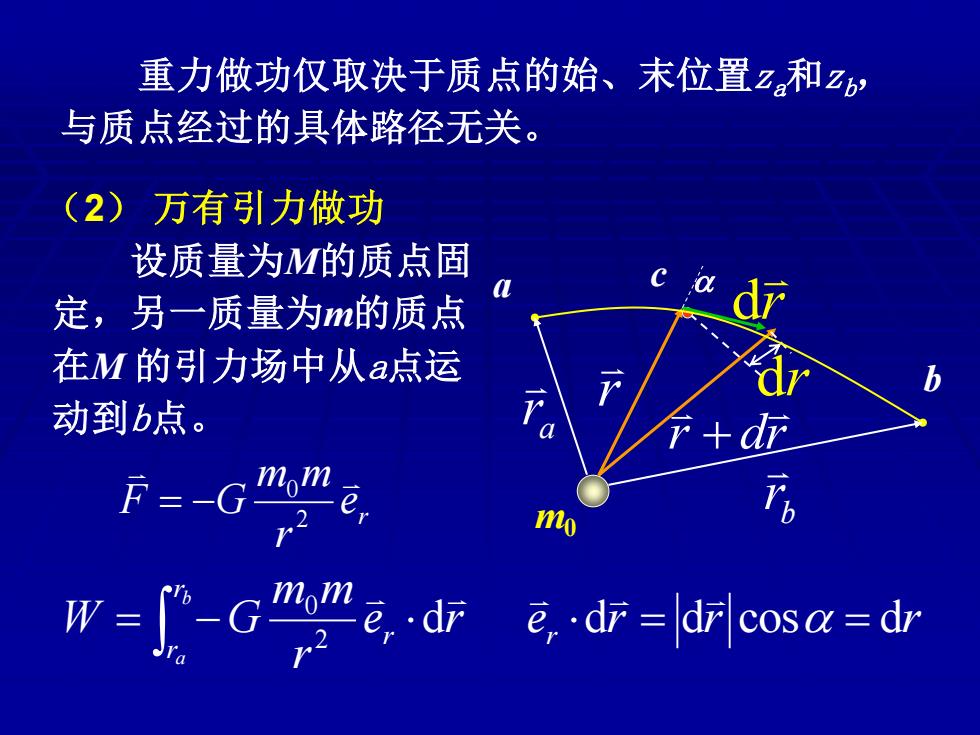
重力做功仅取决于质点的始、末位置za和zb, 与质点经过的具体路径无关。 (2) 万有引力做功 设质量为M的质点固 定,另一质量为m的质点 在M 的引力场中从a点运 动到b点。 r e r m m F G 2 0 = − = − b a r r r e r r m m W G d 2 0 e r r r r d = d cos = d r r dr + r d c dr m0 a b a r b r