
1-2求解运动学问题举例 质点运动学两类基本问题 一由质点的运动方程可以求得质点在任一时 刻的位矢、速度和加速度; 二已知质点的加速度以及初始速度和初始位 置,可求质点速度及其运动方程. 求导 求导 r(t) (t) a(t) 积分 积分
5 1 – 1–简谐运动 2 求解运动学问题举例 简谐运动的振幅 周期 频率和相位 a(t) r(t) 求导 求导 积分 积分 v( )t 质点运动学两类基本问题 一 由质点的运动方程可以求得质点在任一时 刻的位矢、速度和加速度; 二 已知质点的加速度以及初始速度和初始位 置,可求质点速度及其运动方程

1-2求解运动学问题举例 例1斜抛运动 射击 当子弹从枪口射出时,椰子刚好从树上由静止 自由下落。试说明为什么子弹总可以射中椰子?
5 1 – 1–简谐运动 2 求解运动学问题举例 简谐运动的振幅 周期 频率和相位 例1 斜抛运动 当子弹从枪口射出时,椰子刚好从树上由静止 自由下落. 试说明为什么子弹总可以射中椰子 ?
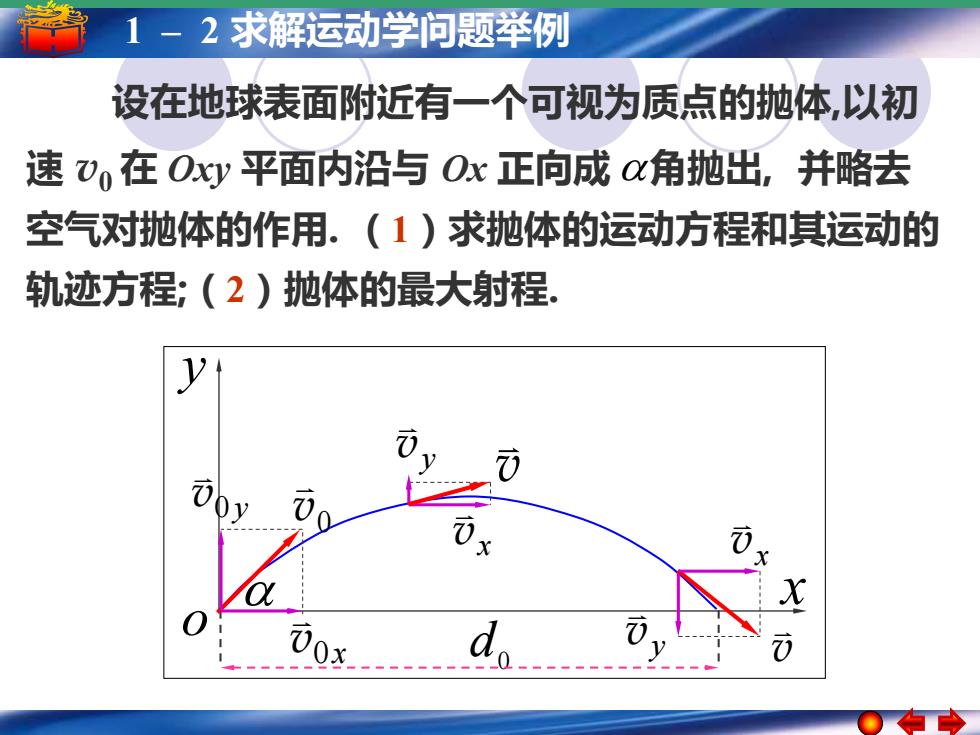
1-2求解运动学问题举例 设在地球表面附近有一个可视为质点的抛体,以初 速V,在Oxy平面内沿与Ox正向成x角抛出,并略去 空气对抛体的作用.(1)求抛体的运动方程和其运动的 轨迹方程;(2)抛体的最大射程. 7)
5 1 – 1–简谐运动 2 求解运动学问题举例 简谐运动的振幅 周期 频率和相位 x y o x v y v v 0 d 0 v 0x v v0 y 设在地球表面附近有一个可视为质点的抛体,以初 速 v0 在 Oxy 平面内沿与 Ox 正向成 角抛出, 并略去 空气对抛体的作用. (1)求抛体的运动方程和其运动的 轨迹方程;(2)抛体的最大射程. x v y v v

1-2求解运动学问题举例 已知:i0,=0,a=g Vox =v0 cosa V0y vo sin a do 解(1) a- =8=-8 dt dr )= 0+gt do di F(t)=Bot+gt2 2 消去方程中的参数t得轨迹 ∫x=0c0sa,t 8 y=xtana- y=vosina.t- 2v cos2a
5 1 – 1–简谐运动 2 求解运动学问题举例 简谐运动的振幅 周期 频率和相位 g gj t a = = = − d dv gt t r = = 0 + d d v v 2 0 2 1 t gt r(t) = v + 2 2 1 gt t v0 r x y o 0 d 已知: v0 , , 0 0 r = a g = x = cos t v0 2 0 2 1 y = v sin t − gt v0x = v0 cos v0y = v0 sin 解 (1) 2 2 2 0 2 cos tan x g y x v = − 消去方程中的参数 t 得轨迹
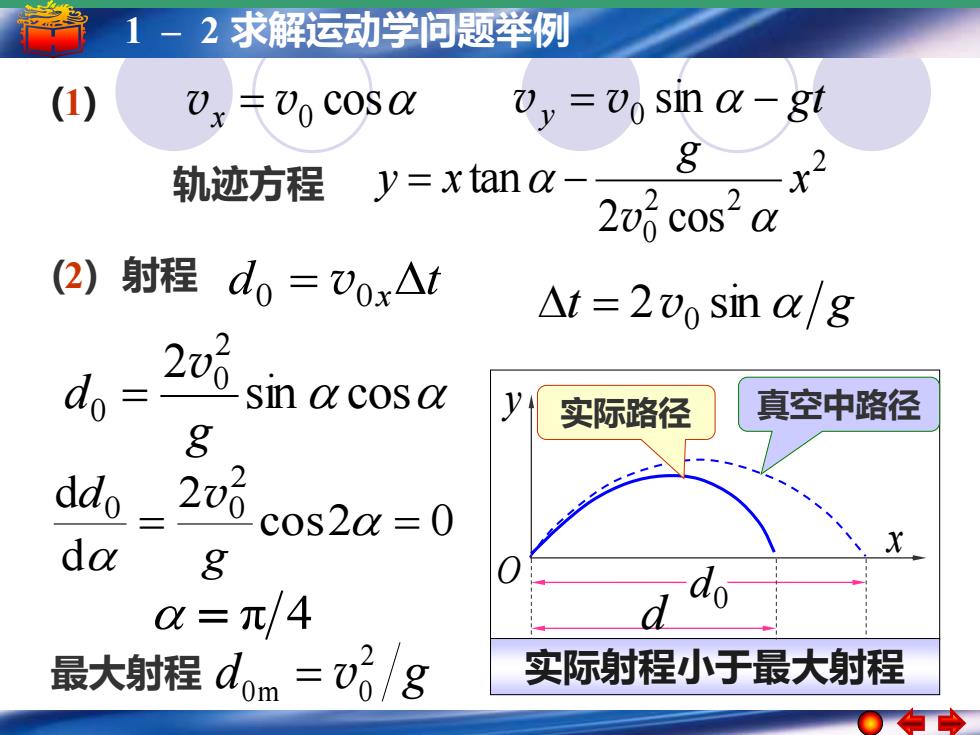
1-2求解运动学问题举例 (1) v,=vo cosa 7y =v0sma-gt 8 轨迹方程y=xtan a 2v cos2 a (2) 射程d0=Vox△t △t=2 0 sin a/g 2 2 do sin a cos a y 实际路径 真空中路径 g ddo 206 0S20=0 da 8 c=π/4 最大射程dom 0 实际射程小于最大射程
5 1 – 1–简谐运动 2 求解运动学问题举例 简谐运动的振幅 周期 频率和相位 x y O 0 d 实际射程小于最大射程 = π 4 d d g 2 0m 0 最大射程 = v cos2 0 2 d d 2 0 0 = = g d v sin cos 2 2 0 0 g d v = 2 2 2 0 2 cos tan x g y x v 轨迹方程 = − vx = v0 cos gt (1) vy = v0 sin − 实际路径 真空中路径 t = 2v0 sin g (2) 射程 d t 0 = v0x