
四、平均指标(4课时) (一)概念 1、涵义:又称统计平均数,用以反映社会经济现象 总体各单位某一数量标志在一定时间,地点条件 下所达到的一般水平。 2、特点:把总体各单位标志值的差异抽象化了,它 可能与各单位所有标志值都不相等,但作为代表 值来反映这些标志值的一般水平。 3、种类:数值平均数一一根据总体所有标志值来计 算 位置平均数一—根据总体标志值的位置来 判断,确定。 4、作用:反映总体各单位变量分布的集中趋势:比 较同类现象在不同单位的发展水平,用来说明生 产水平,经济效益或工作质量:分析现象之间的 依存关系 (二)平均指标的计算 1.算术平均数:总体标志总量除以总体单位总量。 1)简单算术平均数:适合于总体单位数较少的情况下,将每 一个标志值一一加总得到的标志总量除以单位总量求出 的平均指标。 例题:设五名学生的统计学分数分别为:80708288 65, 求其平均数
四、平均指标(4 课时) (一)概念 1、涵义:又称统计平均数,用以反映社会经济现象 总体各单位某一数量标志在一定时间,地点条件 下所达到的一般水平。 2、特点:把总体各单位标志值的差异抽象化了,它 可能与各单位所有标志值都不相等,但作为代表 值来反映这些标志值的一般水平。 3、种类:数值平均数——根据总体所有标志值来计 算 位置平均数——根据总体标志值的位置来 判断,确定。 4、作用:反映总体各单位变量分布的集中趋势;比 较同类现象在不同单位的发展水平,用来说明生 产水平,经济效益或工作质量;分析现象之间的 依存关系。 (二)平均指标的计算 1. 算术平均数:总体标志总量除以总体单位总量。 1)简单算术平均数:适合于总体单位数较少的情况下,将每 一个标志值一一加总得到的标志总量除以单位总量求出 的平均指标。 例题:设五名学生的统计学分数分别为:80 70 82 88 65, 求其平均数

解:平均分数=(总分数/人数)=(80+70+82+88+65)/5=77 x=(Σx/n) 在此例中,单位数较少,且每一个标志值仅出现一次,如果 在一个总体中,有些标志值重复出现,如某一个车间15个人, 每一个人看机器的台数分别是:223334444 555556 问:平均每人看几台机器 按照统计整理的要求,我们可以对上述资料进行分组 台数(x)人数(f) 2 3 4 4 5 合计15 解:每人平均看的机器台数=总台数/人数 =(2+2+3+3+3+4+4+4+4+5+5+5+5+5+6)/15 =(2*2+3*3+4*4+5*5+6*1)/(2+3+4+5+1) =4 由此,可以引出加权算术平均数的内容 x=(Σxf/Σf) 该计算公式说明决定平均数有两个因素:一是总体各单位 标志值(x),另一个是各个标志值的次数f∑f,即:x=Σx*(f/ Σf)
解:平均分数=(总分数/人数)=(80+70+82+88+65)/5=77 x =(Σx/n) 在此例中,单位数较少,且每一个标志值仅出现一次,如果 在一个总体中,有些标志值重复出现,如某一个车间 15 个人, 每一个人看机器的台数分别是:2 2 3 3 3 4 4 4 4 5 5 5 5 5 6 问:平均每人看几台机器? 按照统计整理的要求,我们可以对上述资料进行分组 台数(x) 人数(f) 2 3 4 5 6 2 3 4 5 1 合计 15 解:每人平均看的机器台数=总台数/人数 =(2+2+3+3+3+4+4+4+4+5+5+5+5+5+6)/15 =(2*2+3*3+4*4+5*5+6*1)/(2+3+4+5+1) =4 由此,可以引出加权算术平均数的内容 x =(Σxf/Σf) 该计算公式说明决定平均数有两个因素:一是总体各单位 标志值(x),另一个是各个标志值的次数 f/Σf,即:x=Σx*(f/ Σf)

2)加权算术平均数:加权平均数是在分配数列的条件下计算的, 它必须首先求出每组的总量,并加总取得总体的标志总量,然后 除以总体单位总数 例题:某工地起重机起重量如下表,求平均起重量 起重量(x) 台数(f) xf F/Σf 40 40 10% 2 50 20% 10 30 30% 5 4 20 40% 合计 10 140 100 X=(Σxf/Σf)=140/10=14吨或者 X=Σ(x*f/Σf)=40*10%+25*20%+10*30%+5*40%=14 加权算术平均数等于简单算术平均数的条件是:各组权数相等, 用加权算术平均数来求某一总体平均数是在数列当中进行的,分 成两种情况 1)单项式分组:直接用分组的变量值乘以次数,求得xf并 且进行累计求得 Σxf,然后除以总体单位总量指标 2)组距式分组:首先求各组的组中值作为该组变量值的代表 数x,然后再 和次数相乘并汇总,求得Σx,再除以总体单位数。 计算加权算术平均数应注意的问题:关于权数的选择,一般来讲, 在分配数列条件下,次数就是权数,但是也有次数是不合适的权
2)加权算术平均数:加权平均数是在分配数列的条件下计算的, 它必须首先求出每组的总量,并加总取得总体的标志总量,然后 除以总体单位总数. 例题:某工地起重机起重量如下表,求平均起重量 起重量(x) 台数(f) xf F/Σf 40 25 10 5 1 2 3 4 40 50 30 20 10% 20% 30% 40% 合计 10 140 100 X =(Σxf/Σf)=140/10=14 吨 或者 X =Σ(x*f/Σf)=40*10%+25*20%+10*30%+5*40%=14 加权算术平均数等于简单算术平均数的条件是:各组权数相等, 用加权算术平均数来求某一总体平均数是在数列当中进行的,分 成两种情况: 1) 单项式分组:直接用分组的变量值乘以次数,求得 xf 并 且进行累计求得 Σxf,然后除以总体单位总量指标 2) 组距式分组:首先求各组的组中值作为该组变量值的代表 数 x,然后再 和次数相乘并汇总,求得Σxf,再除以总体单位数。 计算加权算术平均数应注意的问题:关于权数的选择,一般来讲, 在分配数列条件下,次数就是权数,但是也有次数是不合适的权
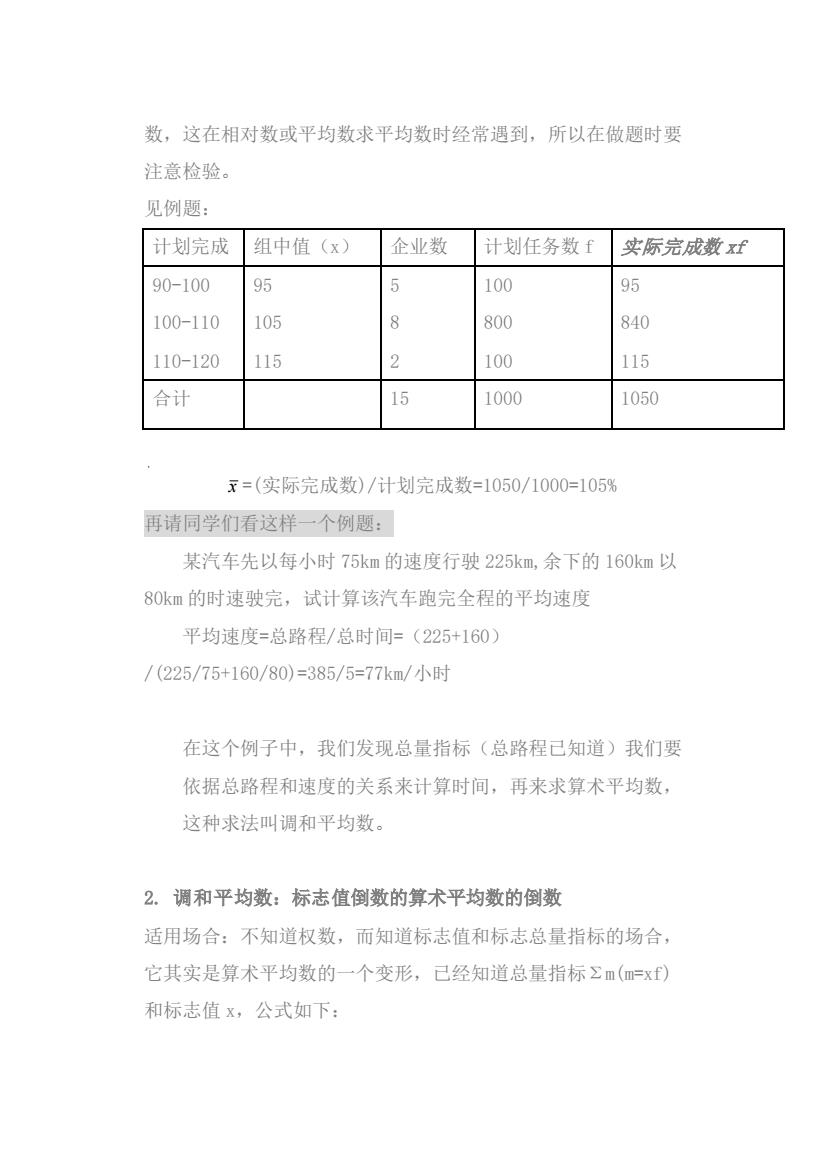
数,这在相对数或平均数求平均数时经常遇到,所以在做题时要 注意检验。 见例题: 计划完成组中值(x) 企业数 计划任务数f 实际完成数xf 90-100 95 100 95 100-110 105 800 840 110-120 115 100 115 合计 15 1000 1050 x=(实际完成数)/计划完成数=1050/1000=105% 再请同学们看这样一个例题: 某汽车先以每小时75km的速度行驶225水m,余下的160km以 80km的时速驶完,试计算该汽车跑完全程的平均速度 平均速度=总路程/总时间=(225+160) /(225/75+160/80)=385/5=77km/小时 在这个例子中,我们发现总量指标(总路程已知道)我们要 依据总路程和速度的关系来计算时间,再来求算术平均数, 这种求法叫调和平均数。 2.调和平均数:标志值倒数的算术平均数的倒数 适用场合:不知道权数,而知道标志值和标志总量指标的场合, 它其实是算术平均数的一个变形,已经知道总量指标Σm(m=x) 和标志值x,公式如下:
数,这在相对数或平均数求平均数时经常遇到,所以在做题时要 注意检验。 见例题: 计划完成 组中值(x) 企业数 计划任务数 f 实际完成数 xf 90-100 100-110 110-120 95 105 115 5 8 2 100 800 100 95 840 115 合计 15 1000 1050 x =(实际完成数)/计划完成数=1050/1000=105% 再请同学们看这样一个例题: 某汽车先以每小时 75km 的速度行驶 225km,余下的 160km 以 80km 的时速驶完,试计算该汽车跑完全程的平均速度 平均速度=总路程/总时间=(225+160) /(225/75+160/80)=385/5=77km/小时 在这个例子中,我们发现总量指标(总路程已知道)我们要 依据总路程和速度的关系来计算时间,再来求算术平均数, 这种求法叫调和平均数。 2. 调和平均数:标志值倒数的算术平均数的倒数 适用场合:不知道权数,而知道标志值和标志总量指标的场合, 它其实是算术平均数的一个变形,已经知道总量指标Σm(m=xf) 和标志值 x,公式如下:

灭=∑xf/∑f=Σm/(Σm/f) 3.众数和中位数(位置平均数) 关于众数和中位数的概念,同学们从这样几个方面来掌握,会在 所给的资料中判断出众数和中位数的那个标志值,简单掌握中位 数和众数的近似值判断 1)众数现象总体中最普遍的那个标志值。在单项式分组 中,次数最多所对应的标志值就是众数:在组距式分组中, 众数组是指该组标志值次数最多的组,近似值的确定公式 如下: mo=10+d o*[(f o-f)/(f o-f o (fo+fmo) 2)中位数:把现象总体中的各单位标志值按大小顺序排列, 处于数列中点位置的标志值。 未经分组的情况,中位数的确定为:先将各单位按标志值大 小顺序排列,若总体单位数为奇数,则处于(+1)/2位置的标 志值是中位数:若总体单位数为偶数,则中位数处于 n/2,(n/2)+1之间,中位数为达到这两个标志值的简单算术平均 数分组时,中位数近似值的确定公式为: m=lm+d*[(∑f/2-s-)]/f
X =Σxf/Σf=Σm/(Σm/f) 3. 众数和中位数(位置平均数) 关于众数和中位数的概念,同学们从这样几个方面来掌握,会在 所给的资料中判断出众数和中位数的那个标志值,简单掌握中位 数和众数的近似值判断 1)众数 现象总体中最普遍的那个标志值。在单项式分组 中,次数最多所对应的标志值就是众数;在组距式分组中, 众数组是指该组标志值次数最多的组,近似值的确定公式 如下: m0 =lm0+dm0*[(fm0-fm0-1)/(fm0-fm0+1)(fm0+fm0+1)] 2)中位数:把现象总体中的各单位标志值按大小顺序排列, 处于数列中点位置的标志值。 未经分组的情况,中位数的确定为:先将各单位按标志值大 小顺序排列,若总体单位数为奇数,则处于(n+1)/2 位置的标 志值是中位数;若总体单位数 n 为偶数,则中位数处于 n/2,(n/2)+1 之间,中位数为达到这两个标志值的简单算术平均 数分组时,中位数近似值的确定公式为: me=lme+dme*[(Σf/2-sme-1)]/fme