
毯业大学 物理化学讲稿 第十三章表面物理化学 (6学时) 物理化学教研室
物理化学讲稿 第十三章 表面物理化学 (6 学时) 物理化学教研室
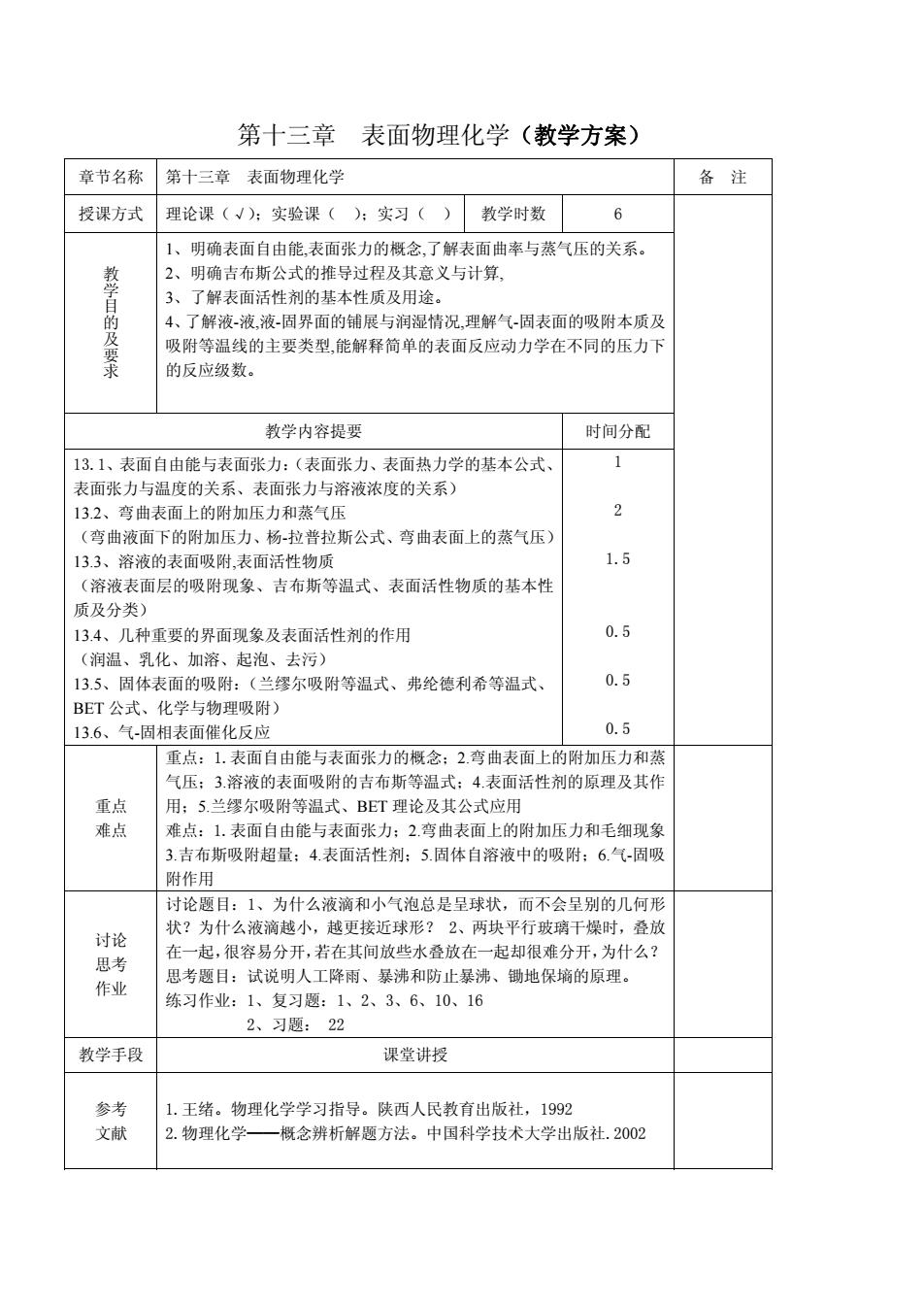
第十三章 表面物理化学(教学方案) 章节名称 第十三章 表面物理化学 备注 授课方式 理论课(√):实验课():实习( 教学时数 6 1、明确表面自由能,表面张力的概念,了解表面曲率与蒸气压的关系。 2、 明确吉布斯公式的推导过程及其意义与计算, 3、了解表面活性剂的基本性质及用途。 4、了解液-液,液-固界面的铺展与润湿情况,理解气-固表面的吸附本质及 及要求 吸附等温线的主要类型,能解释简单的表面反应动力学在不同的压力下 的反应级数。 教学内容提要 时间分配 13.1、表面自由能与表面张力:(表面张力、表面热力学的基本公式、 1 表面张力与温度的关系、表面张力与溶液浓度的关系) 13.2、弯曲表面上的附加压力和蒸气压 2 (弯曲液面下的附加压力、杨-拉普拉斯公式、弯曲表面上的蒸气压) 13.3、溶液的表面吸附,表面活性物质 1.5 (溶液表面层的吸附现象、吉布斯等温式、表面活性物质的基本性 质及分类) 13.4、几种重要的界面现象及表面活性剂的作用 0.5 (润温、乳化、加溶、起泡、去污) 13.5、固体表面的吸附:(兰缪尔吸附等温式、弗纶德利希等温式、 0.5 BET公式、化学与物理吸附) 13.6、气-固相表面催化反应 0.5 重点:1.表面自由能与表面张力的概念:2.弯曲表面上的附加压力和蒸 气压:3.溶液的表面吸附的吉布斯等温式:4.表面活性剂的原理及其作 重点 用;5.兰缪尔吸附等温式、BET理论及其公式应用 难点 难点:1.表面自由能与表面张力:2弯曲表面上的附加压力和毛细现象 3.吉布斯吸附超量:4.表面活性剂;5.固体自溶液中的吸附:6.气-固吸 附作用 讨论题目:1、为什么液滴和小气泡总是呈球状,而不会呈别的几何形 状?为什么液滴越小,越更接近球形?2、两块平行玻璃干燥时,叠放 讨论 在一起,很容易分开,若在其间放些水叠放在一起却很难分开,为什么? 思考 思考题目:试说明人工降雨、暴沸和防止暴沸、锄地保墒的原理。 作业 练习作业:1、复习题:1、2、3、6、10、16 2、习题:22 教学手段 课堂讲授 参考 1.王绪。物理化学学习指导。陕西人民教育出版社,1992 文献 2.物理化学一概念辨析解题方法。中国科学技术大学出版社.2002
第十三章 表面物理化学(教学方案) 章节名称 第十三章 表面物理化学 备 注 授课方式 理论课(√);实验课( );实习( ) 教学时数 6 教学目的及要求 1、明确表面自由能,表面张力的概念,了解表面曲率与蒸气压的关系。 2、明确吉布斯公式的推导过程及其意义与计算, 3、了解表面活性剂的基本性质及用途。 4、了解液-液,液-固界面的铺展与润湿情况,理解气-固表面的吸附本质及 吸附等温线的主要类型,能解释简单的表面反应动力学在不同的压力下 的反应级数。 教学内容提要 时间分配 13.1、表面自由能与表面张力:(表面张力、表面热力学的基本公式、 表面张力与温度的关系、表面张力与溶液浓度的关系) 13.2、弯曲表面上的附加压力和蒸气压 (弯曲液面下的附加压力、杨-拉普拉斯公式、弯曲表面上的蒸气压) 13.3、溶液的表面吸附,表面活性物质 (溶液表面层的吸附现象、吉布斯等温式、表面活性物质的基本性 质及分类) 13.4、几种重要的界面现象及表面活性剂的作用 (润温、乳化、加溶、起泡、去污) 13.5、固体表面的吸附:(兰缪尔吸附等温式、弗纶德利希等温式、 BET 公式、化学与物理吸附) 13.6、气-固相表面催化反应 1 2 1.5 0.5 0.5 0.5 重点 难点 重点:1.表面自由能与表面张力的概念;2.弯曲表面上的附加压力和蒸 气压;3.溶液的表面吸附的吉布斯等温式;4.表面活性剂的原理及其作 用;5.兰缪尔吸附等温式、BET 理论及其公式应用 难点:1.表面自由能与表面张力;2.弯曲表面上的附加压力和毛细现象 3.吉布斯吸附超量;4.表面活性剂;5.固体自溶液中的吸附;6.气-固吸 附作用 讨论 思考 作业 讨论题目:1、为什么液滴和小气泡总是呈球状,而不会呈别的几何形 状?为什么液滴越小,越更接近球形? 2、两块平行玻璃干燥时,叠放 在一起,很容易分开,若在其间放些水叠放在一起却很难分开,为什么? 思考题目:试说明人工降雨、暴沸和防止暴沸、锄地保墒的原理。 练习作业:1、复习题:1、2、3、6、10、16 2、习题: 22 教学手段 课堂讲授 参考 文献 1.王绪。物理化学学习指导。陕西人民教育出版社,1992 2.物理化学——概念辨析解题方法。中国科学技术大学出版社.2002
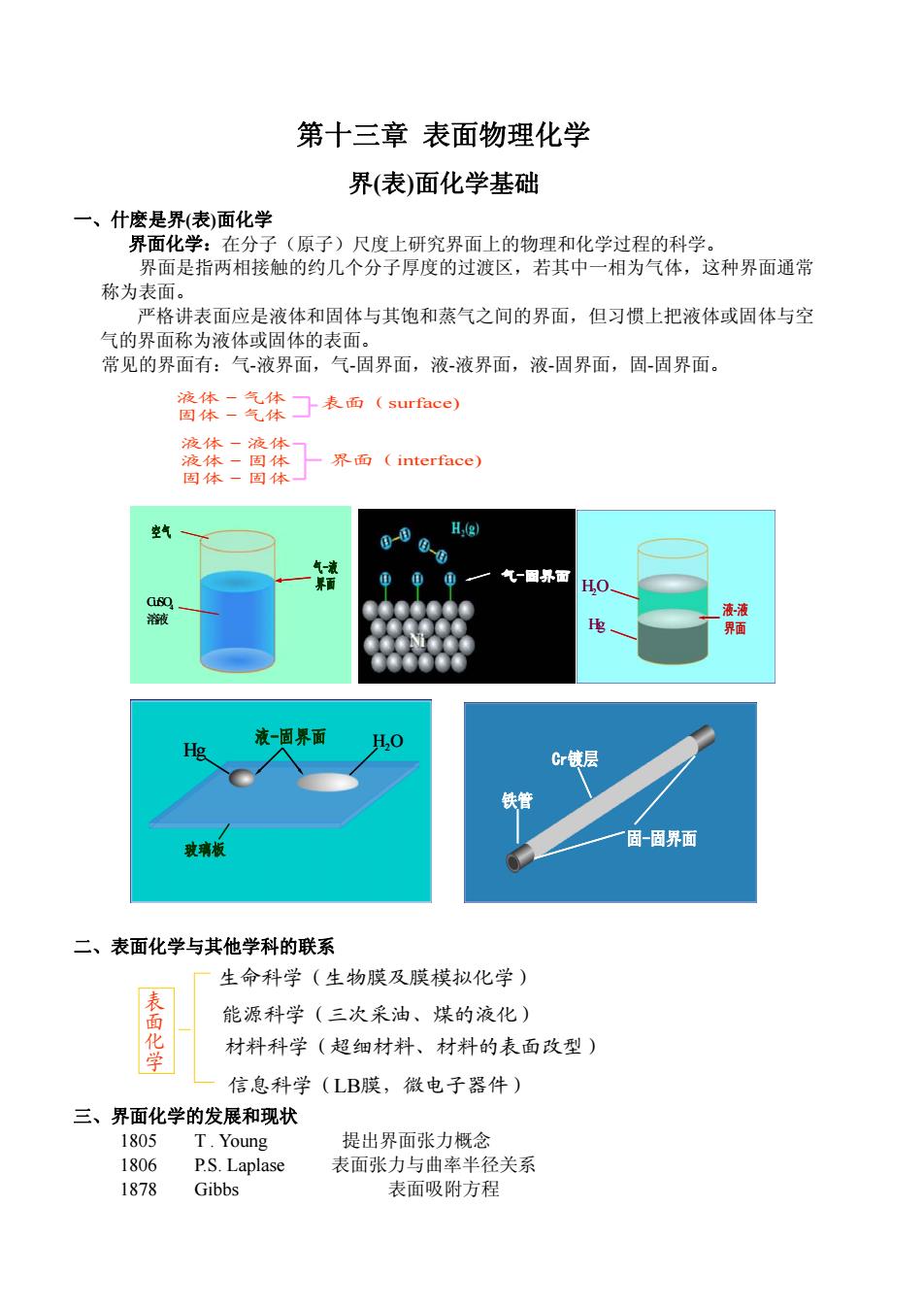
第十三章表面物理化学 界(表)面化学基础 一、什麽是界(表)面化学 界面化学:在分子(原子)尺度上研究界面上的物理和化学过程的科学。 界面是指两相接触的约几个分子厚度的过渡区,若其中一相为气体,这种界面通常 称为表面。 严格讲表面应是液体和固体与其饱和蒸气之间的界面,但习惯上把液体或固体与空 气的界面称为液体或固体的表面。 常见的界面有:气-液界面,气-固界面,液-液界面,液-固界面,固-固界面。 流体二气体丁表面(surface)) 固体一气体 液体一液体 液体一固体 界面(interface) 固体一固体 空气 H.(g) 气一园界面 HO GsO 液液 溶液 电 界面 液-固界面 Hg H,0 Cr铁层 铁管 玻璃板 固固界面 二、表面化学与其他学科的联系 生命科学(生物膜及膜模拟化学) 表面 能源科学(三次采油、煤的液化) 学 材料科学(超细材料、材料的表面改型) 信息科学(LB膜,微电子器件) 三、界面化学的发展和现状 1805 T.Young 提出界面张力概念 1806 P.S.Laplase 表面张力与曲率半径关系 1878 Gibbs 表面吸附方程
第十三章 表面物理化学 界(表)面化学基础 一、什麽是界(表)面化学 界面化学:在分子(原子)尺度上研究界面上的物理和化学过程的科学。 界面是指两相接触的约几个分子厚度的过渡区,若其中一相为气体,这种界面通常 称为表面。 严格讲表面应是液体和固体与其饱和蒸气之间的界面,但习惯上把液体或固体与空 气的界面称为液体或固体的表面。 常见的界面有:气-液界面,气-固界面,液-液界面,液-固界面,固-固界面。 液体-气体 固体-气体 表面(surface) 液体-液体 液体-固体 固体-固体 界面(interface) 空气 CuSO4 溶液 气-液 界面 气-固界面 H O2 Hg 液-液 界面 玻璃板 Hg 液-固界面 H O2 铁管 Cr镀层 固-固界面 二、表面化学与其他学科的联系 表面化学 生命科学(生物膜及膜模拟化学) 能源科学(三次采油、煤的液化) 材料科学(超细材料、材料的表面改型) 信息科学(LB膜,微电子器件) 三、界面化学的发展和现状 1805 T . Young 提出界面张力概念 1806 P.S. Laplase 表面张力与曲率半径关系 1878 Gibbs 表面吸附方程

1916 Langmuir 固体吸附等温方程式 表面与界面化学虽是物理化学的传统研究领域,但由于电子能谱、扫描隧道显微镜 等新的实验技术的出现,使得表面、界面效应及粒子尺寸效应的知识呈指数上升式的积 累,提出了在分子水平上进行基础研究的要求。当前涉及这一领域的研究已成为催化、 电化学、胶体化学的前沿课题,并与生命科学、材料科学、环境科学、膜技术及医药学 密切相关,是这些相关学科要研究和解决的核心课题之一。 四、比表面(specific surface area) 1.定义:比表面用来表示物质分散的程度,有两种常用的表示方法:一种是单位质量的 固体所具有的表面积:另一种是单位体积固体所具有的表面积。即: Am A/m 或 Ay A/V 式中,m和V分别为固体的质量和体积,A为其表面积。目前常用的测定表面积的 方法有BET法和色谱法。 2.分散度与比表面 把物质分散成细小微粒的程度称为分散度。把一定大小的物质分割得越小,则分 散度越高,比表面也越大。 例如,把边长为1cm的立方体1cm3逐渐分割成小立方体时,比表面增长情况列于 下表:P84 边长lm 立方体数 比表面A/ 1×10-2 1 6×102 1×10-3 103 6×103 1×105 109 6×105 1×10-7 1015 6×107 1×109 1021 6×109 从表上可以看出,当将边长为10m的立方体分割成10m的小立方体时,比表面增 长了一千万倍。 可见达到m级的超细微粒具有巨大的比表面积,因而具有许多独特的表面效应, 成为新材料和多相催化方面的研究热点
1916 Langmuir 固体吸附等温方程式 表面与界面化学虽是物理化学的传统研究领域,但由于电子能谱、扫描隧道显微镜 等新的实验技术的出现,使得表面、界面效应及粒子尺寸效应的知识呈指数上升式的积 累,提出了在分子水平上进行基础研究的要求。当前涉及这一领域的研究已成为催化、 电化学、胶体化学的前沿课题,并与生命科学、材料科学、环境科学、膜技术及医药学 密切相关,是这些相关学科要研究和解决的核心课题之一。 四、、比表面(specific surface area) 1.定义:比表面用来表示物质分散的程度,有两种常用的表示方法:一种是单位质量的 固体所具有的表面积;另一种是单位体积固体所具有的表面积。即: / / A Am A AV m V = 或 = 式中,m 和 V 分别为固体的质量和体积,A 为其表面积。目前常用的测定表面积的 方法有 BET 法和色谱法。 2.分散度与比表面 把物质分散成细小微粒的程度称为分散度。把一定大小的物质分割得越小,则分 散度越高,比表面也越大。 例如,把边长为 1 cm的立方体 1 cm3 逐渐分割成小立方体时,比表面增长情况列于 下表:P884 边长l/m 立方体数 比表面Av / (m2 1×10/m-23) 1 6 ×102 1×10-3 103 6 ×103 1×10-5 109 6 ×105 1×10-7 1015 6 ×107 1×10-9 1021 6 ×109 边长l/m 立方体数 比表面Av / (m2 1×10/m-23) 1 6 ×102 1×10-3 103 6 ×103 1×10-5 109 6 ×105 1×10-7 1015 6 ×107 1×10-9 1021 6 ×109 从表上可以看出,当将边长为 10-2m的立方体分割成 10-9m的小立方体时,比表面增 长了一千万倍。 可见达到 nm 级的超细微粒具有巨大的比表面积,因而具有许多独特的表面效应, 成为新材料和多相催化方面的研究热点

第一节表面吉布斯自由能和表面张力 一、界面现象的本质 表面层分子与内部分子相比,它们所处的环境不同。 体相内部分子所受四周邻近相同分子的作用力是对称的,各个方向的力彼此抵销: 但是处在界面层的分子,一方面受到体相内相同物质分子的作用,另一方面受到性 质不同的另一相中物质分子的作用,其作用力未必能相互抵销,因此,界面层会显示出 一些独特的性质。 G 气相 对于单组分体系,这种特性主要来自于同一物质在不同相中的密度不同:对于多组 分体系,则特性来自于界面层的组成与任一相的组成均不相同。 最简单的例子是液体及其蒸气组成的表面。 液体内部分子所受的力可以彼此抵销,但表面分子受到体相分子的拉力大,受到气 相分子的拉力小(因为气相密度低),所以表面分子受到被拉入体相的作用力。这种作 用力使表面有自动收缩到最小的趋势,并使表面层显示出一些独特性质,如表面张力、 表面吸附、毛细现象、过饱和状态等。 二、表面功(surface work) 由于表面层分子的受力情况与本体中不同,因此如果要把分子从内部移到界面,或 可逆的增加表面积,就必须克服体系内部分子之间的作用力,对体系做功。 温度、压力和组成恒定时,可逆使表面积增加dA所需要对体系作的功,称为表(界) 面功。用公式表示为:δW=ydA=dG 式中y为比例系数,它在数值上等于当T,p及组成恒定的条件下,增加单位表面 积时所必须对体系做的可逆非膨胀功。 三、表面自由能(surface free energy))一(比)表面Gibbs函数 考虑了表面功,热力学基本公式中应相应增加ydA一项,即: dG=-SdT+VdptΣμdn。8w' 8W’=-YdA 表面热力学基本关系式 dU TdS -pdW+∑μdng+ydA dH Tds Vdp uadn a+ydA dA =-SdT-pdv undn n ydA dG =-SdT Vdp ugdn g +ydA U 由此可得:y=( )T,P.ng
第一节 表面吉布斯自由能和表面张力 一、界面现象的本质 表面层分子与内部分子相比,它们所处的环境不同。 体相内部分子所受四周邻近相同分子的作用力是对称的,各个方向的力彼此抵销; 但是处在界面层的分子,一方面受到体相内相同物质分子的作用,另一方面受到性 质不同的另一相中物质分子的作用,其作用力未必能相互抵销,因此,界面层会显示出 一些独特的性质。 G L 对于单组分体系,这种特性主要来自于同一物质在不同相中的密度不同;对于多组 分体系,则特性来自于界面层的组成与任一相的组成均不相同。 最简单的例子是液体及其蒸气组成的表面。 液体内部分子所受的力可以彼此抵销,但表面分子受到体相分子的拉力大,受到气 相分子的拉力小(因为气相密度低),所以表面分子受到被拉入体相的作用力。这种作 用力使表面有自动收缩到最小的趋势,并使表面层显示出一些独特性质,如表面张力、 表面吸附、毛细现象、过饱和状态等。 二、表面功(surface work) 由于表面层分子的受力情况与本体中不同,因此如果要把分子从内部移到界面,或 可逆的增加表面积,就必须克服体系内部分子之间的作用力,对体系做功。 温度、压力和组成恒定时,可逆使表面积增加 dA 所需要对体系作的功,称为表(界) 面功。用公式表示为: ' δW A = γ d =dG 式中 γ 为比例系数,它在数值上等于当 T,p 及组成恒定的条件下,增加单位表面 积时所必须对体系做的可逆非膨胀功。 三、表面自由能(surface free energy)—(比)表面 Gibbs 函数 考虑了表面功,热力学基本公式中应相应增加 γdA 一项,即: dG = -SdT+Vdp+ΣμBdnB-δw’ δw’= -γdA 表面热力学基本关系式 VdpSdTdG ++−= ∑ + dAdn BB γμ d SdT pdV dAdn VdpTdSdH dAdn TdSdU pdV dAdn BB BB BB μ γ μ γ μ γ +−−=Α + ++= + +−= + ∑ ∑ ∑ VdpSdTdG ++−= ∑ + dAdn BB γμ d SdT pdV dAdn VdpTdSdH dAdn TdSdU pdV dAdn BB BB BB μ γ μ γ μ γ +−−=Α + ++= + +−= + ∑ ∑ ∑ 由此可得: B ,, )( nVS A U ∂ ∂ = B ,, )( nPS A H ∂ ∂ = B ,, )( nVT A F ∂ ∂ = B ,, )( nPT A G ∂ ∂ γ =