
1.1.4物理模型 对真实的物理过程和对象,根据所讨论的问题的基本要 求对其进行理想化的简化,抽象为可以用数学方法描述的理 想模型。 *关于物理模型的提出 (1)明确所提问题; (2)分析各种因素在所提问题中的主次; (3)突出主要因素,提出理想模型; (4)实验验证。 “理想模型”是对所考察的问题来说的,不具有绝对意义。 首页上页下页退出
首 页 上 页 下 页 退 出 6 1.1.4 物理模型 对真实的物理过程和对象,根据所讨论的问题的基本要 求对其进行理想化的简化,抽象为可以用数学方法描述的理 想模型。 *关于物理模型的提出 (1)明确所提问题; (3)突出主要因素,提出理想模型; “理想模型”是对所考察的问题来说的,不具有绝对意义。 (2)分析各种因素在所提问题中的主次; (4)实验验证

1、理想质点模型 一选用质点模型的前提条件是: 物体自身线度与所研究的物体运动的空间范围相比可以忽略; 或者物体只作平动。 两个条件中,具一即可。 一真实的物体不满足上述条件时,则可将其视为满足第一个 条件的质点系。 首页上页下页退出
首 页 上 页 下 页 退 出 7 1、 理想质点模型 真实的物体不满足上述条件时,则可将其视为满足第一个 条件的质点系。 选用质点模型的前提条件是: 物体自身线度l与所研究的物体运动的空间范围r相比可以忽略; 两个条件中,具一即可。 或者物体只作平动

2、理想刚体模型 当物体自身线度与所研究的物体运动的空间范围比不可 以忽略;物体又不作平动时,即必须考虑物体的空间方位, 我们可以引入刚体模型。 刚体是指在任何情况下,都没有形变的物体。 刚体也是一个各质点之间无相对位置变化且质量连续分布 的质点系。 首页上页下页退出
首 页 上 页 下 页 退 出 8 2、理想刚体模型 刚体是指在任何情况下,都没有形变的物体。 当物体自身线度l与所研究的物体运动的空间范围r比不可 以忽略;物体又不作平动时,即必须考虑物体的空间方位, 我们可以引入刚体模型。 刚体也是一个各质点之间无相对位置变化且质量连续分布 的质点系
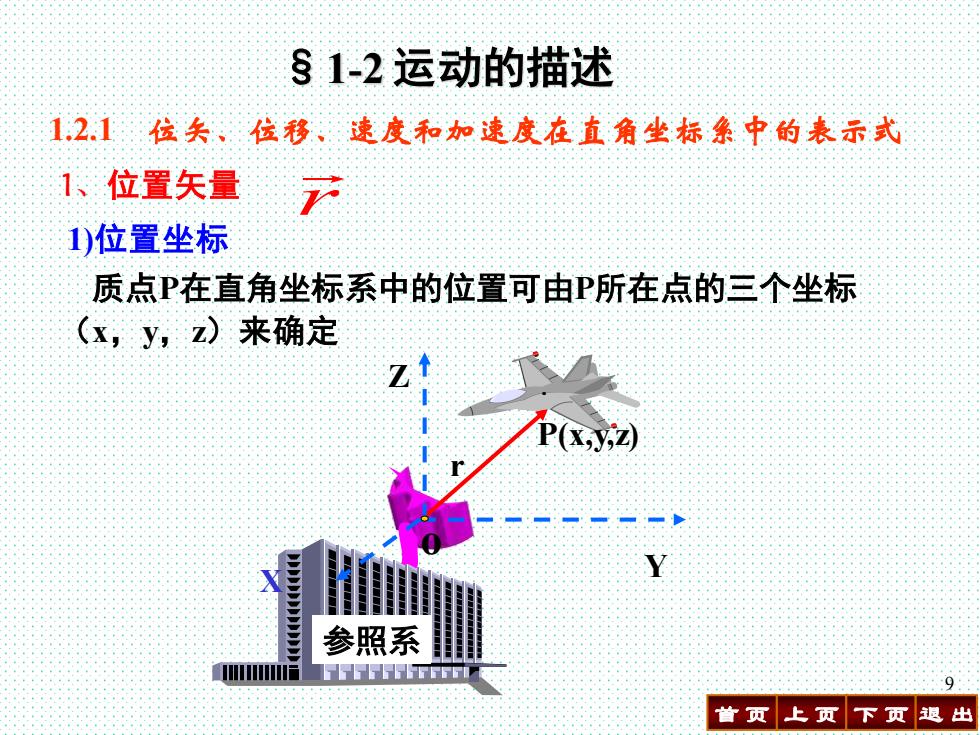
§1-2运动的描述 1.2.1位关、位移、速度和加速度在直角坐标系中的表示式 1、位置矢量 1)位置坐标 质点P在直角坐标系中的位置可由P所在点的三个坐标 (x,y,z)来确定 P(xy,z) 参照系 11516166五Fi 首页上页下页退出
首 页 上 页 下 页 退 出 9 1)位置坐标 §1-2 运动的描述 1、位置矢量 r 质点P在直角坐标系中的位置可由P所在点的三个坐标 (x,y,z)来确定 1.2.1 位矢、位移、速度和加速度在直角坐标系中的表示式 参照系 r Y Z X o P(x,y,z)

2)位置矢量r 由坐标原点引向考察点的矢 量,简称位矢。 其在直角坐标系中为 F=xi+以i+zk =√x2+y2+z2 的方向余弦是 cosa-x c0sB-xc0s7- r cos a+cos B+cosy=1 在极坐标系中 F=rTo 在自然坐标系中 下=F(S) 首页上页下页退出
首 页 上 页 下 页 退 出 10 2)位置矢量r z k r 0 j y i x 其在直角坐标系中为 r xi yj zk = + + 2 2 2 r = x + y + z 由坐标原点引向考察点的矢 量,简称位矢。 r的方向余弦是 r x cos α = r y cos β = r z cosγ = 1 2 2 2 cos + cos + cos = 在极坐标系中 0 r rr = 在自然坐标系中 r r(s) =