
通信原理 第3章随机过程
1 通信原理 第3章 随机过程

第3章随机过程 ● 3.1随机过程的基本概念 ■什么是随机过程? ◆随机过程是一类随时间作随机变化的过程,它不能 用确切的时间函数描述。可从两种不同角度看: ◆角度1:对应不同随机试验结果的时间过程的集合。 2
2 第3章 随机过程 ⚫ 3.1 随机过程的基本概念 ◼ 什么是随机过程? ◆ 随机过程是一类随时间作随机变化的过程,它不能 用确切的时间函数描述。可从两种不同角度看: ◆ 角度1:对应不同随机试验结果的时间过程的集合
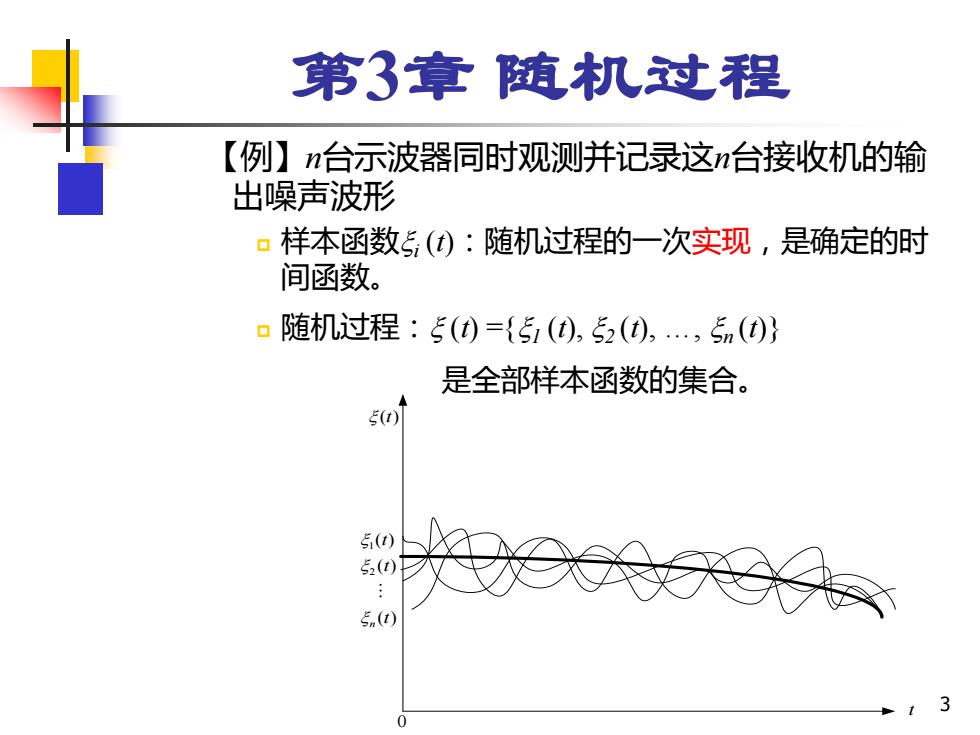
第3章随机过程 【例】n台示波器同时观测并记录这n台接收机的输 出噪声波形 ▣样本函数5():随机过程的一次实现,是确定的时 间函数。 口随机过程:5(t)={51(),52(t),.,5n()} 是全部样本函数的集合。 5u) 5() 52(t)) 5n(0
3 第3章 随机过程 【例】n台示波器同时观测并记录这n台接收机的输 出噪声波形 样本函数i (t):随机过程的一次实现,是确定的时 间函数。 随机过程: (t) ={1 (t), 2 (t), ., n (t)} 是全部样本函数的集合。 ()t t 0 1 2 ( ) ( ) ( ) n t t t

第3章随机过程 角度2:随机过程是随机变量概念的延伸 ▣在任一给定时刻1上,每一个样本函数5(都是一个确定的 数值,(t),但是每个5(t)都是不可预知的。 ▣在一个固定时刻t上,不同样本的取值{(t),i=1,2,.,n} 是一个随机变量,记为5(t)。 口换句话说,随机过程在任意时刻的值是一个随机变量。 ▣因此,我们又可以把随机过程看作是在时间进程中处于不同 时刻的随机变量的集合。 ▣这个角度更适合对随机过程理论进行精确的数学描述。 A
4 第3章 随机过程 ◆ 角度2:随机过程是随机变量概念的延伸。 在任一给定时刻t1上,每一个样本函数i (t)都是一个确定的 数值i (t1 ),但是每个i (t1 )都是不可预知的。 在一个固定时刻t1上,不同样本的取值{i (t1 ), i = 1, 2, ., n} 是一个随机变量,记为 (t1 )。 换句话说,随机过程在任意时刻的值是一个随机变量。 因此,我们又可以把随机过程看作是在时间进程中处于不同 时刻的随机变量的集合。 这个角度更适合对随机过程理论进行精确的数学描述

第3章随机过程 ● 3.1.1随机过程的分布函数 ◆设ξ(t)表示一个随机过程,则它在任意时刻t的值(t) 是一个随机变量,其统计特性可以用分布函数或概率密 度函数来描述。 ◆随机过程ξ()的一维分布函数: F(x1,t1)=P[5(t1)≤x] ◆随机过程5()的一维概率密度函数: (x,41)= F (x,4) Ox1 若上式中的偏导存在的话。 5
5 第3章 随机过程 ◼ 3.1.1随机过程的分布函数 ◆ 设 (t)表示一个随机过程,则它在任意时刻t1的值 (t1 ) 是一个随机变量,其统计特性可以用分布函数或概率密 度函数来描述。 ◆ 随机过程 (t)的一维分布函数: ◆ 随机过程 (t)的一维概率密度函数: 若上式中的偏导存在的话。 ( , ) [ ( ) ] 1 1 1 1 1 F x t = P t x 1 1 1 1 1 1 1 ( , ) ( , ) x F x t f x t =