
能量信号与功率信号 电信号可以用瞬时功率p()表示, p(t)=v2(t)/R p()=i2(t)R ■其中v()和()分别是流过电阻的电压和电流。 ·归一化后可统一表示成p()=x2() 在时间间隔(-T,T2》内的能量为E=小r(h 平均功率为:P= T 当且仅当信号在所有时间上的能量不为零且有限(0<E<∞)时,该 信号为能量信号;其中 E,=m2rut=小x(eh 当且仅当信号的平均功率不为零且有限(0<P<∞)时,该信号为功 率信号;其中 B=把7arua
能量信号与功率信号 电信号可以用瞬时功率p(t)表示, p(t)=v2 (t)/R p(t)=i2 (t)R 其中v(t)和i(t)分别是流过电阻的电压和电流。 归一化后可统一表示成p(t)=x2 (t) 在时间间隔(-T/2,T/2)内的能量为 平均功率为: 当且仅当信号在所有时间上的能量不为零且有限(0<Ex <∞)时,该 信号为能量信号;其中 当且仅当信号的平均功率不为零且有限(0<Px <∞)时,该信号为功 率信号;其中 / 2 2 / 2 ( ) T T x T E x t dt T T x x E P T / 2 2 2 / 2 lim ( ) ( ) T x T T E x t dt x t dt / 2 2 / 2 1 lim ( ) T x T T P x t dt T

很显然,能量信号的能量有限而平均功率为0,功率信号的 平均功率有限而能量无穷大。 。我们一般将模拟信号归为功率信号,因为模拟波形的持续时 间为无限长,能量是无穷大的,不能用能量来描述该信号, 功率(能量传输速率)更有意义; 冬数字系统中,一般都是用码元间隔为Ts的波形来发送和接收 码元,每个码元的平均功率(在整个时间轴上取平均)为0, 所以功率不能用于描述数字信号。因此,对于数字信号应该 采用能在时间窗内度量信号的测度,即码元能量(功率在Ts 上的积分)更有意义。 一般来说,周期信号和随机信号是功率信号,非周期的确定 信号是能量信号
很显然,能量信号的能量有限而平均功率为0,功率信号的 平均功率有限而能量无穷大。 我们一般将模拟信号归为功率信号,因为模拟波形的持续时 间为无限长,能量是无穷大的,不能用能量来描述该信号, 功率(能量传输速率)更有意义; 数字系统中,一般都是用码元间隔为Ts的波形来发送和接收 码元,每个码元的平均功率(在整个时间轴上取平均)为0, 所以功率不能用于描述数字信号。因此,对于数字信号应该 采用能在时间窗内度量信号的测度,即码元能量(功率在Ts 上的积分)更有意义。 一般来说,周期信号和随机信号是功率信号,非周期的确定 信号是能量信号

频谱密度 频谱密度:信号的能量或功率在频域上的分布特性。 能量谱密度(ESD) 利用Parsevals定理,信号x()在时域和频域的能量表达式为: E.=∫x2(dt=X(f)f 其中X0是x(0的傅立叶变换,设平.f)=X(f乃则平(f)就是x的能 量谱密度。 冬功率谱密度(PSD) ■设x()是周期为T的周期信号(功率信号),则在信号周期T。上的平均功 率为: 1=-o0 其中c是周期信号傅立叶级数的复系数的幅值。 功率谱密度 G,(f)=∑c2δf-nf%)
频谱密度 频谱密度:信号的能量或功率在频域上的分布特性。 能量谱密度(ESD) 利用Parseval定理,信号x(t)在时域和频域的能量表达式为: 其中X(f)是x(t)的傅立叶变换,设 ,则 就是x(t)的能 量谱密度。 功率谱密度(PSD) 设x(t)是周期为T0的周期信号(功率信号),则在信号周期T0上的平均功 率为: 其中|cn |是周期信号傅立叶级数的复系数的幅值。 功率谱密度 2 2 ( ) ( ) E x t dt X f df x 2 ( ) ( ) x f X f ( ) x f 0 0 / 2 2 2 / 2 0 1 ( ) T x n T n P x t dt c T 2 0 ( ) ( ) x n n G f c f nf

G()的几个性质 1.G(①20,且为实数; 2.Gx(①=Gx(-f),对实值x): 3.Gx(⑤←→R(T),PSD与自相关函数是傅立叶变换对; 4.P=G,(f)f,归一化平均功率与PSD之间的关系。 研究平,(f)和G,(f)的目的,主要为研究信号能量或功 率在频域内的分布规律,以便合理地选择信号的通频带, 对传输电路提出恰当的频带要求,尽量做到在信号不失 真或失真不大的条件下提高信噪比
研究 和 的目的,主要为研究信号能量或功 率在频域内的分布规律,以便合理地选择信号的通频带, 对传输电路提出恰当的频带要求,尽量做到在信号不失 真或失真不大的条件下提高信噪比。 ( ) x f ( ) G f x 1. Gx (f) ≥0,且为实数; 2. Gx (f)=Gx (-f),对实值x(t); 3. Gx (f) Rx ( ) ,PSD与自相关函数是傅立叶变换对; ( ) P G f df x x 4. ,归一化平均功率与PSD之间的关系。 Gx (f)的几个性质
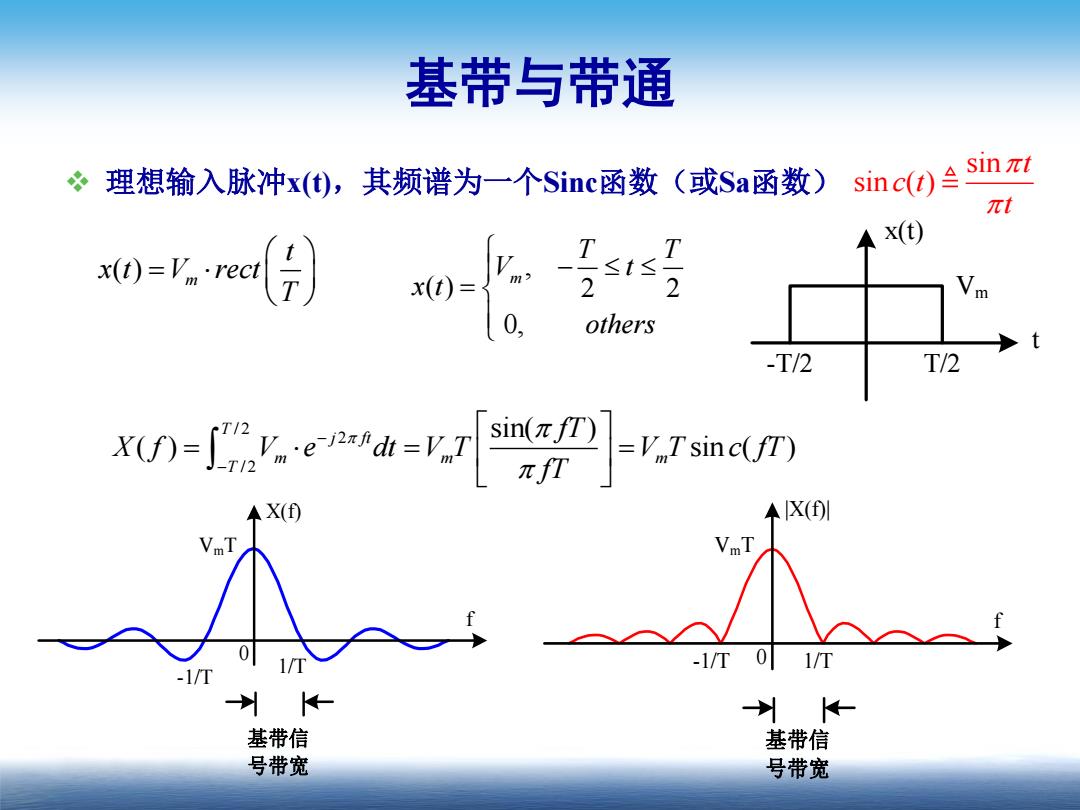
基带与带通 理想输入脉冲x(),其频谱为一个Sinc函数(或Sa函数)sinc(t)会 lnπt πt x(t) x(t)=Vrect 2 Vm 0, others -T/2 T/2 F.T sncUt) ◆X(f ◆X() VmT VmT 0 -1/T01/T 州← 基带信 基带信 号带宽 号带宽
基带与带通 理想输入脉冲x(t),其频谱为一个Sinc函数(或Sa函数) , ( ) 2 2 0, m T T V t x t others ( ) m t x t V rect T sin sin ( ) t c t t / 2 2 / 2 sin( ) ( ) sin ( ) T j ft m m m T fT X f V e dt V T V T c fT fT x(t) t -T/2 T/2 Vm VmT f X(f) 0 -1/T 1/T 基带信 号带宽 VmT f |X(f)| -1/T 0 1/T 基带信 号带宽