山东第一医科大学（泰山医学院）：《数据结构》课程教学资源（PPT课件）第5章 数组和广义表

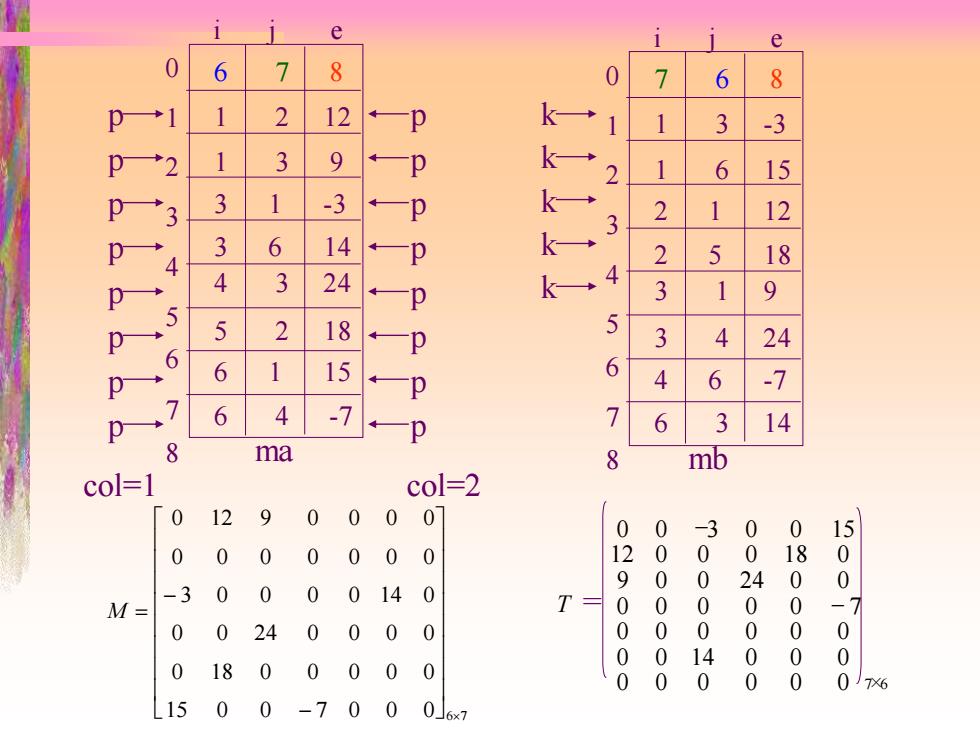
e 6 8 7 8 2 12 p 3 3 3 9 6 15 3 1 -3 p 3 2 12 3 6 14 k一 2 5 18 4 3 24 k→ 3 1 9 5 P 5 2 18 一p 3 4 24 6 1 15 6 4 6 -7 p.7 6 4 -7 p 7 6 3 14 8 ma P mb col=1 col=2 12 9 0 00 0 0 0 -3 0 0 15 0 0 0 0 0 00 0 0 0 18 9 0 0 -3 0 0 0140 24 0 0 M= 0 T 0 0 0 24 0 00 0 0 0 0 00 00 0 0 0 14 0 0 0 18 0 0 00 0 0 0 0 0 0J76 15 0 0 -70 0 0J6x7

6 7 8 1 2 12 1 3 9 3 1 -3 3 6 14 4 3 24 5 2 18 6 1 15 6 4 -7 i j e 012345678 ma 7 6 8 1 3 -3 1 6 15 2 1 12 2 5 18 3 1 9 3 4 24 4 6 -7 6 3 14 i j e 012345678 mb p k ppppppp kkkk pppppppp col=1 col=2 15 0 0 7 0 0 0 6 7 0 18 0 0 0 0 0 0 0 24 0 0 0 0 3 0 0 0 0 14 0 0 0 0 0 0 0 0 0 12 9 0 0 0 0    − − M = − 7 0 0 0 0 0 0 0 0 14 0 0 0 0 0 0 0 0 0 0 0 0 0 0 9 0 0 24 0 0 12 0 0 0 18 0 0 0 3 0 0 15 7 ×6 T ＝ −

Status TransposeSMatrix(TSMatrix M,TSMatrix &T){ /采用三元组表存储表示，求稀疏矩阵M的转置矩阵T。 T.mu=M.nu;T.nu=M.mu;T.tu-M.tu; if (T.tu){ q=1; for(col=1;col<=M.nu;++col) for (p=1;p<=M.tu;++p) if (M.data[p]j=col){ T.data[q].i=M.data[p]j;T.data[q].j=M.data[p].i; T.data[q].e=M.data[p].e;++q; return OK; //TransposeSMatrix eturn

Status TransposeSMatrix(TSMatrix M, TSMatrix &T) { //采用三元组表存储表示，求稀疏矩阵M的转置矩阵T。 T.mu=M.nu; T.nu=M.mu; T.tu=M.tu; if (T.tu) { q=1; } return OK; }//TransposeSMatrix return for (col=1; col<=M.nu; ++col) for (p=1; p<=M.tu; ++p) if (M.data[p].j==col) { T.data[q].i=M.data[p].j; T.data[q].j=M.data[p].i; T.data[q].e=M.data[p].e; ++q;}

方法二：稀疏矩阵的快速转置 算法思想是：以M矩阵的三元组为中心，依次取出M.data中的每一 个三元组，交换行列后 直接将其写入T.data合适的位置中。 0 1290000 e e 0 030015 0 000000 12000180 0 6 8 8 -300 00140 90 0240 0 1 2 12 M= T00 0 0 -7 0 02400 00 0 00 0 0 0 0 2 3 9 2 15 0180 000 00 1 00 0 3 3 1 -3 3 2 12 15 00-700067 000 0 0 0% 3 6 14 4 2 5 18 4 24 5 3 9 如果能先求得M各列 5 2 18 6 3 4 24 第一个非零元三元组在T.data中的位置 6 1 15 7 4 6 -7 就能在对M.data一次扫描的过程中， 完成M到T的转置 8 6 4 -7 8 6 3 14 M.data T.data

方法二：稀疏矩阵的快速转置 算法思想是：以M矩阵的三元组为中心, 依次取出 M.data 中的每一 个三元组，交换行列后，直接将其写入T.data合适的位置中。 6 7 8 1 2 12 1 3 9 3 1 -3 3 6 14 4 3 24 5 2 18 6 1 15 6 4 -7 i j e 0 1 2 3 4 5 6 7 8 M.data i j e 0 1 2 3 4 5 6 7 8 T.data 7 6 8 2 1 12 1 3 -3 1 6 15 2 5 18 3 1 9 3 4 24 4 6 -7 6 3 14 15 0 0 7 0 0 0 6 7 0 18 0 0 0 0 0 0 0 24 0 0 0 0 3 0 0 0 0 14 0 0 0 0 0 0 0 0 0 12 9 0 0 0 0                      − − M = − 7 0 0 0 0 0 0 1 0 0 0 4 0 0 0 0 0 0 0 0 0 0 0 0 0 9 0 0 24 0 0 12 0 0 0 18 0 0 0 3 0 0 15 7×6 T ＝ − 如果能先求得M各列 第一个非零元三元组在T.data 中的位置 就能在对M.data一次扫描的过程中， 完成M到T的转置

实现：引入两辅助数组 num[col]: 存储矩阵M中第col列中非零元个数 cpot[col:存储M中第col列第一个非零元在T.data中位置 显然有： cpot[1]=1; cpot[col]-=cpot[col-1]+num[col-1]; (2≤col≤M.nu 0 129000 0 0 0 0 0 00 0 col 2 6 7 -30 0 0014 0 M= 0 024 000 0 num[col] 2 0 0 18 0 0 0 0 0 cpot[col] 8 8 1500-7 00 06x1

实现：引入两辅助数组 num[col]：存储矩阵M中第col列中非零元个数 cpot[col]：存储M中第col列第一个非零元在T.data中位置 显然有： cpot[1]=1; cpot[col]=cpot[col-1]+num[col-1]; (2≤col ≤M.nu) 1 3 5 7 8 8 9 col num[col] cpot[col] 1 2 2 2 3 2 4 1 5 0 6 1 7 0 15 0 0 7 0 0 0 6 7 0 18 0 0 0 0 0 0 0 24 0 0 0 0 3 0 0 0 0 14 0 0 0 0 0 0 0 0 0 12 9 0 0 0 0                      − − M =