山东第一医科大学（泰山医学院）：《数据结构》课程教学资源（PPT课件）第5章 数组和广义表

稀疏矩阵的压缩存储方法 三元组顺序表 行逻辑连接的倾序表 十字链表

❖稀疏矩阵的压缩存储方法 三元组顺序表 行逻辑链接的顺序表 十字链表

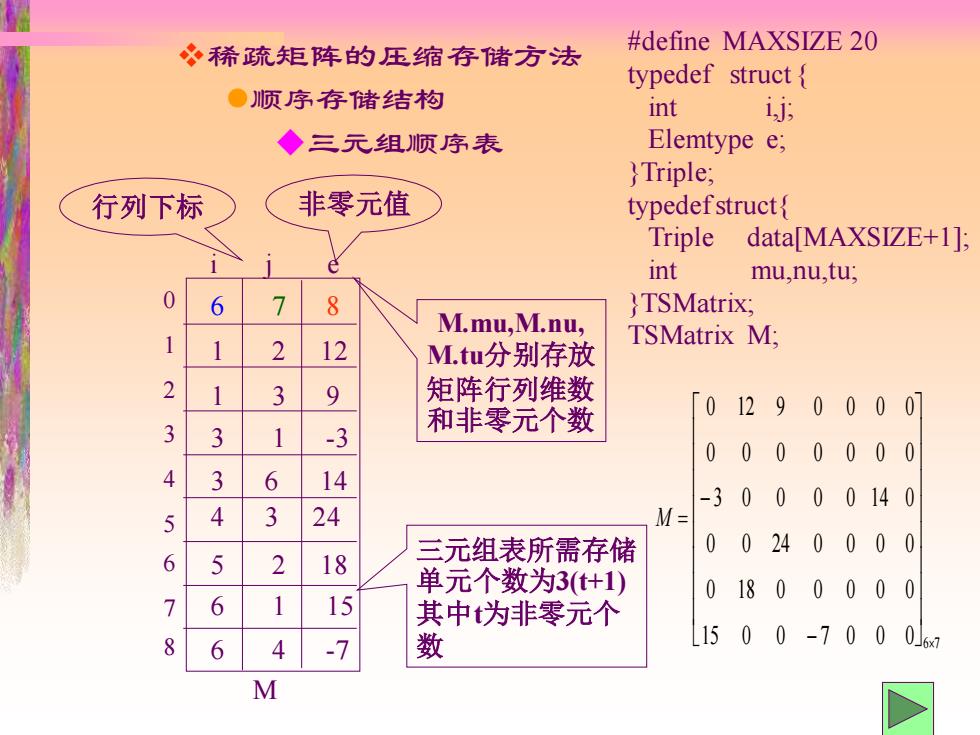
稀疏矩阵的压缩存储方法 #define MAXSIZE 20 typedef struct{ ●顺序存储结构 int ij; ◆三元组顺序表 Elemtype e; }Triple; 行列下标 非零元值 typedefstruct Triple data[MAXSIZE+1]; int mu,nu,tu; 0 6 8 }TSMatrix; M.mu,M.nu, 2 12 TSMatrix M; M.tu分别存放 2 3 矩阵行列维数 和非零元个数 0 129 0000 3 3 -3 0000000 4 3 6 14 -30000140 5 4 3 24 M= 三元组表所需存储 00240000 6 5 2 18 单元个数为3(t+1) 15 01800000 7 6 其中为非零元个 1500-700 8 6 4 -7 数 06 M

❖稀疏矩阵的压缩存储方法 ⚫顺序存储结构 ◆三元组顺序表 #define MAXSIZE 20 typedef struct { int i,j; Elemtype e; }Triple; typedef struct{ Triple data[MAXSIZE+1]; int mu,nu,tu; }TSMatrix; TSMatrix M; 三元组表所需存储 单元个数为3(t+1) 其中t为非零元个 数 6 7 8 1 2 12 1 3 9 3 1 -3 3 6 14 4 3 24 5 2 18 6 1 15 6 4 -7 M i j e 0 1 2 3 4 5 6 7 8 M.mu,M.nu, M.tu分别存放 矩阵行列维数 和非零元个数 行列下标 非零元值 15 0 0 7 0 0 0 6 7 0 18 0 0 0 0 0 0 0 24 0 0 0 0 3 0 0 0 0 14 0 0 0 0 0 0 0 0 0 12 9 0 0 0 0                      − − M =

>求转置矩阵 女问题描述：已知一个稀疏矩阵的三元组表， 求该矩阵转置矩阵的三元组表 问题分析 常规的二维数组表示时转置的算法： for(col=1;col<=nu;++col) for(row=1;row<-mu;++row) T[col][row]=M[row][col]: T(n)-O(muxnu)

问题描述：已知一个稀疏矩阵的三元组表， 求该矩阵转置矩阵的三元组表 问题分析 常规的二维数组表示时转置的算法： for(col=1;col<=nu;++col) for(row=1;row<=mu;++row) T[col][row]=M[row][col]; T(n)=O(munu) ➢求转置矩阵

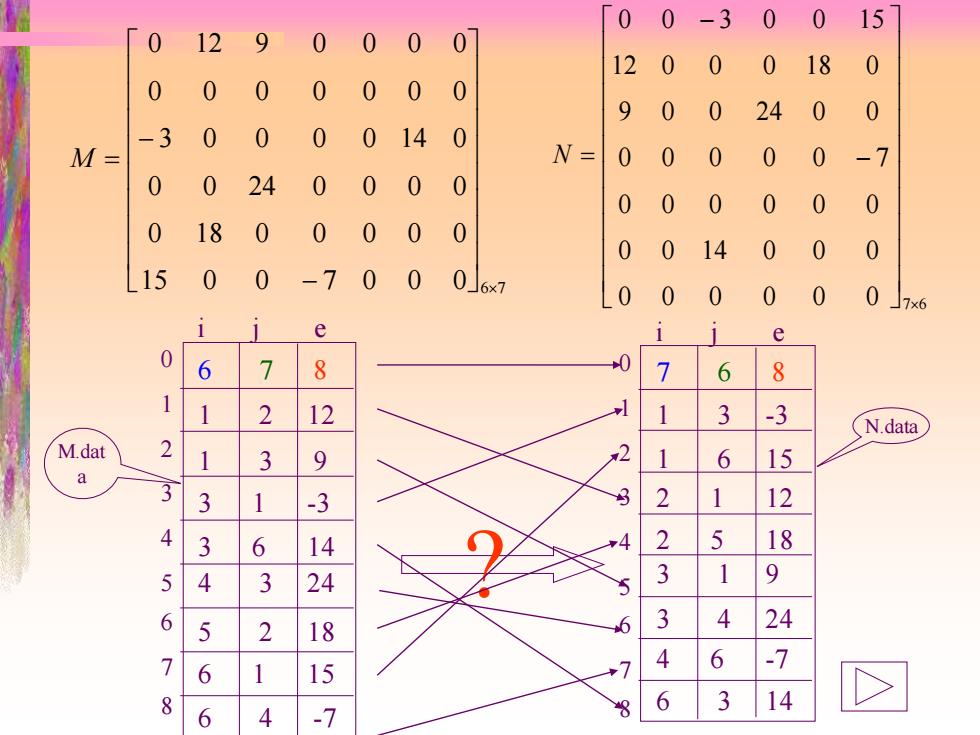
0 0-3 0 0 15 0 12 0 0 0 120 0 0 18 0 0 0 0 0 0 0 0 9 0 0 24 0 0 -3 0 0 0 014 0 M= N= 0 0 0 0 0 -7 0 0 24 0 0 0 0 0 0 0 0 0 0 0 18 0 0 0 0 0 0 0 14 0 0 0 15 0 0 -7 0 0 0」6x7 0 0 0 0 0 0 ☐7×6 1 e 0 6 7 8 7 6 8 1 1 2 12 1 3 -3 N.data M.dat 2 1 3 9 2 1 6 15 a 3 -3 3 2 12 4 3 6 14 2 5 18 5 4 3 24 3 1 9 6 5 4 2 18 24 7 4 6 15 -7 6 8 6 3 14 6 4 -7

15 0 0 7 0 0 0 6 7 0 18 0 0 0 0 0 0 0 24 0 0 0 0 3 0 0 0 0 14 0 0 0 0 0 0 0 0 0 12 9 0 0 0 0    − − M = 0 0 0 0 0 0 7 6 0 0 14 0 0 0 0 0 0 0 0 0 0 0 0 0 0 7 9 0 0 24 0 0 12 0 0 0 18 0 0 0 3 0 0 15    − − N = 6 7 8 1 2 12 1 3 9 3 1 -3 3 6 14 4 3 24 5 2 18 6 1 15 6 4 -7 i j e 012345678 M.dat a i j e 7 6 8 1 3 -3 1 6 15 2 1 12 2 5 18 3 1 9 3 4 24 4 6 -7 6 3 14 012345678 N.data ?

0 129 000 0 0 3 0 15 稀疏矩阵三元组转置算法 0 00 0000 0 0 0 18 -30 0 0014 0 9 0 0 24 0 00 M 0 024 000 T三 0 0 0 0 0 解决思路：只要做到 0 0 0 0 0 180 000 0 0 0 14 0 00 ①将矩阵行、列维数互换 15 00-700 0 0 0 0 0 0 ②将每个三元组中的i和j相互调换 ③重排三元组次序，使T.data中元素以T的行(M的列)为主序 方法一：按M的列序转置 即按T.data中三元组次序依次在M.data中找到相应的三元组 进行转置。为找到M中每一列所有非零元素，需对其三元组表 M.data从第一行起扫描一遍。由于M.data中以M行序为主序， 所以由此得到的恰是T.data中应有的顺序 卒算法分析：T()=O(M的列数n×非零元个数t) 若t与mxn同数量级，则T(nm)=O(m×n2)

解决思路：只要做到 将矩阵行、列维数互换 将每个三元组中的i和j相互调换 重排三元组次序，使T.data中元素以T的行(M的列)为主序 方法一：按M的列序转置 即按T.data中三元组次序依次在M.data中找到相应的三元组 进行转置。为找到M中每一列所有非零元素，需对其三元组表 M.data从第一行起扫描一遍。由于M.data中以M行序为主序, 所以由此得到的恰是T.data中应有的顺序 算法分析：T(n)=O(M的列数n非零元个数t) 若 t 与mn同数量级，则 ( ) ( ) 2 T n = O m n 稀疏矩阵三元组转置算法 15 0 0 7 0 0 0 6 7 0 18 0 0 0 0 0 0 0 24 0 0 0 0 3 0 0 0 0 14 0 0 0 0 0 0 0 0 0 12 9 0 0 0 0                      − − M = − 7 0 0 0 0 0 0 0 0 14 0 0 0 0 0 0 0 0 0 0 0 0 0 0 9 0 0 24 0 0 12 0 0 0 18 0 0 0 3 0 0 15 7×6 T ＝ −