
第六章树 树是一类重要的非线性数据结构,是以分支关 系定义的层次结构 §6.1树的定义和基本术语 ★定义 定义:树(tree)是n(n>0)个结点的有限集T,其中: ●有且仅有一个特定的结点,称为树的根(roo) ●当n>1时,其余结点可分为m(m>0)个互不相交 的有限集T1,T2,..Tm,其中每一个集合本身 又是一棵树,称为根的子树(subtree) 必特点: ●树中至少有一个结点一根 ●树中各子树是互不相交的集合
第六章 树 树是一类重要的非线性数据结构,是以分支关 系定义的层次结构 §6.1 树的定义和基本术语 定义 ❖定义:树(tree)是n(n>0)个结点的有限集T,其中: ⚫有且仅有一个特定的结点,称为树的根(root) ⚫当n>1时,其余结点可分为m(m>0)个互不相交 的有限集T1,T2,……Tm,其中每一个集合本身 又是一棵树,称为根的子树(subtree) ❖特点: ⚫树中至少有一个结点——根 ⚫树中各子树是互不相交的集合
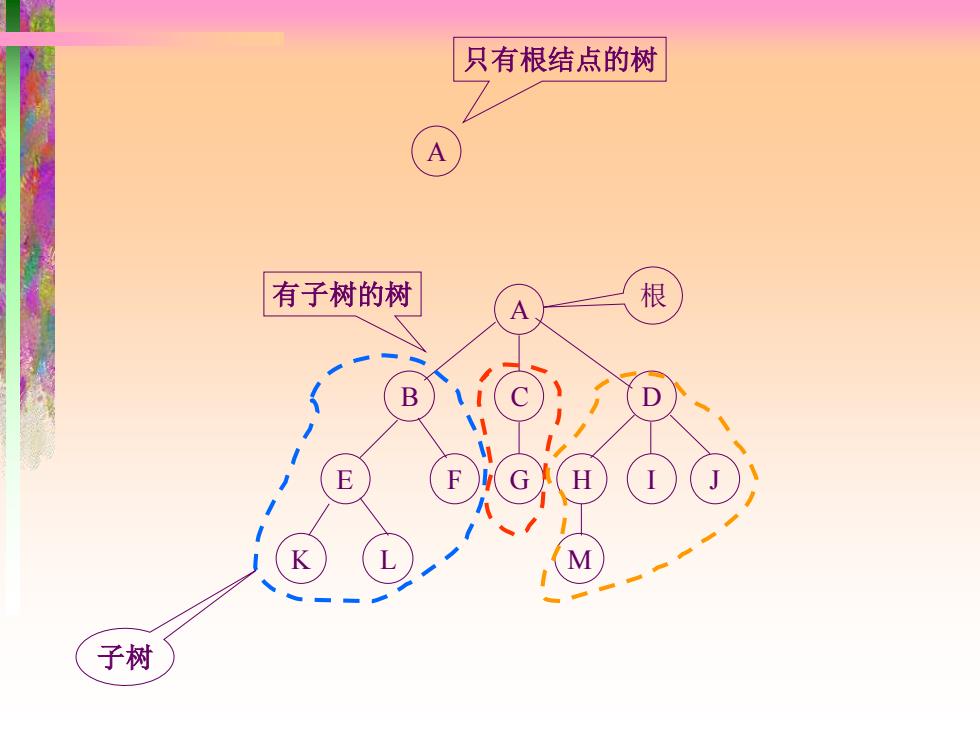
只有根结点的树 有子树的树 根 子树
A 只有根结点的树 A B C D E F G H I J K L M 有子树的树 根 子树

数据对象D: D是具有相同特性的数据元素的集合。 数据关系R: 若D为空集,则称为空树。 否则: (1)在D中存在唯一的称为根的数据元素root; (2)当n>1时,其余结点可分为m(m>0)个互 不相交的有限集T1,T2,,Tm,其中每一 棵子集本身又是一棵符合本定义的树, 称为根root的子树
数据对象 D: D是具有相同特性的数据元素的集合。 若D为空集,则称为空树 。 否则: (1) 在D中存在唯一的称为根的数据元素root; (2) 当n>1时,其余结点可分为m (m>0)个互 不相交的有限集T1 , T2 , …, Tm,其中每一 棵子集本身又是一棵符合本定义的树, 称为根root的子树。 数据关系 R:

基本操作: +查找类 +插入类 +删除类
基本操作: 查 找 类 插 入 类 删 除 类

查找类: Root(T)∥求树的根结点 Value(T,cure)∥求当前结点的元素值 Parent(T,cure)∥求当前结点的双亲结点 LeftChild(T,cure)∥求当前结点的最左孩子 RightSibling(T,cure)∥求当前结点的右兄弟 TreeEmpty(T)∥判定树是否为空树 TreeDepth(T)∥求树的深度 TraverseTree(T,Visit0)∥遍历
Root(T) // 求树的根结点 查找类: Value(T, cur_e) // 求当前结点的元素值 Parent(T, cur_e) // 求当前结点的双亲结点 LeftChild(T, cur_e) // 求当前结点的最左孩子 RightSibling(T, cur_e) // 求当前结点的右兄弟 TreeEmpty(T) // 判定树是否为空树 TreeDepth(T) // 求树的深度 TraverseTree( T, Visit() ) // 遍历