
11.2.1.2评价指标的选择方法 2、定量方法 常用的定量方法有:试算法、聚类分析法和主成分分析法 等几种。 第一种方法:试算法是通过历史资料的试算来判断指标的 有效性。 例如,要评价全国各地区2005年可持续发展战略的实施绩 效,可以2003年和2004年的数据进行试算,通过试算结果判 断所选指标的合适性,然后对相关指标进行科学比较,把那些 代表性强的指标纳入指标体系的构建之中,然后反复修正指标 体系直至满意为止
2、定量方法 常用的定量方法有:试算法、聚类分析法和主成分分析法 等几种。 第一种方法:试算法是通过历史资料的试算来判断指标的 有效性。 例如,要评价全国各地区2005年可持续发展战略的实施绩 效,可以2003年和2004年的数据进行试算,通过试算结果判 断所选指标的合适性,然后对相关指标进行科学比较,把那些 代表性强的指标纳入指标体系的构建之中,然后反复修正指标 体系直至满意为止。 11.2.1.2 评价指标的选择方法

11.2.1.2评价指标的选择方法 2、定量方法 第二种方法:聚类分析法 聚类分析在选择指标方面的基本思路是:如果有若干个指 标,首先将每一个指标看成一类,然后根据指标间的相似程 度,通过比较类间距离进行并类。每次将距离最近的两类加以 合并,余下N-1类。再选择这N-1类中距离最近的两类加以合 并,余下N-2类。依次类推。这样,每合并一次,就减少一 类,继续这一过程,直至将所有指标合并成为一类为止,形成 由小到大的分类系统,即谱系。最后整个分类结果画在一张图 上,称为聚类图或谱系图,以此直观地反映各指标间的亲疏关 系
2、定量方法 第二种方法:聚类分析法 聚类分析在选择指标方面的基本思路是:如果有若干个指 标,首先将每一个指标看成一类,然后根据指标间的相似程 度,通过比较类间距离进行并类。每次将距离最近的两类加以 合并,余下N-1类。再选择这N-1类中距离最近的两类加以合 并,余下N-2类。依次类推。这样,每合并一次,就减少一 类,继续这一过程,直至将所有指标合并成为一类为止,形成 由小到大的分类系统,即谱系。最后整个分类结果画在一张图 上,称为聚类图或谱系图,以此直观地反映各指标间的亲疏关 系。 11.2.1.2 评价指标的选择方法

11.2.1.2评价指标的选择方法 第二种方法:聚类分析法 聚类分析法的具体实施步骤: ①选择度量指标间相似程度的方法。常用的方法是相关系数法。各指 标两两之间都可以计算相关系数,从而形成一个相关系数矩阵。 ②选择度量指标类间距离的方法。常用的方法有最长距离法、最短距 离法、重心法、类平均法、离差平方和法。由于一般利用相关系数表示指 标(类)间的相似程度,所以多采用相关系数量大法进行聚类。 ③根据聚类结果绘制聚类图。根据聚类结果确定指标体系,必须以相 关程度作为划分标准。至于分类时用的阈值为多少,要视对指标的简约性 要求不同而定。若对指标体系的简约性要求不高,可选择较高的相关系数 作为阈值,反之亦然。 ④根据最后划分的类别确定指标体系。由于同一类中指标的相似程度 相高,即信息重复较多,可以选择其中之一作为代表,从而达到简化指标 的目的
第二种方法:聚类分析法 聚类分析法的具体实施步骤: ①选择度量指标间相似程度的方法。常用的方法是相关系数法。各指 标两两之间都可以计算相关系数,从而形成一个相关系数矩阵。 ②选择度量指标类间距离的方法。常用的方法有最长距离法、最短距 离法、重心法、类平均法、离差平方和法。由于一般利用相关系数表示指 标(类)间的相似程度,所以多采用相关系数量大法进行聚类。 ③根据聚类结果绘制聚类图。根据聚类结果确定指标体系,必须以相 关程度作为划分标准。至于分类时用的阈值为多少,要视对指标的简约性 要求不同而定。若对指标体系的简约性要求不高,可选择较高的相关系数 作为阈值,反之亦然。 ④根据最后划分的类别确定指标体系。由于同一类中指标的相似程度 相高,即信息重复较多,可以选择其中之一作为代表,从而达到简化指标 的目的。 11.2.1.2 评价指标的选择方法
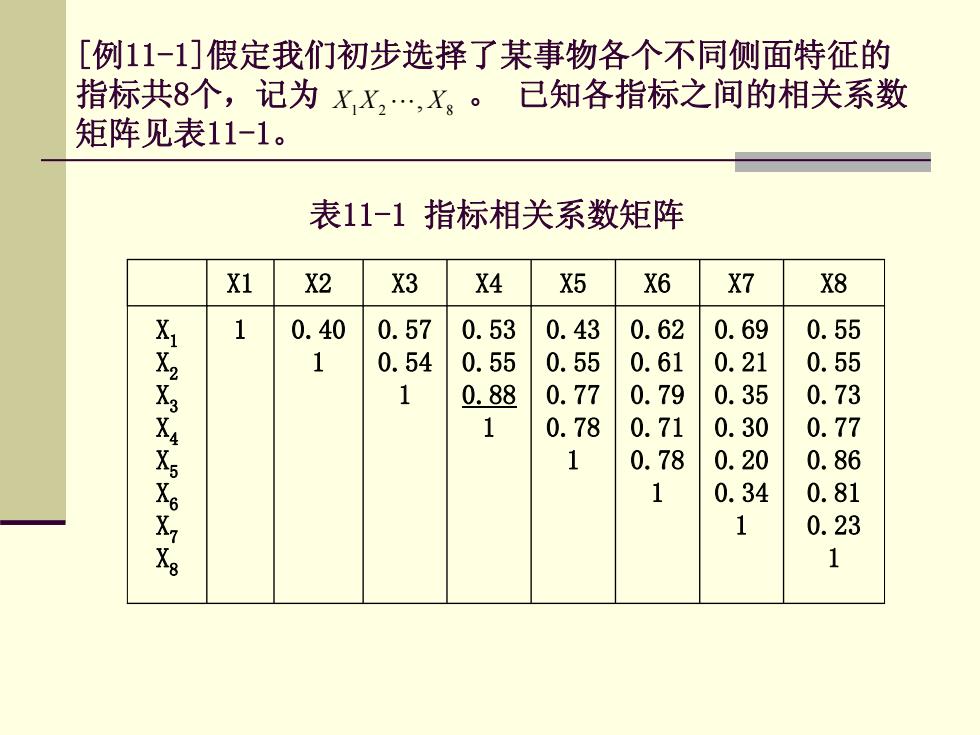
[例11-1]假定我们初步选择了某事物各个不同侧面特征的 指标共8个,记为X,X2,X。 已知各指标之间的相关系数 矩阵见表11-1。 表11-1指标相关系数矩阵 X1 X2 X3 X4 X5 X6 X7 X8 1 0.40 0.57 0.53 0.43 0.62 0.69 0.55 1 0.54 0.55 0.55 0.61 0.21 0.55 1 0.88 0.77 0.79 0.35 0.73 1 0.78 0.71 0.30 0.77 1 0.78 0.20 0.86 1 0.34 0.81 1 0.23 1
[例11-1]假定我们初步选择了某事物各个不同侧面特征的 指标共8个,记为 。 已知各指标之间的相关系数 矩阵见表11-1。 12 8 X X X L, 表11-1 指标相关系数矩阵 X1 X2 X3 X4 X5 X6 X7 X8 X1 X 2 X 3 X 4 X 5 X 6 X 7 X 8 1 0.40 1 0.57 0.54 1 0.53 0.55 0.88 1 0.43 0.55 0.77 0.78 1 0.62 0.61 0.79 0.71 0.78 1 0.69 0.21 0.35 0.30 0.20 0.34 1 0.55 0.55 0.73 0.77 0.86 0.81 0.23 1
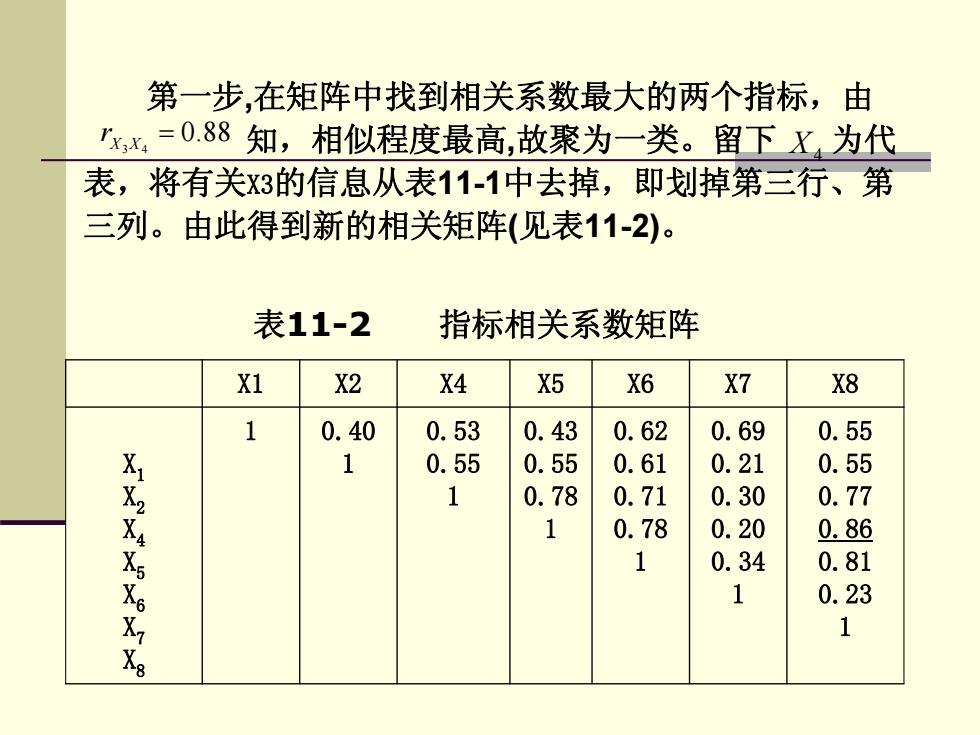
第一步,在矩阵中找到相关系数最大的两个指标,由 xx=0.88知,相似程度最高,故聚为一类。留下X为代 表,将有关3的信息从表11-1中去掉,即划掉第三行、第 三列。由此得到新的相关矩阵(见表11-2)。 表11-2 指标相关系数矩阵 X1 X2 X4 X5 X6 X7 X8 1 0.40 0.53 0.43 0.62 0.69 0.55 1 0.55 0.55 0.61 0.21 0.55 1 0.78 0.71 0.30 0.77 0.78 0.20 0.86 1 0.34 0.81 0.23 1
第一步,在矩阵中找到相关系数最大的两个指标,由 知,相似程度最高,故聚为一类。留下 为代 表,将有关X3的信息从表11-1中去掉,即划掉第三行、第 三列。由此得到新的相关矩阵(见表11-2)。 3 4 0.88 X X r = X4 X1 X2 X4 X5 X6 X7 X8 X1 X2 X4 X5 X6 X7 X8 1 0.40 1 0.53 0.55 1 0.43 0.55 0.78 1 0.62 0.61 0.71 0.78 1 0.69 0.21 0.30 0.20 0.34 1 0.55 0.55 0.77 0.86 0.81 0.23 1 表11-2 指标相关系数矩阵