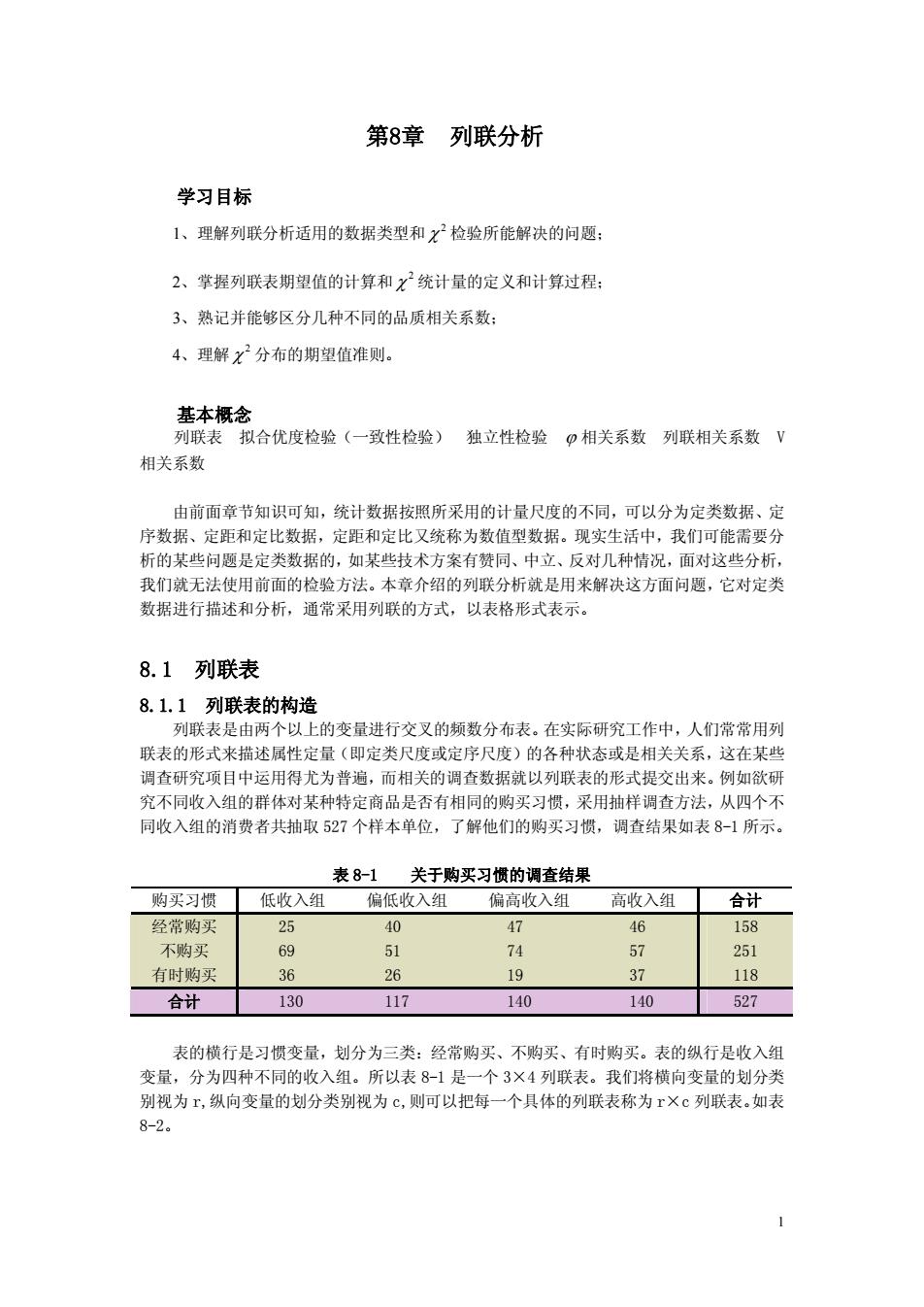
第8章列联分析 学习目标 1、理解列联分析适用的数据类型和x2检验所能解决的问题: 2、掌握列联表期望值的计算和X统计量的定义和计算过程: 3、熟记并能够区分几种不同的品质相关系数 4、理解X分布的期望值准则。 基太概念 列联表拟合优度检验(一致性检验)独立性检验口相关系数列联相关系数V 相关系数 由前面章节知识可知,统计数据按照所采用的计量尺度的不同,可以分为定类数据、定 序数据、定距和定比数据,定距和定比又统称为数值型数据。现实生活中,我们可能需要分 析的某些问题是定类数据的,如某些技术方案有赞同、中立、反对几种情况,面对这些分析 我们就无法使用前面的检验方法。本章介绍的列联分析就是用来解决这方面问题,它对定类 数据进行描述和分析,通常采用列联的方式,以表格形式表示。 8.1列联表 8.1.1列联表的构造 列联表是由两个以上的变量进行交叉的频数分布表。在实际研究工作中,人们常常用列 联表的形式来描述属性定量(即定类尺度或定序尺度)的各种状态或是相关关系,这在某些 调查研究项目中运用得尤为普遍,而相关的调查数据就以列联表的形式提交出来。例如欲研 究不同收入组的群体对某种特定商品是否有相同的购买习惯,采用抽样调杏方法,从四个不 同收入组的消费者共抽取527个样本单位, 了解他们的购买习惯,调查结果如表8-1所示。 表8-1 关于购买习惯的调查结果 购买习惯低收入组 偏低收入组偏高收入组 高收入组合计 经常购买 25 47 不购买 57 有时购买 36 26 19 37 118 合计 130 117 140 140 527 表的横行是习惯变量,划分为三类:经常购买、不购买、有时购买。表的纵行是收入组 变量,分为四种不同的收入组。所以表8-1是一个3×4列联表。我们将横向变量的划分类 别视为工,纵向变量的划分类别视为c,则可以把每一个具体的列联表称为r×c列联表.如表 8-2
1 第8章 列联分析 学习目标 1、理解列联分析适用的数据类型和 2 c 检验所能解决的问题; 2、掌握列联表期望值的计算和 2 c 统计量的定义和计算过程; 3、熟记并能够区分几种不同的品质相关系数; 4、理解 2 c 分布的期望值准则。 基本概念 列联表 拟合优度检验(一致性检验) 独立性检验 j 相关系数 列联相关系数 V 相关系数 由前面章节知识可知,统计数据按照所采用的计量尺度的不同,可以分为定类数据、定 序数据、定距和定比数据,定距和定比又统称为数值型数据。现实生活中,我们可能需要分 析的某些问题是定类数据的,如某些技术方案有赞同、中立、反对几种情况,面对这些分析, 我们就无法使用前面的检验方法。本章介绍的列联分析就是用来解决这方面问题,它对定类 数据进行描述和分析,通常采用列联的方式,以表格形式表示。 8.1 列联表 8.1.1 列联表的构造 列联表是由两个以上的变量进行交叉的频数分布表。 在实际研究工作中,人们常常用列 联表的形式来描述属性定量(即定类尺度或定序尺度)的各种状态或是相关关系,这在某些 调查研究项目中运用得尤为普遍,而相关的调查数据就以列联表的形式提交出来。例如欲研 究不同收入组的群体对某种特定商品是否有相同的购买习惯,采用抽样调查方法,从四个不 同收入组的消费者共抽取 527 个样本单位,了解他们的购买习惯,调查结果如表 8-1 所示。 表 8-1 关于购买习惯的调查结果 购买习惯 低收入组 偏低收入组 偏高收入组 高收入组 合计 经常购买 不购买 有时购买 25 40 47 46 69 51 74 57 36 26 19 37 158 251 118 合计 130 117 140 140 527 表的横行是习惯变量,划分为三类:经常购买、不购买、有时购买。表的纵行是收入组 变量,分为四种不同的收入组。所以表 8-1 是一个 3×4 列联表。我们将横向变量的划分类 别视为 r,纵向变量的划分类别视为 c,则可以把每一个具体的列联表称为 r×c 列联表。 如表 8-2
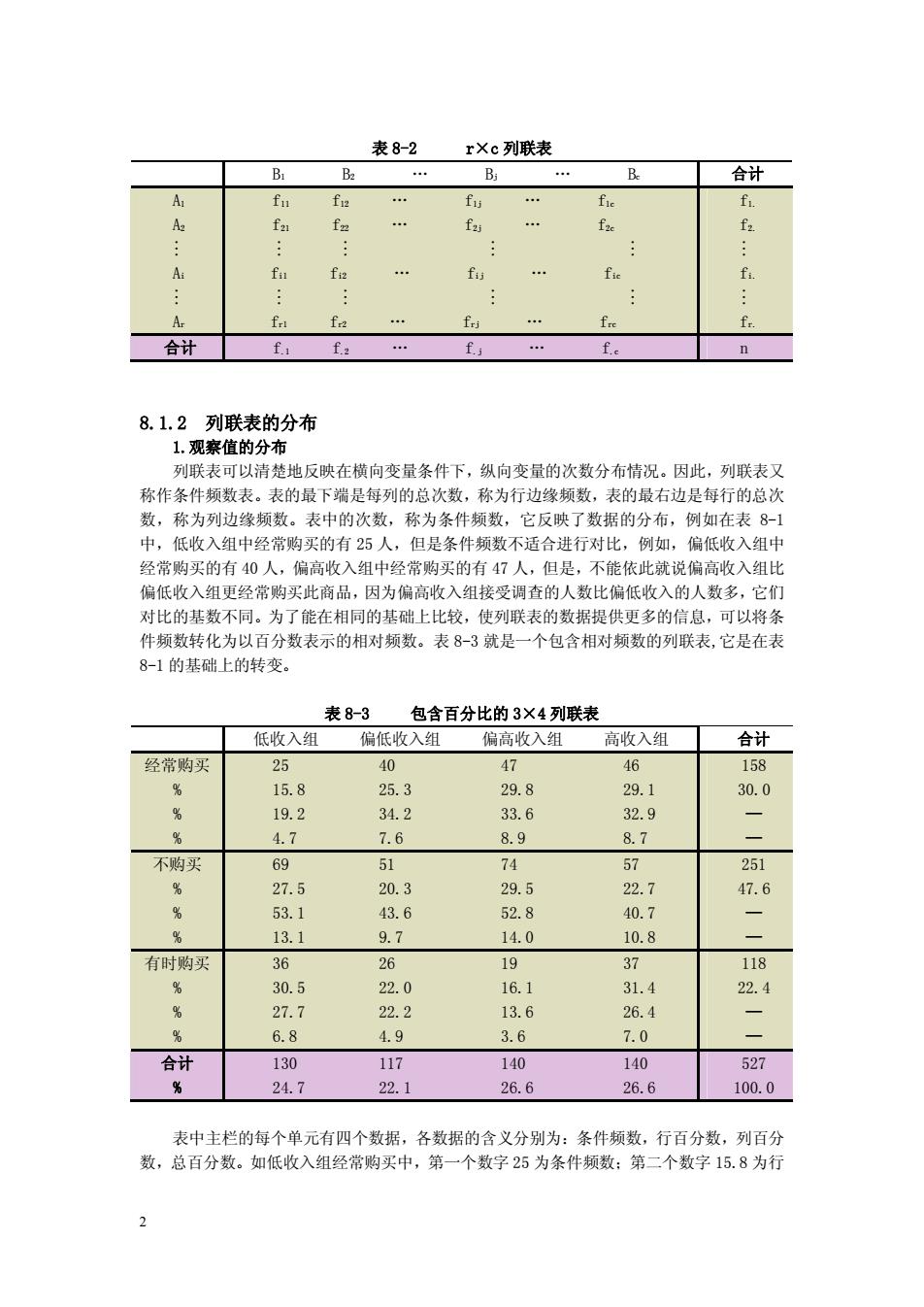
表8-2 rXc列联表 B 合计 f f f fa 合计 fa f f 8.1.2列联表的分布 1观察值的分布 列联表可以清楚地反映在横向变量条件下,纵向变量的次数分布情况。因此,列联表又 称作条件须数表。表的最下端是每列的总次数,称为行边缘频数,表的最右边是每行的总 数,称为列边缘频数。表中的次数,称为条件频数,它反映了数据的分布,例如在表8-1 中,低收入组中经常购买的有25人,但是条件频数不适合进行对比,例如,偏低收入组中 经常购买的有40人,偏高收入组中经常购买的有47人,但是,不能依此就说偏高收入组比 偏低收入组更经常购买此商品,因为偏高收入组接受调查的人数比偏低收入的人数多,它们 对比的基数不同。为了能在相同的基础上比较,使列联表的数据提供更多的信息,可以将条 件烦数转化为以百分数表示的相对烦数。表8-3就是一个包含相对顿数的列联表,它是在表 8-1的基础上的转变。 表8-3 包含百分比的3×4列联表 低收入组 偏低收入组 偏高收入组 高收入组 合计 经常购买 25 40 47 46 158 158 253 208 2g1 30.0 192 3492 336 32.9 4.7 7.6 89 8.7 不购买 69 51 74 吟 251 275 203 29.5 227 47.6 53.1 43.6 528 40.7 13.1 9.7 14.0 10.8 有时购买 36 26 19 37 118 30.5 22.0 16.1 31.4 22.4 27.7 22.2 13.6 26.4 6.8 4.9 3.6 7.0 合计 130 117 140 140 527 24.7 22.1 26.6 26.6 100.0 表中主栏的每个单元有四个数据,各数据的含义分别为:条件频数,行百分数,列百分 数,总百分数。如低收入组经常购买中,第一个数字25为条件频数:第二个数字15.8为行
2 表 8-2 r×c 列联表 B1 B2 . Bj . Bc 合计 A1 A2 M Ai M Ar f11 f12 . f1j . f1c f21 f22 . f2j . f2c M M M M fi1 fi2 . fij . fic M M M M fr1 fr2 . frj . frc f1. f2. M fi. M fr. 合计 f.1 f.2 . f.j . f.c n 8.1.2 列联表的分布 1.观察值的分布 列联表可以清楚地反映在横向变量条件下,纵向变量的次数分布情况。因此,列联表又 称作条件频数表。表的最下端是每列的总次数,称为行边缘频数,表的最右边是每行的总次 数,称为列边缘频数。表中的次数,称为条件频数,它反映了数据的分布,例如在表 8-1 中,低收入组中经常购买的有 25 人,但是条件频数不适合进行对比,例如,偏低收入组中 经常购买的有 40 人,偏高收入组中经常购买的有 47 人,但是,不能依此就说偏高收入组比 偏低收入组更经常购买此商品, 因为偏高收入组接受调查的人数比偏低收入的人数多,它们 对比的基数不同。为了能在相同的基础上比较,使列联表的数据提供更多的信息,可以将条 件频数转化为以百分数表示的相对频数。表 8-3 就是一个包含相对频数的列联表,它是在表 8-1 的基础上的转变。 表 8-3 包含百分比的 3×4 列联表 低收入组 偏低收入组 偏高收入组 高收入组 合计 经常购买 % % % 25 40 47 46 15.8 25.3 29.8 29.1 19.2 34.2 33.6 32.9 4.7 7.6 8.9 8.7 158 30.0 — — 不购买 % % % 69 51 74 57 27.5 20.3 29.5 22.7 53.1 43.6 52.8 40.7 13.1 9.7 14.0 10.8 251 47.6 — — 有时购买 % % % 36 26 19 37 30.5 22.0 16.1 31.4 27.7 22.2 13.6 26.4 6.8 4.9 3.6 7.0 118 22.4 — — 合计 % 130 117 140 140 24.7 22.1 26.6 26.6 527 100.0 表中主栏的每个单元有四个数据,各数据的含义分别为:条件频数,行百分数,列百分 数,总百分数。如低收入组经常购买中,第一个数字 25 为条件频数;第二个数字 15.8 为行

百分数,即25/158=15.8%:第三个数字19.2为列百分数,即25/130=19.2%:第四个数字 4.7为总百分数,即25/527=4.7%。在最右边和最下边的合计栏中各有两行数据,第一行是 边缘频数,第二行是边缘频数的百分数。如最右边的30.0%158/527,最下边的24.7%=130/ 527。这里我们分析的是观察值的分布,但是仅仅依赖这些还难以进行深入的分析,为此我 们引入期型分布的概念。 2.期望值的分布 仍以前例为例。在全部527个总体中,经常购买的有158个,占总数的30.0%,但我们 希望了解各收入组购买习惯是否存在差异。如果各收入组的购买习惯相同,那么对于低收入 组中经常购买的人数应当为130×30.0%39人,偏低收入组中经常购买的人数应当为117 30%=35人,这39人和35人就是本例中的期望值。按此计算可得各个单元期望值的分布, 如表8-4。 表8-4期望值分布表 低收入 偏低收入组 偏高收入组 高收入组 0.300 0.300 0.300 0.300 经常购买的 130 ×117 ×140 140 期望值 39 35 49 42 0.476 0.476 0.476 0.476 不购买的 ×130 X117 ×140 ×140 期望值 62 56 67 67 有时购买的 0.224 0.224 0.224 0.224 130 117 140 140 期型值 29 26 31 31 观察值和期望值分布得出后,接下来对列联表中的变量进行分析,这时可以采用统计分 析方法。列联表分析的统计分析方法很多,除了Pearson检验、校正X2检验、Fisher 的精确检验外,还有秩和检验、Ridit分析、对应分析、Kappa检验等。由于分析方法繁多 且复杂,本书仅说明实际中适用范围最广的X检验。 82x分布与x检验 8.2.1x分布 X分布是在统计学中经常用到的一种统计分布。假设X,X,·,X。是n个相互独立 的随机变量,且X,口N(0,1),1=1,2,.,n,那么我们就定义X=X2+X,2+.+X2服 从自由度为n的x2分布,记作X口x2(n) 8.2.2x2统计量 3
3 百分数,即 25/158=15.8%;第三个数字 19.2 为列百分数,即 25/130=19.2%;第四个数字 4.7 为总百分数,即 25/527=4.7%。在最右边和最下边的合计栏中各有两行数据,第一行是 边缘频数,第二行是边缘频数的百分数。如最右边的 30.0%=158/527,最下边的 24.7%=130/ 527。这里我们分析的是观察值的分布,但是仅仅依赖这些还难以进行深入的分析,为此我 们引入期望分布的概念。 2.期望值的分布 仍以前例为例。在全部 527 个总体中,经常购买的有 158 个,占总数的 30.0%,但我们 希望了解各收入组购买习惯是否存在差异。如果各收入组的购买习惯相同, 那么对于低收入 组中经常购买的人数应当为 130×30.0%=39 人,偏低收入组中经常购买的人数应当为 117× 30%=35 人,这 39 人和 35 人就是本例中的期望值。按此计算可得各个单元期望值的分布, 如表 8-4。 表 8-4 期望值分布表 低收入组 偏低收入组 偏高收入组 高收入组 经常购买的 期望值 0.300 × 130 39 0.300 × 117 35 0.300 × 140 42 0.300 × 140 42 不购买的 期望值 0.476 × 130 62 0.476 × 117 56 0.476 × 140 67 0.476 × 140 67 有时购买的 期望值 0.224 × 130 29 0.224 × 117 26 0.224 × 140 31 0.224 × 140 31 观察值和期望值分布得出后,接下来对列联表中的变量进行分析, 这时可以采用统计分 析方法。列联表分析的统计分析方法很多,除了 Pearson 2 c 检验、校正 2 c 检验、Fisher 的精确检验外,还有秩和检验、Ridit 分析、对应分析、Kappa 检验等。由于分析方法繁多 且复杂,本书仅说明实际中适用范围最广的 2 c 检验。 8.2 2 c 分布与 2 c 检验 8.2.1 2 c 分布 2 c 分布是在统计学中经常用到的一种统计分布。假设 1 2 , , X X ., Xn 是 n 个相互独立 的随机变量,且 Xi : N (0,1) ,i =1,2,. , n ,那么我们就定义 2 2 2 X = X1 + X2 +. + Xn 服 从自由度为n 的 2 c 分布,记作 2 X : c (n) 。 8.2.2 2 c 统计量
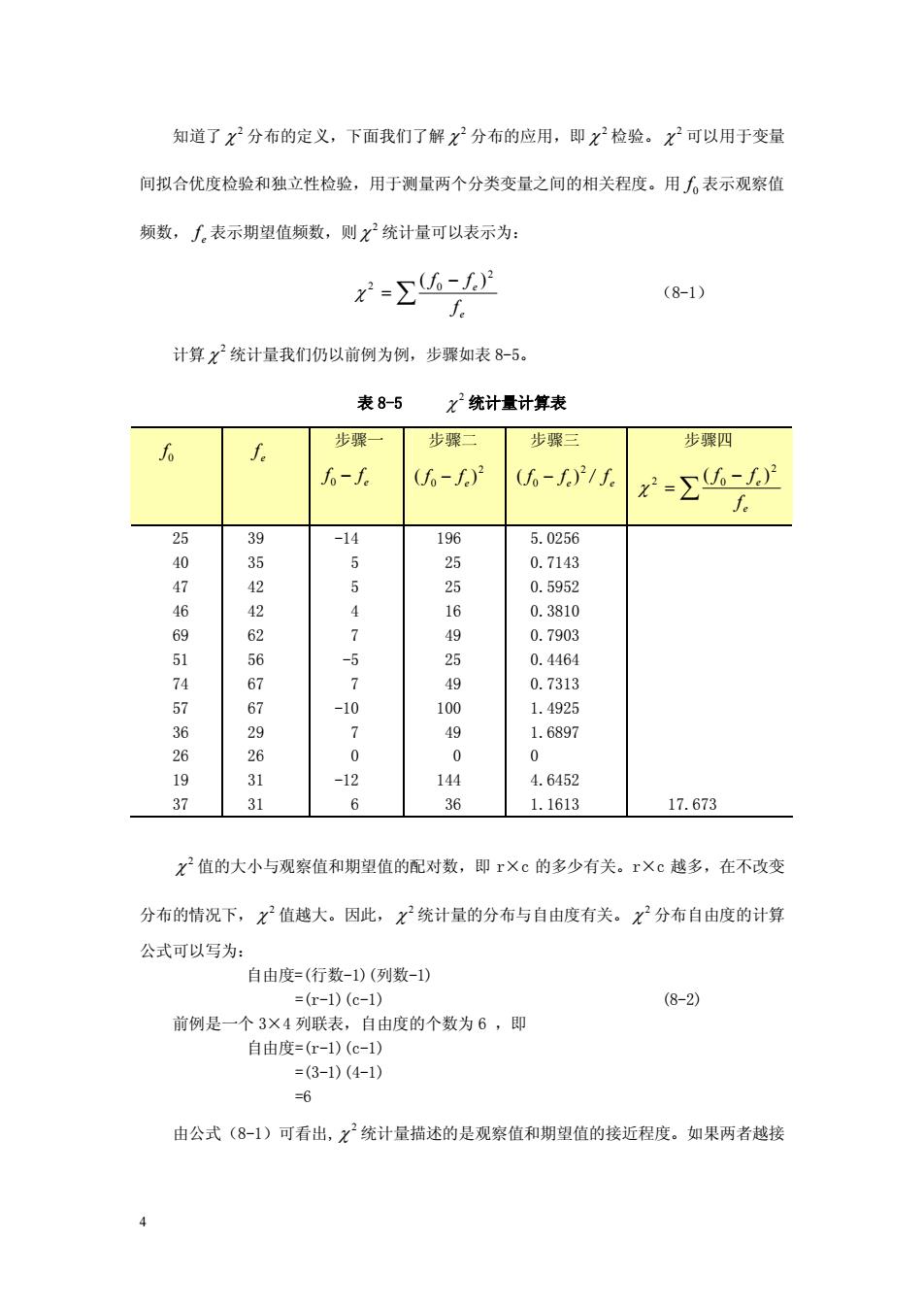
知道了x分布的定义,下面我们了解父2分布的应用,即x检验。X2可以用于变量 间拟合优度检验和独立性检验,用于测量两个分类变量之间的相关程度。用表示观察值 频数,∫。表示期望值频数,则x统计量可以表示为: =∑6- (8-1) f。 计算义己统计量我们仍以前例为例,步骤如表8-5。 表8-5 x统计量计算表 步骤一 步骤二 步骤三 步强四 fo-f (6-) -)21f x=∑- 25 39 -14 196 5.0256 35 0.7143 47 42 0.5952 0.3810 62 7 0.7903 -5 24 0.446 0.7313 67 100 1.4925 7 1.6897 名 26 0 0 0 19 31 -12 144 4.6452 37 31 6 36 1.1613 17.673 X值的大小与观察值和期望值的配对数,即r×c的多少有关。r×c越多,在不改变 分布的情况下,X值越大。因此,X统计最的分布与自由度有关。X分布自由度的计算 公式可以写为: 自由度=(行数-1)(列数-1) =r-1)(c-1) (8-2) 前例是一个3×4列联表,自由度的个数为6,即 自由度=(r-1)(c-1) =(3-1)(4-1 6 由公式(8-1)可看出,X统计量描述的是观察值和期望值的接近程度。如果两者越接
4 知道了 2 c 分布的定义,下面我们了解 2 c 分布的应用,即 2 c 检验。 2 c 可以用于变量 间拟合优度检验和独立性检验,用于测量两个分类变量之间的相关程度。用 0 f 表示观察值 频数, e f 表示期望值频数,则 2 c 统计量可以表示为: Â - = e e f f f 2 2 0 ( ) c (8-1) 计算 2 c 统计量我们仍以前例为例,步骤如表 8-5。 表 8-5 2 c 统计量计算表 0 f e f 步骤一 e f - f 0 步骤二 2 0 ( ) e f - f 步骤三 2 0 ( ) e f - f / e f 步骤四 Â - = e e f f f 2 2 0 ( ) c 25 40 47 46 69 51 74 57 36 26 19 37 39 35 42 42 62 56 67 67 29 26 31 31 -14 5 5 4 7 -5 7 -10 7 0 -12 6 196 25 25 16 49 25 49 100 49 0 144 36 5.0256 0.7143 0.5952 0.3810 0.7903 0.4464 0.7313 1.4925 1.6897 0 4.6452 1.1613 17.673 2 c 值的大小与观察值和期望值的配对数,即 r×c 的多少有关。r×c 越多,在不改变 分布的情况下, 2 c 值越大。因此, 2 c 统计量的分布与自由度有关。 2 c 分布自由度的计算 公式可以写为: 自由度=(行数-1)(列数-1) =(r-1)(c-1) (8-2) 前例是一个 3×4 列联表,自由度的个数为 6 ,即 自由度=(r-1)(c-1) =(3-1)(4-1) =6 由公式(8-1)可看出, 2 c 统计量描述的是观察值和期望值的接近程度。如果两者越接

近,即。-的绝对值越小,计算出的x越小:反之,如果。-f的绝对值越大,计算 出的越大。X检验正是运用X的计算结果与X分布中的临界值进行比较,做出对原 假设接受或拒绝的统计决策。 8.2.3X2检验 x2统计量是由皮尔逊(Pearson)引入的,故我们也叫它皮尔逊统计量,其实按式(8-1) 定义的函数自身并不服从x2分布,但是皮尔逊证明了它的极限分布为X分布。在应用中, 只要样本量充分大时,X统计量渐近地服从X分布,因此我们可以就其进行检验, 根据列联表的不同内容,可以进行拟合优度检验(一致性检验)和独立性检验。从表面 上看,一致性检验和独立性检验不论在列联表的形式上,还是在计算x的公式上都是相同 的,所以经常被笼统地称为X检验。但是两者还是存在差异的。 首先,两种检验抽取样本的方法不同。如果抽样是在各类别中分别进行,依照各类别分 别计算其比例,则属于拟合优度检验。如果抽样时并未事先分类,抽样后根据研究内容,把 入选单位按两类变量进行分类,形成列联表,则是独立性检验。 其次,两种检验假设的内容有所差异。对于拟合优度检验,原假设通常是假设个类别总 体比例等于某个期望概率,而独立性检验中原假设则假设两个变量之间独立。 最后,期望频数的计算 在拟合优度检验中是利用原假设中的期望概率,用观察频数乘 以期望概率,直接得到期望须数独立性检验中两个水平的联合概率是两个单独概率的乘积。 1,拟合优度检验 如果样本是从总体的不同类别中分别抽取,研究目的是对不同类别的目标量之间是否存 在显艺性差异讲行检验,我们就把它称为拟合优度检验,在某些书上也叫做一致性检验。前 面举的例子中,如果我们要检验四个收入组中购买习惯是否一致,就是要检验在不同的购买 习惯上比例是否一致,下边我们将其作为 一个例子来了解拟合优度检验 [例81]欲研究不同收入群体对某种特定商品是否有相同的购买习惯,市场调查人员 调查了四个不同收入组的消费者共527人,购买习惯分为:经常购买、不购买、有时购买。 调查结果如表8-1,以ā=0.1的显著性水平检验不同收入群体中的购买习惯是否存在差异。 :如果不存在差异,四个收入水平的购买习惯应该是一致的,所以原假设和备选假设 分别为 Hh:Pi=P:=P=P4 H:P、P、P、P不全相等 由式(8-1)得 2=Σ6-D1.6m3 由式(8-2)得 自由度=(r-1)(c-1)=(3-1)(4-1)=6 因为a=0.1,查表得x6:(6)=10.645。由于x2>x2,故拒绝原假设,即认为不同收 5
5 近,即 e f - f 0 的绝对值越小,计算出的 2 c 越小;反之,如果 e f - f 0 的绝对值越大,计算 出的 2 c 越大。 2 c 检验正是运用 2 c 的计算结果与 2 c 分布中的临界值进行比较,做出对原 假设接受或拒绝的统计决策。 8.2.3 2 c 检验 2 c 统计量是由皮尔逊 (Pearson) 引入的, 故我们也叫它皮尔逊统计量, 其实按式 (8-1) 定义的函数自身并不服从 2 c 分布,但是皮尔逊证明了它的极限分布为 2 c 分布。在应用中, 只要样本量充分大时, 2 c 统计量渐近地服从 2 c 分布,因此我们可以就其进行 2 c 检验。 根据列联表的不同内容,可以进行拟合优度检验(一致性检验)和独立性检验。从表面 上看,一致性检验和独立性检验不论在列联表的形式上,还是在计算 2 c 的公式上都是相同 的,所以经常被笼统地称为 2 c 检验。但是两者还是存在差异的。 首先,两种检验抽取样本的方法不同。如果抽样是在各类别中分别进行,依照各类别分 别计算其比例,则属于拟合优度检验。如果抽样时并未事先分类,抽样后根据研究内容,把 入选单位按两类变量进行分类,形成列联表,则是独立性检验。 其次,两种检验假设的内容有所差异。对于拟合优度检验,原假设通常是假设个类别总 体比例等于某个期望概率,而独立性检验中原假设则假设两个变量之间独立。 最后,期望频数的计算。在拟合优度检验中是利用原假设中的期望概率,用观察频数乘 以期望概率, 直接得到期望频数。 独立性检验中两个水平的联合概率是两个单独概率的乘积。 1.拟合优度检验 如果样本是从总体的不同类别中分别抽取, 研究目的是对不同类别的目标量之间是否存 在显著性差异进行检验,我们就把它称为拟合优度检验,在某些书上也叫做一致性检验。前 面举的例子中,如果我们要检验四个收入组中购买习惯是否一致, 就是要检验在不同的购买 习惯上比例是否一致,下边我们将其作为一个例子来了解拟合优度检验。 [例 8-1 ]欲研究不同收入群体对某种特定商品是否有相同的购买习惯,市场调查人员 调查了四个不同收入组的消费者共 527 人,购买习惯分为:经常购买、不购买、有时购买。 调查结果如表 8-1,以α=0.1 的显著性水平检验不同收入群体中的购买习惯是否存在差异。 解:如果不存在差异,四个收入水平的购买习惯应该是一致的,所以原假设和备选假设 分别为: H0: P1=P2 =P3=P4; H1: P1、P2 、P3、P4不全相等 由式(8-1)得 Â - = e e f f f 2 2 0 ( ) c =17.673 由式(8-2)得 自由度=(r-1)(c-1)=(3-1)(4-1)=6 因为α=0.1,查表得 (6) 10. 645 2 c 0. 1 = 。由于 2 2 c > c a ,故拒绝原假设,即认为不同收