傅立叶级数三角函数形式: aeos吧+b,n (n=0,1,2,.) nπX ran=∫fx)cos"吧dk, n= (m=1,2,3…) 傅立叶级数复数形式: f)=∑ce晋 ● a=f)e学a( m=0,±1,±2,…) n=-00 回学+日学: 实函数
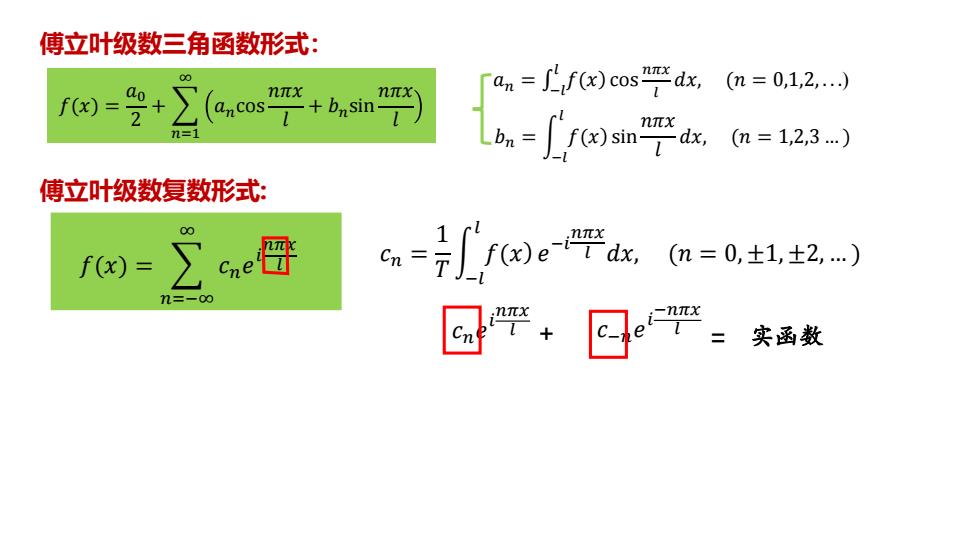
𝑓(𝑥) = 𝑎0 2 + 𝑛=1 ∞ 𝑎𝑛cos 𝑛𝜋𝑥 𝑙 + 𝑏𝑛sin 𝑛𝜋𝑥 𝑙 ��− = �𝑎� 𝑙 𝑓(𝑥) cos 𝑛𝜋𝑥 𝑙 𝑑𝑥, (𝑛 = 0,1,2, . . .) 𝑏𝑛 = න −𝑙 𝑙 𝑓(𝑥) sin 𝑛𝜋𝑥 𝑙 𝑑𝑥, (𝑛 = 1,2,3 … ) 傅立叶级数三角函数形式: 傅立叶级数复数形式: 𝑓(𝑥) = 𝑛=−∞ ∞ 𝑐𝑛𝑒 𝑖 𝑛𝜋𝑥 𝑙 𝑐𝑛 = 1 𝑇 න −𝑙 𝑙 𝑓(𝑥) 𝑒 −𝑖 𝑛𝜋𝑥 𝑙 𝑑𝑥, (𝑛 = 0, ±1, ±2, … ) 𝑐𝑛𝑒 𝑖 𝑛𝜋𝑥 𝑙 𝑐−𝑛𝑒 𝑖 −𝑛𝜋𝑥 + 𝑙 = 实函数
傅立叶级数三角函数形式: 00 an=∫f)cos"吧dx,m=01,2) f(x)= πx ancos-I +bnsin-I n= 6=fsn'ka=123-) 傅立叶级数复数形式: 00 f(x)= c=r网e学xa=0士,t2-) =-00 Imag(j) Real -3 -2 3
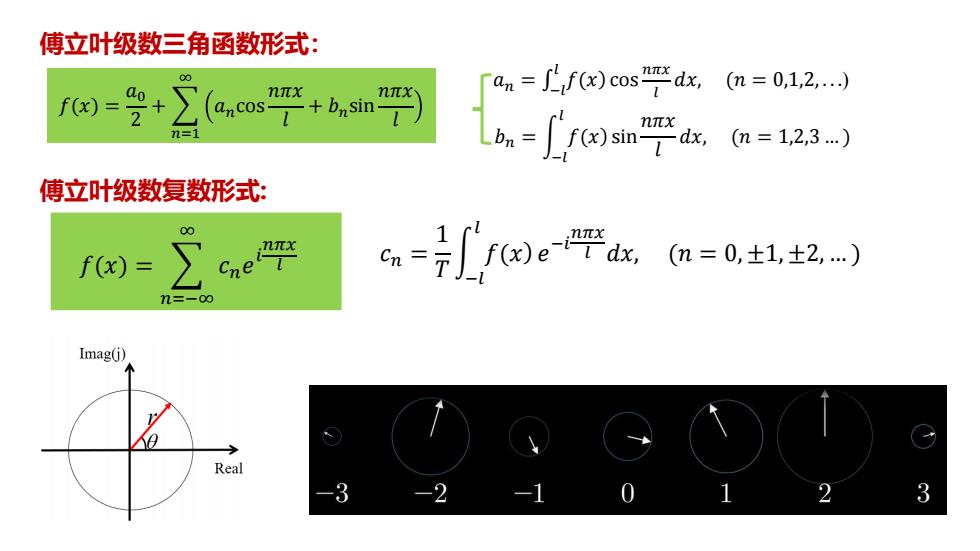
𝑓(𝑥) = 𝑎0 2 + 𝑛=1 ∞ 𝑎𝑛cos 𝑛𝜋𝑥 𝑙 + 𝑏𝑛sin 𝑛𝜋𝑥 𝑙 ��− = �𝑎� 𝑙 𝑓(𝑥) cos 𝑛𝜋𝑥 𝑙 𝑑𝑥, (𝑛 = 0,1,2, . . .) 𝑏𝑛 = න −𝑙 𝑙 𝑓(𝑥) sin 𝑛𝜋𝑥 𝑙 𝑑𝑥, (𝑛 = 1,2,3 … ) 傅立叶级数三角函数形式: 傅立叶级数复数形式: 𝑓(𝑥) = 𝑛=−∞ ∞ 𝑐𝑛𝑒 𝑖 𝑛𝜋𝑥 𝑙 𝑐𝑛 = 1 𝑇 න −𝑙 𝑙 𝑓(𝑥) 𝑒 −𝑖 𝑛𝜋𝑥 𝑙 𝑑𝑥, (𝑛 = 0, ±1, ±2, … )