
主要内容 图像退化/复原过程的模型 ·噪声模型 ·空间域滤波方法 •频率域滤波方法 ·退化函数的估计 ·逆滤波 ·维纳滤波
主要内容 • 图像退化/复原过程的模型 • 噪声模型 • 空间域滤波方法 • 频率域滤波方法 • 退化函数的估计 • 逆滤波 • 维纳滤波
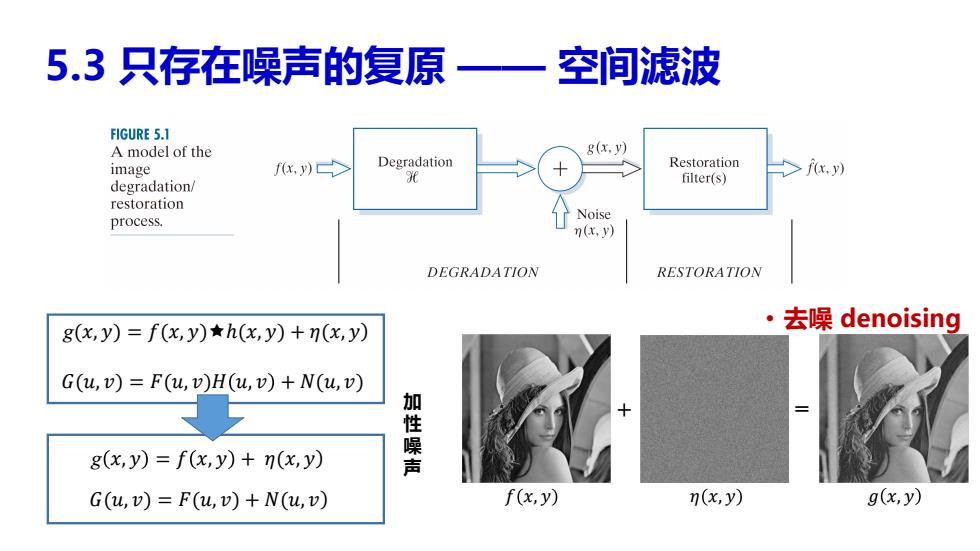
5.3只存在噪声的复原 一空间滤波 FIGURE 5.1 A model of the 8(x,y) image f(x,y) Degradation Restoration 9光 >f(r.y) filter(s) degradation/ restoration process. Noise n(x.y) DEGRADATION RESTORATION g(x,y)=f(x,y)h(x,y)+n(x,y) ·去噪denoising G(u,v)=F(u,v)H(u,v)+N(u,v) g(x,y)=f(x,y)+n(x,y) 加性噪声 G(u,)=F(u,)+N(u,v) f(x,y) n(x,y) g(x,y)
5.3 只存在噪声的复原 —— 空间滤波 g(𝑥, 𝑦ሻ = 𝑓(𝑥, 𝑦ሻℎ(𝑥, 𝑦ሻ + 𝜂(𝑥, 𝑦ሻ 𝐺(𝑢, 𝑣ሻ = 𝐹(𝑢, 𝑣ሻ𝐻 𝑢, 𝑣 + 𝑁(𝑢, 𝑣ሻ g 𝑥, 𝑦 = 𝑓 𝑥, 𝑦 + 𝜂(𝑥, 𝑦ሻ 𝐺(𝑢, 𝑣ሻ = 𝐹(𝑢, 𝑣ሻ + 𝑁(𝑢, 𝑣ሻ 加 性 噪 声 • 去噪 denoising + = 𝑓 𝑥, 𝑦 𝜂 𝑥, 𝑦 𝑔 𝑥, 𝑦

图像降噪一噪声图像相加(平均) 8(x,y)=f(x,y)+7(x,y) 退化的图像 理想图像 噪声 假设噪声服从零均值的高斯分布7x,y)小N(0,Ox) 输入同一物体的K副图像8,(x,y),i=1,2,…,K 输出国像为8(x,川=K立8(化,川 期里E{8(x,)}=f(Gx,)方差 o 1 2 (x,y) K n(x,y)
退化的图像 理想图像 噪声 输入同一物体的K副图像 输出图像为 期望 方差 图像降噪 —— 噪声图像相加(平均) g x y f x y x y ( , ) ( , ) ( , ) 假设噪声服从零均值的高斯分布 2 ( , ) ( , )~ (0, ) x y x y N ( , ), 1,2, , i g x y i K 1 1 ( , ) ( , ) K i i g x y g x y K E g x y f x y ( , ) ( , ) 2 2 ( , ) ( , ) 1 g x y = x y K = +
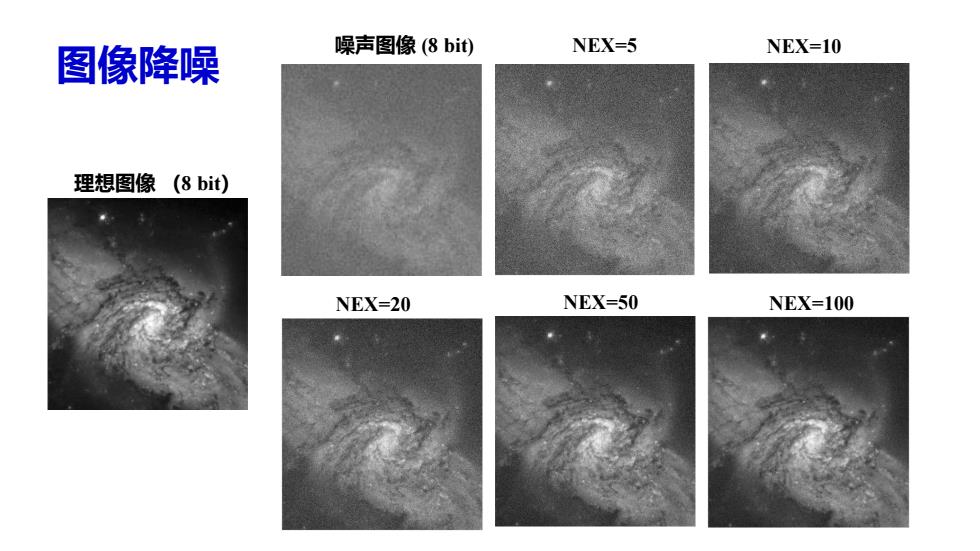
图像降噪 噪声图像(8bi0 NEX=5 NEX=10 理想图像(8bit) NEX=20 NEX-50 NEX=100
噪声图像 (8 bit) NEX=5 NEX=10 NEX=20 NEX=50 NEX=100 理想图像 (8 bit) 图像降噪

1=100,o=10
I=100, 10