
解:m=1kg,C02(g) T1=300K=0T2=800K (1)平均摩尔定压热容的定义为 Ca=CdrT,-T) Com/(Jmol-.K-1)=126.75+42.258×10-3(TK)-14.25 ×10-6(T/K)21dT/(T2-T1) =26.75×(800-300)+42.258×10-3× (8002-3002)2-14.25×10-6× (8003-3003)31/(800-300) =45.384 所以 Co.m=45.384 J.mol-1.K-1 (2)M(C02)=44.01×10-3 kg"mol1 Q=nCp.m(T2-T1) ={1kg/八44.01×10-3kg"mol-1)月×45.384Jmol1.K-1 ×(800-300)K =515.6kJ 2.7容积为0.1m的恒容密闭容器中有一绝热隔板,其两侧分别为0℃,4mo1的Ar(g)及150℃,2mol 的Cu(s)。现将隔板撤掉,整个系统达到热平衡,求末态温度t及过程的△H。已知:Ar(g)和Cu(s)的 摩尔定压热容C分别为20.786J·mol1.K及24.435J·mol1,K1,且假设均不随温度而变。 解:图示如下 Ar(g) Cu(s) Ar(g) Cu(s) n =4 mol 1=2m0 n=4 mol 2 mol T=0 =1509 假设:绝热壁与铜块紧密接触,且铜块的体积随温度的变化可忽略不计 则该过程可看作恒容过程,因 n(Ar.g)Cyn (Ar.g)-t(Ar.g)]=n(Cu,s)Cy.n (Cu,s)(Cu.s)-t] n(Cu,s)Cv.(Cu,s(Cu,s) f= n(Ar.g)Cvn(Ar.g)+n(Cu.s)Cy.n (Cu.s) 2×24.435×150 4×20786-8314+2x24457423C
2.7 容积为 0.1 m 3的恒容密闭容器中有一绝热隔板,其两侧分别为 0℃,4 mol 的 Ar(g)及 150℃,2 mol 的 Cu(s)。现将隔板撤掉,整个系统达到热平衡,求末态温度 t 及过程的 。已知:Ar(g)和 Cu(s)的 摩尔定压热容 分别为 及 ,且假设均不随温度而变。 解:图示如下 假设:绝热壁与铜块紧密接触,且铜块的体积随温度的变化可忽略不计 则该过程可看作恒容过程,因 此

假设气体可看作理想气体,Ca(Ou,)≈C=(C,司,则 △H=n(Ar,g)C,n△t+n(Cu,sCvn△t =4×20.784×74.23-0)+2×24.435×150-74.23) =2.47k 2.8单原子理想气体A与双原子理想气体B的混合物共5mo1,摩尔分数少=04,始态温度买=400K, 压力P=200kPa。今该混合气体绝热反抗恒外压D=100kPa膨胀到平衡态。求末态温度乃及过程的 W,△U,△H 解:过程图示如下 A+B A+B =3 mol adlbedlo =3m0 电=2m0 =400k o吐邦e=100h =200kP PI=100 kPa 分析:因为是绝热过程,过程热力学能的变化等于系统与环境间以功的 形势所交换的能量。因此, AU=-paAV=nACy(A)+ngCyn (B)AT 单原子分子一号8,双原子分千8 ]H-动 1g-5+2-号斯-刊 P1 会鄂作x 由于对理想气体和H均只是温度的函数,所以
假设气体可看作理想气体, ,则 2.8 单原子理想气体 A 与双原子理想气体 B 的混合物共 5 mol,摩尔分数 ,始态温度 , 压力 。今该混合气体绝热反抗恒外压 膨胀到平衡态。求末态温度 及过程的 。 解:过程图示如下 分析:因为是绝热过程,过程热力学能的变化等于系统与环境间以功的 形势所交换的能量。因此, 单原子分子 ,双原子分子 由于对理想气体 U 和 H 均只是温度的函数,所以
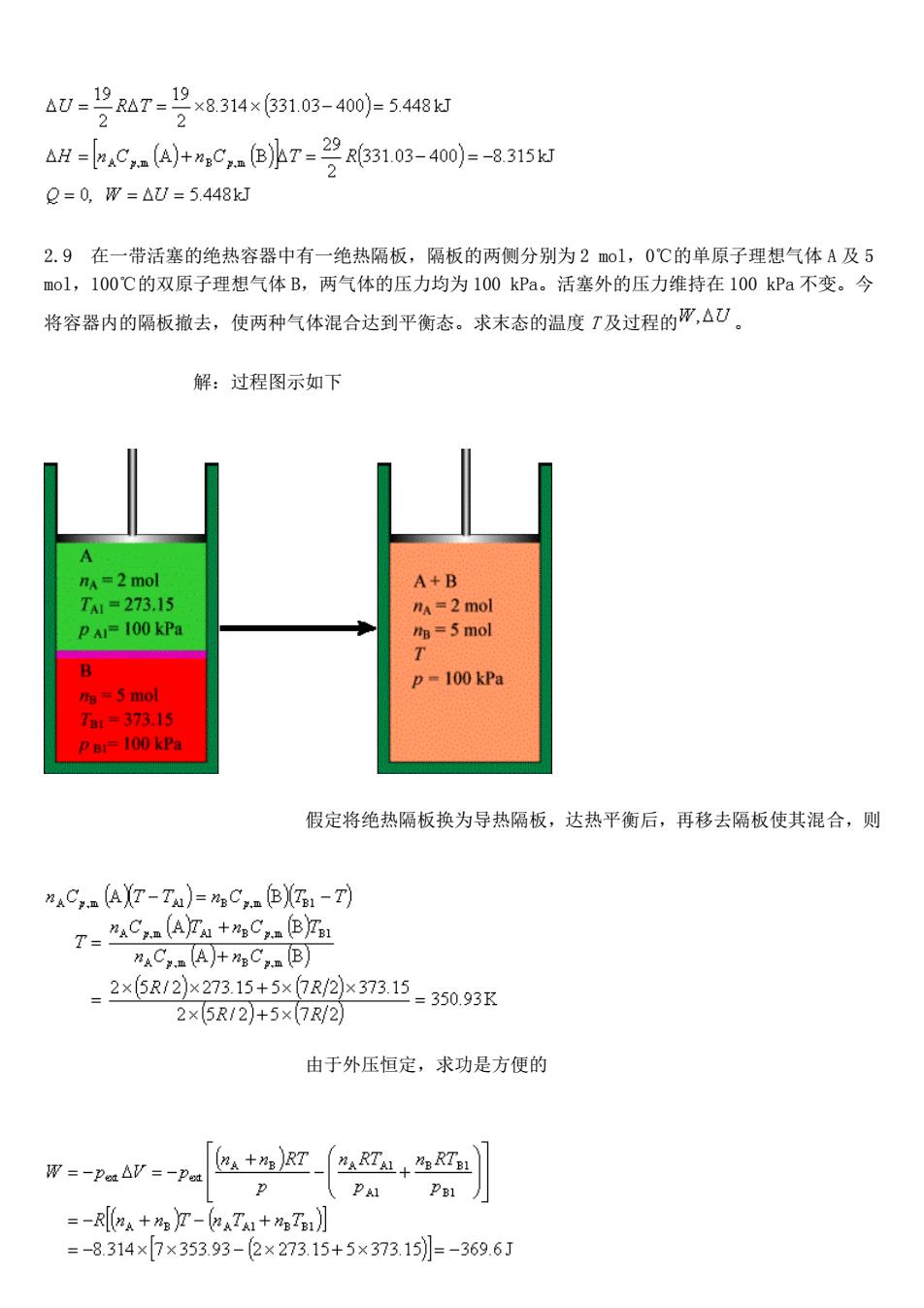
△U=9R△7=-12×8.314×631.03-40))=548 2 △H-,C)+a,C.色lr-2063103-40j=-8315u 2=0,W=△0=5.448k 2.9在一带活塞的绝热容器中有一绝热隔板,隔板的两侧分别为2mo1,0℃的单原子理想气体A及5 mol,100℃的双原子理想气体B,两气体的压力均为100kPa。活塞外的压力维持在100kPa不变。今 将容器内的隔板撒去,使两种气体混合达到平衡态。求末态的温度T及过程的印,△U。 解:过程图示如下 A =2 mol A+B T=273.15 A=2 mol B=5 mol D-100 kPa ta=5 mol 137315 P BI=100 kPa 假定将绝热隔板换为导热隔板,达热平衡后,再移去隔板使其混合,则 AC-(AXT-TA)=mC,(BXT-T) T-C AYA+C,_®jrL naC,.(A)+nC.n (B) -2x5R/2x273.15+5xR2373.15-350.93r 2×5R12)+5×7R/2 由于外压恒定,求功是方便的 W=-Pam△/=-Pea +R辽R丛+R】 、P =-R8A+T-(a4TA1+T】 =-8.314×7×353.93-(2×273.15+5×373.15=-369.6J
2.9 在一带活塞的绝热容器中有一绝热隔板,隔板的两侧分别为 2 mol,0℃的单原子理想气体 A 及 5 mol,100℃的双原子理想气体 B,两气体的压力均为 100 kPa。活塞外的压力维持在 100 kPa 不变。今 将容器内的隔板撤去,使两种气体混合达到平衡态。求末态的温度 T 及过程的 。 解:过程图示如下 假定将绝热隔板换为导热隔板,达热平衡后,再移去隔板使其混合,则 由于外压恒定,求功是方便的

由于汽缸为绝热,因此 △U=R=-3696J △H=△+p∥-(Pa+PB】 =△U+RaT-Tu+1T1】 =-369.6+8.314×7x350.93-(2×273.15+5×373.15] =0灯 2.10已知水(0,1D在100℃的饱和蒸气压P=101325kPa,在此温度、压力下水的摩尔蒸发格 △,H。=40.668Wmol.求在在100℃,101.325kPa下使1kg水蒸气全部凝结成液体水时的 2,W,△U,△H。设水蒸气适用理想气体状态方程式。 解:该过程为可逆相变 103 △H=-月.=1804068=-257u 恒压,Q=△H=-2257k灯 W=-pepAV=-Pep .7=7883147315 103 p =172.2kJ △U=W+Q=-2257+172.2=-2085k灯 2.11已知水(H0,)在100℃的饱和蒸气压p=101.325kPa,在此温度、压力下水的摩尔蒸发培 A,H。=0.6S:m。试分别求算下列两过程的W,Q,△U和△H。(水蒸气可按理想气体处理) (1)在100℃,101.325kPa条件下,1kg水蒸发为水蒸气 (2)在恒定100℃的真空容器中,1kg水全部蒸发为水蒸气,并且水蒸气压力恰好为101.325kPa。 解:(1)题给过程的始末态和过程特性如下: n=m/M Ikg/18.015g:mor!=55.509mol H200) H20(g) 恒温恒乐 373.15K101325kP可逆相酸373.15K1o1325kP 题给相变焓数据的温度与上述相变过程温度一致,直接应用公式计算 Q,=△H=nA2Hm=n(△pHm)=2257k灯 W=-pambAV=-p(Vg-Vi)-pVg=-n:RT=-172.2kJ △U=Qp+W=2084.79J (2)真空容器中W=0kJ
由于汽缸为绝热,因此 2.10 已知水(H2O, l)在 100℃的饱和蒸气压 ,在此温度、压力下水的摩尔蒸发焓 。求在在 100℃,101.325 kPa 下使 1 kg 水蒸气全部凝结成液体水时的 。设水蒸气适用理想气体状态方程式。 解:该过程为可逆相变 2.11 已知水(H2O,l)在 100℃ 的饱和蒸 气压 p s =101.325kPa,在此 温度、压 力下水的 摩尔 蒸发焓 。试分别求算下列两过程的 W,Q,ΔU 和 ΔH。(水蒸气可按理想气体处理) (1)在 100℃,101.325kPa 条件下,1kg 水蒸发为水蒸气 (2)在恒定 100℃的真空容器中,1kg 水全部蒸发为水蒸气,并且水蒸气压力恰好为 101.325kPa。 解: (1)题给过程的始末态和过程特性如下: n = m/M = 1kg/18.015g·mol-1 = 55.509mol 题给相变焓数据的温度与上述相变过程温度一致,直接应用公式计算 n(ΔvapHm)=2257 kJ W=-pambΔV =-p(Vg -Vl)≈-pVg = -ng RT=-172.2kJ ΔU = Qp + W =2084.79kJ (2)真空容器中 W=0kJ

2.12已知100kPa下冰的熔点为0℃,此时冰的比熔化焓热Dh=33.3J·g.水和冰的平均 定压热容5分别为4134Jg'水'及200J%1水1。今在绝热容器内向1kg50℃的水中投入0.8 kg温度-20℃的冰。求: (1)末态的温度。 (2)末态水和冰的质量。 解:1kg50℃的水降温致0℃时放热 Q=m5,(water)DT=1000'4.184'50=209.2k灯 0.8kg-20℃的冰升温致0℃时所吸热 Q=%.8,Gce)DT=8002.00°20=32.0k灯 完全融化则需热 2=mxDh=800'333.3=266.64k灯 因此,只有部分冰熔化。所以系统末态的温度为0℃。设有mg的冰 熔化,则有 m (iceT.T )mh=mw(waterT-T) m(water TT(iceT) ①h =1004.18450.80020°20 333.3 =531.65g 系统冰和水的质量分别为 m%=800-.531.65=268.34g mm=1000+531.65=1531.65g
2.12 已知 100 kPa 下冰的熔点为 0 ℃,此时冰的比熔化焓热 J·g-1 . 水和冰的平均 定压热容 分别为 及 。今在绝热容器内向 1 kg 50 ℃的水中投入 0.8 kg 温度 -20 ℃的冰。求: (1)末态的温度。 (2)末态水和冰的质量。 解:1 kg 50 ℃的水降温致 0 ℃ 时放热 0.8 kg -20 ℃的冰升温致 0 ℃时所吸热 完全融化则需热 因此,只有部分冰熔化。所以系统末态的温度为 0 ℃。设有 g 的冰 熔化,则有 系统冰和水的质量分别为