
.,X,.,X。中来确定被测物理量的可靠值呢? =X一X南司 于是得到 Xa=X=lim Y (7 上式说明,在消除了系统误差之后,测定值的数学期望X等于被测物理量的真值X 这时测量结果 受偶然误差的影响 但是,在有限次测量 我们无法求得测定值的数学期望X。然而,在大多数场合下 可以用测定值的算术平均值X作为测量结果的可靠值。因为此时X远比各次测定的X值更 逼近于真值X。 显然,灭并不完全等于X,故我们希望知道这个可靠值灭的可靠程度如何,即灭与 X真究竞可能相差多大?按照误差定律,我们可以认为X真在绝大多数的情况下(概率为 99.7%)是落在 ±30 (8) 的范围内。式中。,称为平均值的标准误差。 (x,-) 0x=1 n(n-1) (9) 也就是说,我们以平均值标准误差的3倍作为有限次测量结果(可靠值灭)的可靠程 度。 实际应用(8)式来表示可靠值的可靠程度,有时嫌其麻烦。因为在物理化学实验中。 实际上测定某物理量的重复次数是很有限的:同时各次测量时实验条件的控制也并非完全相 同,故它的可靠程度比按误差理论得出的结果还要差一些。所以在物理化学实验数据的处理 中,常常将上式简化为: 若 n≥15 ±a (10) n≥5 则灭±173a 11) 式中 a=2x,-网 (12) 1- 称为平均误差。 式(10),(11)应用起来很方便,它表明了测量结果的可常程度。换言之,如果测定 重复了15次或更多,那么X值落在灭±a的范围内:如果重复测定的次数只有5次以上, 那么X值落在X士173a的范围内 3、测量的精密度 单次测量值X与可靠值灭的偏差程度称为测量的精密度。精密度一般常用三种不同方 式来表示 (1)用平均误差a表示。 (2)用标准误差σ表示: ∑(X,- n-1 (13) 6
6 据 X1,X2,X3,.,Xi,.,Xn 中来确定被测物理量的可靠值呢? 在只有偶然误差的测量中,假设系统误差已被消除,即 =X-X 真=0 于是得到 X 真=X= lim n X → (7) 上式说明,在消除了系统误差之后,测定值的数学期望 X等于被测物理量的真值 X 真 ,这时测量结果不受偶然误差的影响。 但是,在有限次测量时,我们无法求得测定值的数学期望 X。然而,在大多数场合下, 可以用测定值的算术平均值 X 作为测量结果的可靠值。因为此时 X 远比各次测定的 Xi 值更 逼近于真值 X 真。 显然, X 并不完全等于 X 真 ,故我们希望知道这个可靠值 X 的可靠程度如何,即 X 与 X 真 究竟可能相差多大?按照误差定律,我们可以认为 X 真 在绝大多数的情况下(概率为 99.7%)是落在 X X 3 (8) 的范围内。式中 X 称为平均值的标准误差。 X i i n X X n n = − − = ( ) ( ) 2 1 1 (9) 也就是说,我们以平均值标准误差的 3 倍作为有限次测量结果(可靠值 X )的可靠程 度。 实际应用(8)式来表示可靠值的可靠程度,有时嫌其麻烦。因为在物理化学实验中, 实际上测定某物理量的重复次数是很有限的;同时各次测量时实验条件的控制也并非完全相 同,故它的可靠程度比按误差理论得出的结果还要差一些。所以在物理化学实验数据的处理 中,常常将上式简化为: 若 n≥15 则 X a (10) 若 n≥5 则 X 1.73a (11) 式中 a n Xi X i n = − = 1 1 (12) 称为平均误差。 式(10),(11)应用起来很方便,它表明了测量结果的可靠程度。换言之,如果测定 重复了 15 次或更多,那么 X 真值落在 X a 的范围内;如果重复测定的次数只有 5 次以上, 那么 X 真值落在 X 1.73a 的范围内。 3、测量的精密度 单次测量值 Xi 与可靠值 X 的偏差程度称为测量的精密度。精密度一般常用三种不同方 式来表示。 (1)用平均误差 a 表示。 (2)用标准误差表示: = − − = ( X X ) n i i n 2 1 1 (13)
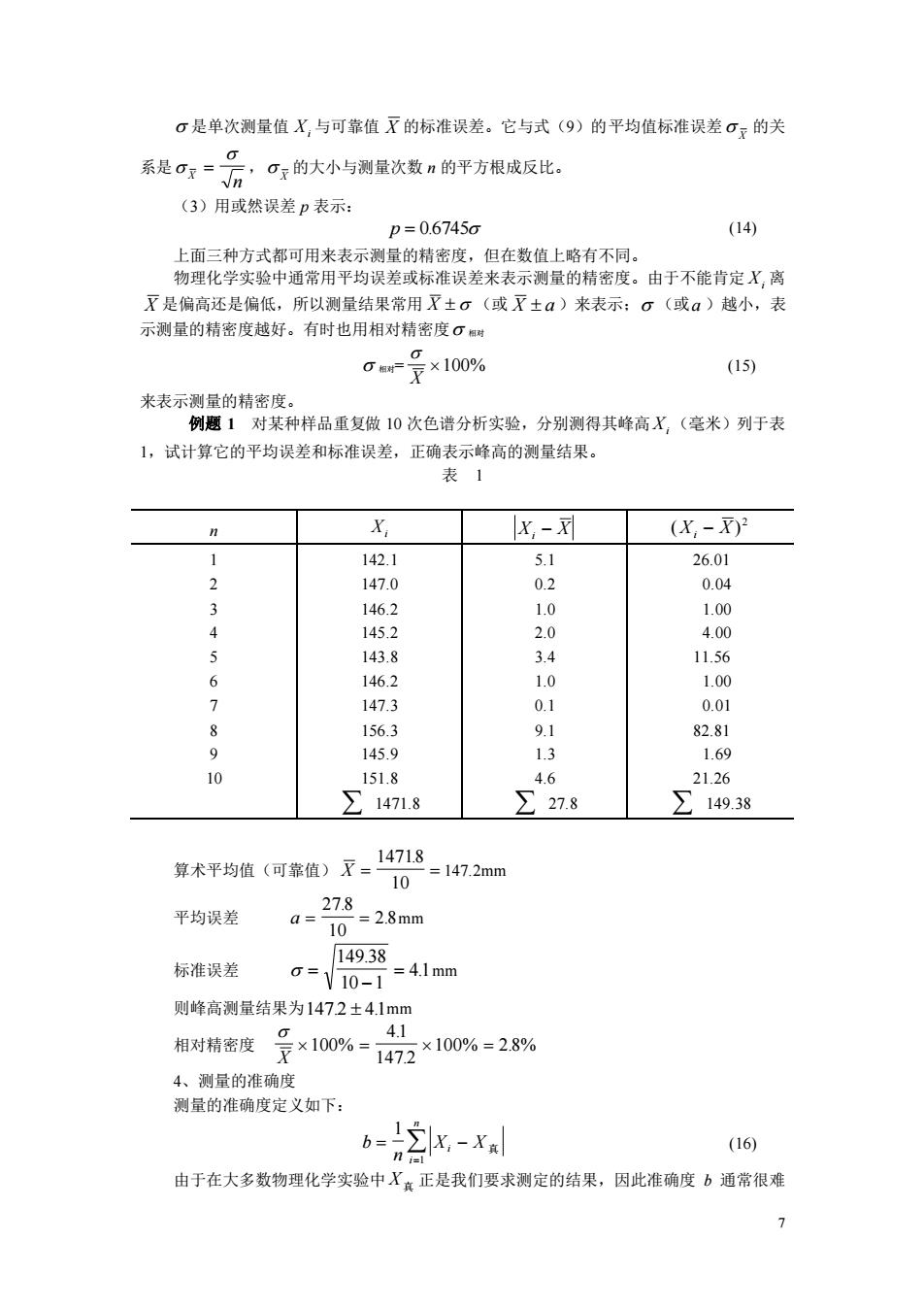
σ是单次测量值X,与可靠值X的标准误差。它与式(9)的平均值标准误差0,的关 系是0?=云,口的大小与测量次数n的平方根成反比· (3)用或然误差p表示: p=0.6745 (14) 上面三种方式都可用来表示测量的精密度,但在数值上略有不同。 物理化学实验中通常用平均误差或标准误差来表示测量的精密度。由于不能肯定X,离 灭是偏高还是偏低,所以测量结果常用又±。(或灭±a)来表示:。(或a)越小,表 示测量的精密度越好。有时也用相对精密度。 gr-景×10% (1) 米表示测量的精密度。 例题1对某种样品重复做10次色谱分析实验,分别测得其峰高X,(毫米)列于表 1,试计算它的平均误差和标准误差,正确表示峰高的测量结果。 表1 n X x,- (X,-)2 1 1421 26.01 147.0 0.04 146.2 1.0 1.00 145.2 2.0 4.00 5 143.8 34 11.56 6 146. 1.0 1.00 1473 0.01 156.3 9.1 82.81 9 145.9 1.3 1.69 10 1518 4.6 2126 ∑1471.8 ∑27.8 ∑14938 算术平均值(可靠值)了= 1471.8 10 =147.2mm 27 平均误差 a= 0=28mn 标准误差 149.38 0=10-1 =4.1mm 则峰高测量结果为1472±4.1mm 相对精密度是×10%=1472 4.1 ×100%=2.8% 4、测量的准确度 测量的准确度定义如下: 6=2x,-x (16) 由于在大多数物理化学实验中X。正是我们要求测定的结果,因此准确度b通常很难 1
7 是单次测量值 Xi 与可靠值 X 的标准误差。它与式(9)的平均值标准误差 X 的关 系是 X n = , X 的大小与测量次数 n 的平方根成反比。 (3)用或然误差 p 表示: p = 0.6745 (14) 上面三种方式都可用来表示测量的精密度,但在数值上略有不同。 物理化学实验中通常用平均误差或标准误差来表示测量的精密度。由于不能肯定 Xi 离 X 是偏高还是偏低,所以测量结果常用 X (或 X a )来表示; (或 a )越小,表 示测量的精密度越好。有时也用相对精密度 相对 相对= X 100% (15) 来表示测量的精密度。 例题 1 对某种样品重复做 10 次色谱分析实验,分别测得其峰高 Xi (毫米)列于表 1,试计算它的平均误差和标准误差,正确表示峰高的测量结果。 表 1 n Xi Xi − X (X X) i − 2 1 142.1 5.1 26.01 2 147.0 0.2 0.04 3 146.2 1.0 1.00 4 145.2 2.0 4.00 5 143.8 3.4 11.56 6 146.2 1.0 1.00 7 147.3 0.1 0.01 8 156.3 9.1 82.81 9 145.9 1.3 1.69 10 151.8 4.6 21.26 1471.8 27.8 149.38 算术平均值(可靠值) X = = 14718 10 . 147.2mm 平均误差 a = = 27 8 10 2 8 . . mm 标准误差 = − = 149 38 10 1 41 . . mm 则峰高测量结果为 147.2 4.1 mm 相对精密度 X 100% = = 41 147 2 100% 2 8% . . . 4、测量的准确度 测量的准确度定义如下: b n Xi X i n = − = 1 1 真 (16) 由于在大多数物理化学实验中 X 真 正是我们要求测定的结果,因此准确度 b 通常很难